This set of Complex Analysis Multiple Choice Questions & Answers (MCQs) focuses on “Regions in the Complex Plane”.
1. What is the shape of the region formed by the set of complex numbers z satisfying |z-ω|≤ α?
a) circle of radius ω
b) circle with center ω
c) disk of radius α
d) disk with center α
View Answer
Explanation: The equation |z-ω|≤ α implies that the distance of z from ω is less than or equal to α. This means that a disk is formed with center ω and radius α.
2. The complex number given by [(√3/2)+i/2]5+[(√3/2)-i/2]5 lies, on which of the following regions?
a) imaginary axis
b) real axis
c) first quadrant
d) fourth quadrant
View Answer
Explanation: Let z=[(√3/2)+i/2]5+[(√3/2)-i/2]5 and ω=[(√3/2)+i/2]5 ⇒ \(\overline{\omega}\)=[(√3/2)-i/2]5
⇒ z=ω+\(\overline{\omega}\) ⇒ z is real (sum of conjugates is real) ⇒ z lies on real axis.
3. Find the area of the region given by 11≤|z| ≤ 19.
a) 120π sq. units
b) 180π sq. units
c) 240π sq. units
d) 320π sq. units
View Answer
Explanation: The region formed is an annulus of inner radius 11 units and outer radius 19 units. Therefore, the required area=π(192–112)=240π.
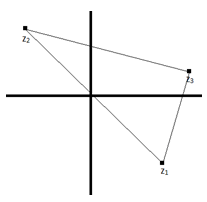
4. Find the largest angle of the triangle formed by thevertices z1=8(1-i), z2=8(i-1) and
Z3=10+2√7i.
a) π/3 radians
b) 2π/3 radians
c) π/2 radians
d) 3π/4 radians
View Answer
Explanation: Note that z1 and z2 are the opposite ends of a diameter of a circle of radius 8√2 units, centered at the origin. Also note that z3 lies on this circle (distance of z3 from origin = 8√2). Hence, angle corresponding to z3=π/2 radians.
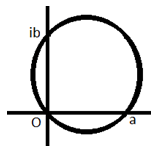
5. Find the equation of the circle passing through the origin and having intercepts a and b on real and imaginary axes, respectively, on the arg and plane.
a) zz̅=a(Im z)–b(Re z)
b) zz̅=a(Im z)+b(Re z)
c) zz̅=a(Re z)–b(Im z)
d) zz̅=a(Re z)+b(Im z)
View Answer
Explanation: Consider a point z on the circle. Therefore, arg [(z-a)/(z-ib)]=±π/2
⇒ (z-a)/(z-ib)+(z̅-a)/(z̅+ib)=0 ⇒ zz̅-a(z+z̅)/2–b(z-z̅)/2i=0
⇒ zz̅=a(Re z)+b(Im z).
6. On the arg and plane, the complex numbers z1, z2, z3, z4 are the vertices of a parallelogram. Evaluate (z4–z1+z2)/z3.
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: For a parallelogram, the diagonals bisect each other. Hence, their midpoints coincide.
This implies that (z1+z3)/2=(z2+z4)/2 ⇒ z1+z3=z2+ z4 ⇒ ( z4– z1+ z2)/ z3=1.
7. Consider the shape formed by the set of points z=ω-1/ω, where |ω|=2. Which of the following is incorrect?
a) eccentricity=4/5
b) |z|≤3
c) shape is an ellipse
d) major axis is of length=5/2
View Answer
Explanation: | ω|=2 ⇒ ω=2(cosθ+isinθ) ⇒ z=x+iy=2(cosθ+isinθ)-1/2(cosθ-isinθ)(⇒ |z|≤3)
=3/2cosθ+i5/2sinθ⇒x2/(3/2)2+y2/(5/2)2=1 ⇒ ellipse ⇒ e2=1-(9/4)/(25/4)=16/25
⇒ e=4/5.
8. Find the area enclosed by the curve formed by iz3+z2–z+i=0.
a) π/2
b) π
c) 3π/4
d) 2π
View Answer
Explanation: Dividing the equation by i on both sides, z3-iz2+iz+1=0
⇒ z2(z-i)+i(z-i)=0 ⇒ (z-i)(z2+i)=0 ⇒ z=i or z2=-i ⇒ |z|=|i|=1 or |z2|=|z|2=|-i|=1
⇒ |z|=1 ⇒ circle of radius 1 is formed. Hence, area=π(12)=π.
9. Given a vertex of the square circumscribing the circle |z-1|=√2 as 2+√3i, which of the following is not a vertex of this square ?
a) (1-√3)+i
b) –i√3
c) (√3+i)-i
d) i√3
View Answer
Explanation: The given circle has z0=1 as its center and √2 as radius. Let z1=2+i√3. Now, obtain z2 by rotating z1 anticlockwise by 900 about z0 ⇒ z2=(1-√3)+i. Now, z0 is midpoint of z1 and z3 and z2 and z4.
؞(z1+z3)/2 ⇒ (2+i√3+z3)/2=1 ⇒ z3=-i√3 and(z2+z4)/2=z0 ⇒ z4=(√3+i)-i.
10. Find the area of the region bounded by arg|z|≤π/4 and |z-1|<|z-3|.
a) 1 sq. units
b) 2 sq. units
c) 3 sq. units
d) 4 sq. units
View Answer
Explanation: |z-1|<|z-3| ⇒ (x-1)2+y2<(x-3)2+y2 ⇒ x<2.
Therefore, a triangle is formed with base length 4 and height 2 (along x-axis). Hence, the required area=1/2×4×2=4.
11. Find the locus of z/(1-z2), where z lies on the circle of radius 1 centered at origin and z≠±1.
a) line not passing through origin
b) |z|=√2
c) real axis
d) imaginary axis
View Answer
Explanation: Given |z|=1 and z≠±1, write ω=z/(1-z2)=z/(zz̅-z2)=1/(z̅-z).
Hence ω is a purely imaginary number and lies on imaginary axis.
12. Describe the region given by |z-i|z||-|z+i|z||=0.
a) real axis
b) imaginary axis
c) circle centered at origin
d) quadrant 2
View Answer
Explanation: |z/|z|-i|=|z/|z|+i|, z≠0 ⇒ z/|z| is unimodular complex number and lies on the perpendicular bisector of i and –i ⇒ z/|z|=±1 ⇒ z=±|z| ⇒ z is real.
13. The area of the region enclosed by the curve zz̅+a(z̅+z)+a=0 is 2π. If a2–7a+10=0, find the area of the region enclosed by the curve zz̅+2a(z̅+z)+a=0.
a) 4π sq. units
b) 10π sq. units
c) 14π sq. units
d) 22π sq. units
View Answer
Explanation: The curve represents a circle with center–a and radius (a2–a)1/2. Therefore, Area=π(a2–a)=2π ⇒ a=-1,2. Also, a2–7a+10=0 ⇒ a=2,5. Hence, a=2.
Hence required area=π(4a2–a)=14π.
14. Find the area of the region common to the sets S1={z∈C: |z|<4}, S2={z∈C:Im[(z-1+√3i)/(1-√3i)]>0} and S3={z∈C: Re z>0}.
a) 10π/3
b) 20π/3
c) 16π/3
d) 32π/3
View Answer
Explanation: S1: |z|<4, z lies inside the circle of radius 4; S2: √3x+y>0, z lies above the line √3x+y=0; S3: Re(z)>0, z lies to the right of the imaginary circle. Therefore, required area=π×42/4+π×42/6=20π/3.
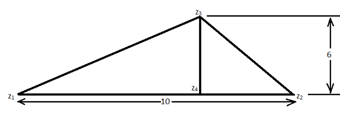
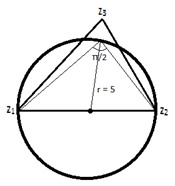
Find a possible value of z3 in terms of z1, z2 and z4.
a) z4+3/5(z2– z1)eiπ/2
b) z4-3/5(z2– z1)eiπ/2
c) z4+3/5(z2– z1)e-iπ/2
d) no such z3 is possible
View Answer
Explanation: If we draw a circle with z2-z1 as a diameter, we see that z3 would be outside the circle, since the radius of the circle is 5(<6). But we know that the points on the circle only would result in an angle of π/2. Hence, no such z3 is possible.
Sanfoundry Global Education & Learning Series – Complex Analysis.
To practice all areas of Complex Analysis, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Numerical Methods MCQ
- Check Engineering Mathematics Books
- Apply for 1st Year Engineering Internship
- Practice Probability and Statistics MCQ
