This set of Differential and Integral Calculus Multiple Choice Questions & Answers (MCQs) focuses on “Change of Order of Integration: Double Integral”.
1. Which of the following is not a property of double integration?
a) ∬ af(x,y)ds = a∬ f(x,y)ds, where a is a constant
b) ∬ (f(x,y)+g(x,y))ds = ∬f(x,y)ds+ ∬g(x,y)ds
c) \(∬_0^Df(x,y)ds = ∬_0^{D1}f(x,y)ds+ ∬_{D1}^{D2}f(x,y)ds,\) where D is union of disjoint domains D1 and D2
d) ∬(f(x,y)*g(x,y))ds = ∬f(x,y)ds*∬g(x,y)ds
View Answer
Explanation: The following are the properties of double integration:
- ∬af(x,y)ds = a∬f(x,y)ds
- ∬f(x,y)+g(x,y))ds = ∬f(x,y)ds+ ∬g(x,y)ds
- \(∬_0^Df(x,y)ds = ∬_0^{D1}f(x,y)ds+ ∬_{D1}^{D2}f(x,y)ds\)
2. The region bounded by circle is an example of regular domain.
a) False
b) True
View Answer
Explanation: A domain D in the XY plane bounded by a curve c is said to be regular in the Y direction, if straight lines passing through an interior point and parallel to Y axis meets c in two points A and B. Hence, region bounded by circle is an example of regular domain.
3. What is the result of the integration \(∫_3^4∫_1^2(x^2+y)dxdy\)?
a) \(\frac{83}{6} \)
b) \(\frac{83}{3} \)
c) \(\frac{82}{6} \)
d) \(\frac{81}{6} \)
View Answer
Explanation: Given: \(∫_3^4∫_1^2(x^2+y)dxdy\)
Integrating with respect to y first, we get,
\(∫_3^4(x^2(y)_1^2+(\frac{y^2}{2})_1^2)dx= ∫_3^4(x^2+\frac{3}{2}) dx\)
Next integrating with respect to x, we get,
\((\frac{x^3}{3})_3^4+\frac{3}{2}(x)_3^4= \frac{37}{3}+\frac{3}{2}=\frac{83}{6}\)
4. Volume of an object expressed in spherical coordinates is given by \(V = ∫_0^2π∫_0^\frac{π}{3}∫_0^1 r cos∅ \,dr \,d∅ \,dθ.\) The value of the integral is _______
a) \(\frac{√3}{2}\)
b) \(\frac{1}{√2} π\)
c) \(\frac{√3}{2}π\)
d) \(\frac{√3}{4} π\)
View Answer
Explanation: Given: \(V = ∫_0^2π∫_0^\frac{π}{3}∫_0^1 r cos∅ \,dr \,d∅ \,dθ.\)
\( V = ∫_0^2π∫_0^{\frac{π}{3}}(\frac{r^2}{2})_0^1 cos∅\, d∅\, dθ\)
\( V = \frac{1}{2} ∫_0^{2π}(sin∅)_0^\frac{π}{3} d∅ \,dθ\)
\(V = \frac{1}{2}×\frac{√3}{2} ∫_0^2π dθ\)
\( V = \frac{1}{2}×\frac{√3}{2} ×2π\)
\( V = \frac{√3}{2} π \)
5. Which of the following equation represents Moment of Inertia of a plane region relative to x-axis?
a) ∬x2 f(x,y)dxdy
b) ∬xf(x,y)dxdy
c) ∬y2 f(x,y)dxdy
d) ∬yf(x,y)dxdy
View Answer
Explanation: Moment of Inertia of a plane region,
Relative to x-axis is given by,
Ixx=∬y2 f(x,y)dxdy
Relative to y-axis is given by,
Iyy=∬x2 f(x,y)dxdy
6. What is the mass of the region R as shown in the figure?
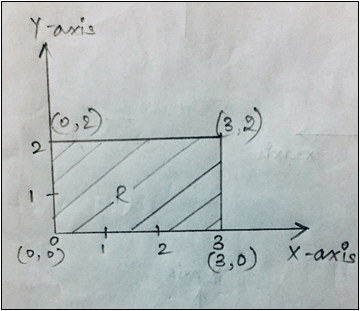
a) 8
b) 9
c) \(\frac{9}{2} \)
d) \(\frac{9}{4} \)
View Answer
Explanation: From the above figure, we can see that X-axis ranges from 0 to 3 and Y-axis ranges from 0 to 2.
Therefore, the mass of the region is given by,
\(M = ∫_0^2∫_0^3xy \,dx\,dy\)
\( = ∫_0^2y(\frac{x^2}{2})_0^3 dy = \frac{9}{2}(\frac{y^2}{2})_0^2 = 9 \)
7. The half-interval method in numerical analysis is also known as __________
a) Newton-Raphson method
b) Regula Falsi method
c) Taylor’s method
d) Bisection method
View Answer
Explanation: The Bisection method, also known as binary chopping or half-interval method, is a starting method which is used, where applicable, for few iterations, to obtain a good initial value.
8. Given \(∫_0^8x^\frac{1}{3}dx,\) find the error in approximating the integral using Simpson’s 1/3 Rule with n=4.
a) 1.8
b) 2.9
c) 0.3
d) 0.35
View Answer
Explanation: Given: \(∫_0^8x^\frac{1}{3}dx,n = 3,\)
Let \(f(x)= x^\frac{1}{3},\)
\(∆x = \frac{b-a}{2}= \frac{8-0}{2}=4\) ………………since b=8, a=0 (limits of the given integral)
Hence endpoints xi have coordinates {0, 2, 4, 6, 8}.
Calculating the function values at xi, we get,
\(f(0)= 0^\frac{1}{3}=0\)
\(f(2)= 2^\frac{1}{3}\)
\(f(4)= 4^\frac{1}{3}\)
\(f(6)= 6^\frac{1}{3}\)
\(f(8)= 8^\frac{1}{3} =2\)
Substituting these values in the formula,
\(∫_0^8x^\frac{1}{3} dx ≈ \frac{∆x}{3} [f(0)+4f(2)+2f(4)+4f(6)+f(8)]\)
\( ≈\frac{2}{3}[0+4(2^\frac{1}{3})+2(4^\frac{1}{3})+ 4(6^\frac{1}{3})+2] ≈ 11.65\)
Actual integral value,
\(∫_0^8x^\frac{1}{3} dx= \left(\frac{x^\frac{4}{3}}{\frac{4}{3}}\right)_0^8=12\)
Error in approximating the integral = 12 – 11.65 = 0.35
9. A sphere with the dimensions is shown in the figure. What is the error that can be incorporated in the radius such that the volume will not change more than 4%?
a) 0.127%
b) 0.0127%
c) 12.7%
d)1.27%
View Answer
Explanation: We know that volume of the sphere is,
\(V = \frac{4}{3} πR^3 \)
Differentiating the above equation with respect to R we get,
\(\frac{dV}{dR}= \frac{4}{3} π×3R^2=4πR^2\)
Since the volume of the sphere should not exceed more than 4%,
\(dR=\frac{dV}{4πR^2}=\frac{0.04}{4π(5)^2}=0.000127\)
Error in radius = 0.0127%
10. The x-coordinate of the center of gravity of a plane region is given by, \(x_c=\frac{1}{M}∬xf(x,y)dxdy.\)
a) True
b) False
View Answer
Explanation: The coordinates (xc,yc) of the centroid of a plane region with mass M is given by,
\(x_c=\frac{1}{M} ∬xf(x,y)dxdy\)
\(y_c=\frac{1}{M} ∬yf(x,y)dxdy\)
Sanfoundry Global Education & Learning Series – Differential and Integral Calculus.
To practice all areas of Differential and Integral Calculus, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for 1st Year Engineering Internship
- Check Engineering Mathematics Books
- Practice Numerical Methods MCQ
- Practice Probability and Statistics MCQ
