This set of Complex Mapping Multiple Choice Questions & Answers (MCQs) focuses on “Transformation w = ez“.
1. What is the region of the w plane into which the rectangular region in the Z plane bounded by the lines x = 0, y = 0, x = 1 and y = 2 is mapped under the transformation w = z + (2-i)?
a) Rectangle
b) Square
c) Triangle
d) Circle
View Answer
Explanation:
Given:w = z + (2-i)
i.e., u + iv = x + iy + (2-i) = (x+2) + i(y-1)
Equating the real and imaginary parts, u = x+2, v = y-1
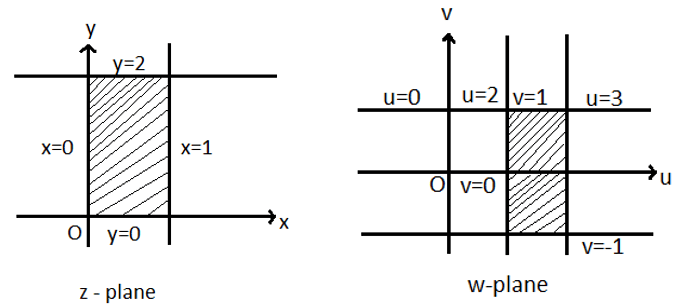
Given boundary lines are
x=0
y=0
x=1
y=2
Transformed boundary lines are
u= 0+2 = 2
v = 0-1 = -1
u= 1+2 = 3
v = 2-1 = 1
Hence, the lines x=0 y=0 x=1 and y=2 are mapped into the lines u=2, v=-1, u=3 and v=1 respectively which form a rectangle in the w plane.
2. Which of the following image of the circle |z| = 1 by the transformation w = z + 2 + 4i ?
a) Circle with centre (2, 4) and radius 1
b) Circle with centre (1, 4) and radius 2
c) Circle with centre (1, 4) and radius 3
d) Circle with centre (1, 3) and radius 4
View Answer
Explanation:
Given: w = z + 2 + 4i
i.e., u + iv = x + iy + 2 + 4i
= (x + 2) + i(y+4)
Equating the real and imaginary parts, we get
u = x+2, v = y+4
x = u-2, y = v-4
Given:|z| = 1
i.e., x2+y2 = 1
(u-2)2+(v-4)2 = 1
Hence, the circle x2+y2 = 1 is mapped into the (u-2)2+(v-4)2=1 in w plane which is also a circle with centre (2, 4) and radius 1.
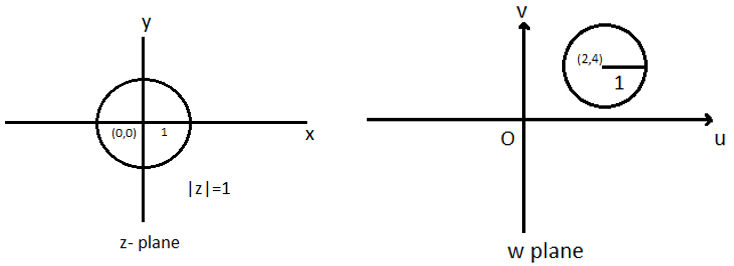
3. Which of the following transformations represents both magnification and rotation?
A) w = ez
b) w = cz
c) w = 1z
d) w = z2
View Answer
Explanation:
The transformation w = cz, where c is a complex constant, represents both magnification and rotation.
Let \(z = r\ e^{\text{iθ}}\) \( w = R\ e^{\text{iθ}}\)
and \( c = \alpha e^{\text{iα}}\)
Then Rei∅ \(= \left( \alpha e^{\text{iα}} \right)(re^{\text{iθ}})\)
\( = are^{i(\alpha + \theta)}\)
The transformation equations are
R=ar, ∅=θ+α
Thus, the point (r, θ) in the z-plane is mapped onto the point(ar, θ+α).
This means that the magnitude of the vector representing z is magnified by α=|c| and its direction is rotated through angleα=amp(c).
Hence, the transformation consists of a magnification and a rotation.
4. Which of the following regions of the w-plane into which the triangular region D enclosed by the lines x = 0,y = 0,x+y = 1 is transformation w = 2z?
a) u=0,v=0 and u+v=2
b) u=1, v=0 and u+v=1
c) u=0, v=1 and u+v=2
d)u=1, v=1 and u+v=1
View Answer
Explanation:
Let w = u + iv
z = x+iy
Given: w = 2z
u+iv = 2(x+iy)
u+iv = 2x+i 2y
u=2x →x=u/2, v=2y→y= v/2
In the z plane the line x = 0 is transformed into u = 0 in the w plane.
In the z plane the line y = 0 is transformed into v = 0 in the w plane.
In the z plane the line x+y = 1 is transformed into u+v = 2 in the w plane.
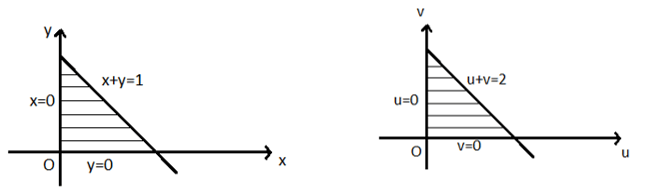
5. Which of the following is the image of the circle |z| = λ under the transformation w=5z?
a) |w| = z
b) |w| = 5z
c) |w| = 3z
d) |w| = 0
View Answer
Explanation:
Given: w = 5z
|w| = 5|z|
i.e., |w| = 5 [|z| = λ] Hence, the image of |z| = λ in z plane is transformed into |w| = 5 λ in the w plane under the transformation w = 5z.
6. Which of the following is the image of the circle |z| = 3 under the transformation w = 2z?
a) |w|= 2
b) |w|= 6
c) |w| = 3
d) |w| = 1
View Answer
Explanation:
Given: w=2z , |z|=3
|w| = (2)|z|
=(2)(3) , since |z| = 3
=6
Hence, the image of z= 3 in the |z| plane is transformed into |w| = 6 in the w plane under the transformation w = 2z.
7. Which of the following is an image of the region y>1 under the transformation w = (1-i)z?
a) u+v>1
b) u+v>0
c) u+v>2
d) u+v>3
View Answer
Explanation:
w = (1-i)z
u + iv = (1 – i)(x + iy)
=x + iy – ix + y
=(x+y)+ i(y-x)
i.e., u = x+y, v = y-x
u + v = 2y u – v = 2x
y = (u + v)/2 x = (u – v)/2
Hence, image region y > 1 is (u+v)/2 > 1 i.e., u + v > 2 in the w plane.
8. Which of the following image represents inversion under the transformation w = 1/z ?
a) Parabola
b) Rectangle
c) Circle
d) Hyperbola
View Answer
Explanation:
The transformation w = 1/z represents inversion with respect to the unit circle |z| = 1, followed by reflection in the real axis.
w = 1/z
(or) z = 1/w
\(x + iy = \frac{1}{u + iv}\)
\(x + iy = \frac{u – iv}{u^{2} + v^{2}}\)
\(x = \frac{u}{u^{2} + v^{2}} \ldots.(1)\)
\(y = \frac{- v}{u^{2} + v^{2}}\ldots.(2)\)
We know that, the general equation of circle in z plane is
x2 + y2 + 2gx + 2fy + c = 0 …(3)
Substitute (1) and (2) in (3) we get
\(\frac{u^{2}}{{(u^{2} + v^{2})}^{2}} + \frac{v^{2}}{{(u^{2} + v^{2})}^{2}} + 2g\ \left( \frac{u}{u^{2} + v^{2}} \right) + 2f\left( \frac{- v}{u^{2} + v^{2}} \right) + c = 0\)
i.e., c(u2+v2)+ 2gu – 2fv + 1 = 0…….(4)
which is the equation of circle in w plane.
9. Which of the following is the image of the circle |z| = 4 under the transformation w = 5z?
a) |w| = 20
b) |w| = 12
c) |w| = 9
d) |w| = 14
View Answer
Explanation:
Given: w = 5z ,|z| = 4
|w| = (5)|z|
=(5)(4) , since |z| = 4
=20
Hence, the image of |z| = 4 in the z plane is transformed into the |w| = 20 in the w plane under the transformation w = 5z.
10. Which of the following is a correct statement about conformal mapping?
a) A mapping w=f(z) is said to be conformal at z = z0, if f'(z0) ≠0
b) A mapping w=f(z) is said to be conformal at z = z0, if f'(z0) = 0
c) A mapping w=f(z) is said to be conformal at z = z0, if f'(z0) ≠1
d) A mapping w=f(z) is said to be conformal at z = z0, if f'(z0) =1
View Answer
Explanation:
In general linear transformation w = az+b where a and b are complex constants, represents magnification, rotation and translation.
A transformation under which angles between every pair of curves through a point are preserved in magnitude, but altered in sense is said to be an isogonal at that point.
A mapping w = f(z) is said to be conformal at z = z0, if f'(z0) ≠0.
11. Which of the following is known as the point, at which the mapping w = f(z) is not conformal i.e., f(z) = 0?
a) Critical point
b) Fixed point
c) Conformal point
d) Invariant point
View Answer
Explanation:
The point, at which the mapping w = f(z) is not conformal, i.e., f(z) = 0 is called a critical point of the mapping. If the transformation w = f(z) is conformal at a point, the inverse transformation z = f-1(w) is also conformal at the corresponding point. The critical points of z = f-1(w) are given by dz/dw=0.
12. Which of the following points is mapped onto themselves are ‘kept fixed’ under the mapping?
a) Invariant point
b) Critical point
c) Conformal point
d) Transformation point
View Answer
Explanation: Fixed or Invariant point of a mapping w = f(z) are points that are mapped onto themselves, are ‘kept fixed’ under the mapping. Thus they are obtained from w = f(z) = z. The identity mapping w = z has every point as a fixed point. The mapping w = z has infinitely many fixed
13. Which of the following are the critical points of the transformation w2 = (z-α)(z-β)?
a) \(\frac{\alpha + \beta}{2},\) α and β
b) 0
c) 1
d) ∞, -∞
View Answer
Explanation:
Given: w2 = (z-α)(z-β) ….(1)
Critical points occur at dw/dz = 0 and dz/dw = 0
Differentiating (1) with respect to z, we get
\(2w\ \frac{\text{dw}}{\text{dz}} = (z – \alpha) + (z – \beta)\)
\( = 2z – (\alpha + \beta)\ldots(2)\)
\(\frac{\text{dw}}{\text{dz}} = \frac{2z – (\alpha + \beta)}{2w}\ldots(3)\)
Case(i) \(\frac{\text{dw}}{\text{dz}} = 0 \rightarrow \ \frac{2z – (\alpha + \beta)}{2w} = 0\)
\(2z – (\alpha + \beta) = 0\)
\(2z = \ \alpha + \beta\)
\(z = \ \frac{\alpha + \beta}{2}\ \)
Case (ii) \( \frac{\text{dz}}{\text{dw}} = 0\ \ \ \rightarrow \ \frac{2w}{2z – (\alpha + \beta)} = 0\ \rightarrow \ \frac{w}{z – \frac{\alpha + \beta}{2}} = 0\)
w = 0 → (z-α)(z-β) = 0
z = α, β
14. Which of the following is the critical point of the
transformation\(w = z^{2} + \frac{1}{z^{2}}\)?
a) ±1, ±i, 0
b) ±∞
c) ± i
d) 0
View Answer
Explanation:
Given: \(w = \ z^{2} + \frac{1}{z^{2}}\ldots(1)\)
Critical points occur at dw/dz = 0 and dz/dw = 0
Differentiating 1 w.r.t z, we get,
\(\frac{\text{dw}}{\text{dz}} = 2z – \frac{2}{z^{2}} – \frac{2z^{4} – 2}{z^{3}}\)
Case(i) \( \frac{\text{dw}}{\text{dz}} = 0 \rightarrow \frac{2z^{4} – 2}{z^{3}} = 0 \rightarrow 2z^{4} – 2 = 0\)
z4 – 1 = 0
z = ±1 ,±i
Case(ii) \( \frac{\text{dz}}{\text{dw}} = 0 \rightarrow \ \frac{z^{3}}{2z^{4} – 2} = 0 \rightarrow \ z^{3} = 0 \rightarrow z = 0\)
The critical points are ±1, ±i, 0
15. Which of the following is the critical point of the transformation w = z + 1/z?
A) 0, ±1
b) ±1
c) ±∞
d) ±i
View Answer
Explanation:
Given: w = z + 1/z …(1)
Critical points occur at dw/dz = 0 and dz/dw = 0
Differentiating (1) w.r.t z, we get
\(\frac{\text{dw}}{\text{dz}} = 1 – \frac{1}{z^{2}} = \ \frac{z^{2} – 1}{z^{2}}\)
Case(i) \(\frac{\text{dw}}{\text{dz}} = 0 \rightarrow \frac{z^{2} – 1}{z^{2}\ } = 0 \rightarrow \ z^{2} – 1 = 0 \rightarrow z = \pm 1 \)
Case(ii) \( \frac{\text{dz}}{\text{dw}} = 0 \rightarrow \frac{z^{2}}{z^{2} – 1} = 0 \rightarrow \ z^{2} = 0 \rightarrow z = 0\)
The critical points are 0, ±1.
Sanfoundry Global Education & Learning Series – Complex Mapping.
To practice all areas of Complex Mapping, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Engineering Mathematics Books
- Practice Numerical Methods MCQ
- Apply for 1st Year Engineering Internship
- Practice Probability and Statistics MCQ
