This set of Differential and Integral Calculus Multiple Choice Questions & Answers (MCQs) focuses on “Curves in Cartesian Form”.
1. Which of the following characteristic is not included in the study of general procedure for tracing the algebraic curve?
a) Symmetry
b) Region or Extent
c) Orthogonality
d) Tangents to the Curve at the origin
View Answer
Explanation: General procedure for tracing the algebraic curve consists of the study of the following characteristics of the curve:
- Symmetry
- Region/Extent
- Asymptotes
- Origin
- Tangents to the curve at the origin
- Maxima and Minima
- Sign of the first derivative
- Sign of the second derivative
- Inflection Point
2. Which of the following is the representation of a plane algebraic curve of nth degree?
a) f(x,y)=ayn+(bx+c) yn-1+(dx2+ex+f) yn-2+⋯+un (x)=0
b) f(x,y)=ayn-1+(bx+c) yn-2+(dx2+ex+f) yn-3+⋯+un (x)=0
c) f(x,y)=ayn+byn-1+cyn-2+⋯+un (x)=0
d) f(x,y)=ayn+(bx+c) yn+(dx2+ex+f) yn+⋯+un (x)=0
View Answer
Explanation: Plane algebraic curve of nth degree is represented by,
f(x,y)=ayn+(bx+c) yn-1+(dx2+ex+f) yn-2+⋯+un (x)=0
Where a, b, c, d, e, f are all constants and un(x) is a polynomial in x of degree n.
3. If f(x,y)=ayn+(bx+c) yn-1+(dx2+ex+f) yn-2+⋯+un(x)=0…(1), is the algebraic curve of nth order then, what is the condition for the curve to be symmetric about x-axis?
a) Only even powers of x appear in (1)
b) Only odd powers of x appear in (1)
c) Only odd powers of y appear in (1)
d) Only even powers of y appear in (1)
View Answer
Explanation: If only even powers of y occur in (1), i.e., if y is replaced by -y in (1), the equation (1) remains unaltered or in other words f(x, -y) = f(x, y).
4. Which of the following is not an example for curve symmetric about y axis?
a) x2=4ay
b) x2=ay
c) y2=4ax
d) x2=2ay
View Answer
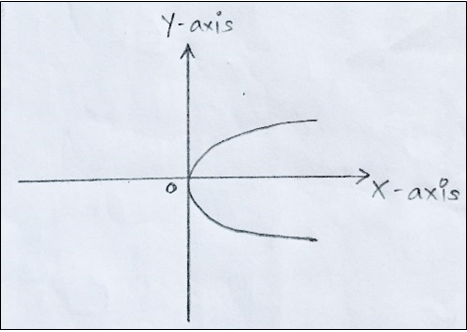
Explanation: Out of the given options, y2=4ax is an example of curve symmetric about x axis and not about y axis as shown in the figure below,
5. Which of the following graphs represent symmetric about the origin?
a) y2=4ax
b) x5+y5=5a2x2y
c) x2=4ay
d) x2+y2=a2
View Answer
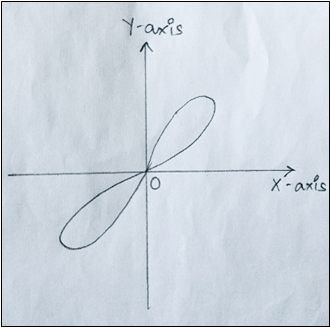
Explanation: Out of the given options, x5+y5=5a2 x2 y represents the curve symmetric about the origin and can be observed as,
6. What are the tangents to the curve x3+ y3=3axy at the origin?
a) x=0
b) x=0, y=0
c) y=0
d) x=y
View Answer
Explanation: Given: x3+ y3=3axy
To find the tangent to the curve at the origin, we need to equate the lowest degree term to 0.
Therefore, 3axy=0, which gives x=0 and y=0 as two tangents to the curve at origin.
7. At the point where \(\frac{dy}{dx}=0,\) the tangent is parallel to y axis.
a) False
b) True
View Answer
Explanation: At the point where \(\frac{dy}{dx}=0,\) the tangent is parallel to x axis, i.e., horizontal. At the point where \(\frac{dy}{dx}=∞,\) the tangent is vertical, i.e., parallel to y axis.
8. Which of the following is not correct regarding signs of derivatives?
a) If \(\frac{dy}{dx}>0,\) then the curve is increasing in [a, b]
b) If \(\frac{dy}{dx}<0,\) then the curve is increasing in [a, b]
c) If \(\frac{d^2 x}{dy^2}>0, \) then curve is convex and concave upward (holds water)
d) If \(\frac{d^2 x}{dy^2}>0, \) then curve is concave downward (spills water)
View Answer
Explanation: In an interval, a≤x≤b,
- If \(\frac{dy}{dx}>0, \) then the curve is increasing in [a, b]
- If \(\frac{dy}{dx}< 0, \) then the curve is increasing in [a, b]
- If \(\frac{d^2x}{dy^2}>0, \) then curve is convex and concave upward (holds water)
- If \(\frac{d^2x}{dy^2}>0, \) then curve is concave downward (spills water)
9. What is the value of the given limit, \(\lim_{x\to 0}\frac{25}{x}\)?
a) 25
b) 0
c) \(\frac{1}{2} \)
d) \(\frac{3}{2} \)
View Answer
Explanation: Given: \(\lim_{x\to 0}\frac{25}{x}\)
Using L’Hospital’s Rule, by differentiating both the numerator and denominator with respect to x,
\(\lim_{x\to 0}\frac{25}{x}= 25.\)
10. Oblique asymptotes are parallel to both x and y axes.
a) True
b) False
View Answer
Explanation: Oblique asymptotes are those which are neither parallel to x-axis nor y-axis and are given by y=mx+c where \(m=\lim_{x\to ∞}(\frac{x}{y})=\lim_{x\to ∞}(y-mx).\)
Sanfoundry Global Education & Learning Series – Differential and Integral Calculus.
To practice all areas of Differential and Integral Calculus, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Engineering Mathematics Books
- Apply for 1st Year Engineering Internship
- Practice Probability and Statistics MCQ
- Practice Numerical Methods MCQ
