Cauchy's Integral Formula Questions and Answers

This set of Complex Integration Multiple Choice Questions & Answers (MCQs) focuses on “Cauchy’s Integral Formula”.

1. Which of the following is obtained by evaluating \(∫_C\frac{z}{z-3}dz\), where C is |z|=4 ?
a) 2πi
b) 6πi
c) 8πi
d) Πi
View Answer

Answer: b
Explanation: We know that, Cauchy’s Integral Formula is
\(∫_C\frac{f(z)}{z-a}dz=2 π i f(a)\) —————— (1)
Given: f (z) = z, a=3, C is |z| = 4
Since a=3 lies inside |z| = 4, then f (a) = f (3) = 3

From (1) \(∫_C\frac{z}{z-3}dz=2πi[3]=6πi\)

2. Which of the following values is obtained by evaluating \(∫_C\frac{dz}{ze^z}\), where C is |z| =1?
a) 0
b) 2π
c) 2πi
d) 4πi
View Answer

Answer: c
Explanation: Cauchy’s Integral formula is written as
\(∫_C\frac{f(z)}{z-a}dz=2 π i f(a) \)
Given: \(∫_C\frac{dz}{ze^z}=∫_C\frac{e^{-z}}{z-0} \)
Here, f (z) = e^-z; a=0 lies inside |z| = 1

So, f(a) = f(0) = e^-0= 1
From (1),
\(∫_C\frac{e^{-z}}{z}dz\)= 2πif(0)=2πi(1)=2πi

3. Using Cauchy’s Integral Formula, which of the following values can be obtained by evaluating \(∫_C\frac{dz}{z^2e^z}\), where C is |z|=1?
A) -2πi
b) 2πi
c) 4π
d) 0
View Answer

Answer: a
Explanation: Cauchy’s Integral formula is written as
\( ∫_C \frac{f(z)}{(z-a)^{n+1}}dz= \frac{2 π i}{n!}f^n(a)\) ——- (1)
Given:\(∫_C\frac{dz}{z^2e^z}= ∫_C\frac{e^{-z}dz}{z^2}= ∫_C\frac{e^{-z}}{(z-0)^2}\)
Here, f (z) = e^-z; a=0 lies inside |z| = 1
From (1),
\(∫_C\frac{e^{-z}}{z^2}dz= \frac{2πi}{1!}f'(0)\)
To find f’ (0), f (z) = e^-z
f’(z) = -e^-z
f’(0) = -e^-0= -1
\(∫_C\frac{e^{-z}}{z^2}dz = 2 π i (-1) = -2πi\)

4. Which of the following can be obtained by evaluating \(∫_C\frac{zdz}{(z-1)^3}\), where C is |z|=2?
a) 1
b) 0
c) -1
d) 2
View Answer

Answer: b
Explanation: Cauchy’s Integral Formula is
\( ∫_C\frac{f(z)}{(z-a)^{n+1}}dz= \frac{2 π i}{n!}f^n (a) ———– (1)\)
Given:\(∫_C\frac{zdz}{(z-1)^3}\)
Here, f (z) = z; a=1 lies inside |z| = 2
From (1), \(∫_C\frac{zdz}{(z-1)^3}=\frac{2 π i}{2!}f”(1)\)
f(z)= z; f'(z)= 1
f”(z)= 0; f”(1)= 0
\(∫_C\frac{zdz}{(z-1)^3} = π i [0] = 0 \)

5. Which of the following can be obtained by evaluating \(∫_Cz^2e^{1/z}dz \), where C is |z| = 1?
a) 1
b) 0
c) -1
d) ∞
View Answer

Answer: b
Explanation: Given that \( ∫_C z^2e^{1/z}dz= ∫_C \frac{z^2}{e^{1/z}}dz\)
Z=0 e^-1/0= e^-∞=0
Z =0 lies inside |z| = 1
Cauchy’s integral formula is \( ∫_C\frac{f(z)}{z-a}dz=2 π i f(a)\)
\(∫_C\frac{z^2}{e^{-1/z}}dz=2 π i f(0)=0 \)

Subscribe Now: Engineering Mathematics Newsletter | Important Subjects Newsletters

6. Which of the following can be obtained by evaluating \(∫_C\frac{cos⁡πz^2}{(z-1)(z-2)}dz, \) where C is |z|= 3/2?
a) 4πi
b) 2πi
c) 0
d) 1
View Answer

Answer: b
Explanation:
Given: \( \frac{cos⁡πz^2}{(z-1)(z-2)}dz, \) where C is |z|= 3/2
We can rewrite the function as
\(∫_C\frac{[\frac{cos⁡πz^2}{z-2}]}{z-1}dz \) From the above expression, it is understood that z = 2 lies outside |z| = 3/2

Here, \( f(z) = \frac{cos⁡πz^2}{(z-2)} \)
z = 1 lies inside |z| = 3/2, \( f(1)= cos⁡π/(1-2) = 1 \)
\( ∫_C\frac{\frac{cos⁡πz^2}{z-2}}{z-1}dz=2 π i f(1)= 2 π i(1)= 2πi \)

7. Which of the following can be obtained by evaluating \(∫_C\frac{z^2}{(z-1)^2 (z+2)}dz, \) where C is |z|=3?
a) 8πi
b) ±i
c) 2πi
d) 4πi
View Answer

Answer: c
Explanation: z =1 and z=-2 lies inside |z| = 3
By Partial fractions,
\( \frac{z^2}{(z-1)^2(z+2)}=\frac{A}{(z-1)} + \frac{B}{(z-1)^2} + \frac{c}{(z+2)} \)
z²=A(z-1)(z+2)+ B(z+2)+C(z-1)²
Solving the above expression, we get A= 5/9, B= 1/3, C= 4/9
Substituting the values,
\( \frac{z^2}{(z-1)^2(z+2)}= \frac{\frac{5}{9}}{(z-1)} + \frac{\frac{1}{3}}{(z-1)^2} + \frac{\frac{4}{9}}{z+2} \)
\( ∫_C\frac{z^2}{(z-1)(z+2)}dz = ∫_C\frac{5/9}{z-1}dz + \frac{1}{3}∫_C\frac{1}{(z-1)^2}dz+ \frac{4}{9}∫_C\frac{1}{(z+2)}dz \)
Applying Cauchy’s Integral Formula,
\( = \frac{5}{9}2πif(1)+ \frac{1}{3} 2πif'(1)+ \frac{4}{9}2πif(-2) \)
\( = \frac{5}{9} 2πi(1)+ \frac{1}{3} 2πi(0) + \frac{4}{9} 2πi(1)\)
\( = 2πi[\frac{5}{9}+\frac{4}{9}]= 2πi\)

8. Which of the following can be obtained by evaluating \(∫_C\frac{(7z-1)}{z^2-3z-4} dz, \) where C is ellipse x²+9y²=9?
a) \( \frac{8}{5} πi \)
b) \( \frac{16}{5} πi \)
c) \( \frac{9}{2} πi \)
d) \( \frac{7}{5} πi \)
View Answer

Answer: b
Explanation: Cauchy’s Integral Formula is \(∫_C\frac{(f(z)}{z-a}dz=2 π i f(a)\)
Given: \(∫_C\frac{(7z-1)}{z^2-3z-4} dz, \) where C is ellipse x²+9y²=9
\( \frac{x^2}{3^2} + \frac{y^2}{1^2}=1 \)
\( ∫_C\frac{(7z-1)}{(z^2-3z-4)}dz= ∫_C\frac{(7z-1)}{(z-4)(z+1)}dz \)
This can be rewritten as \(∫_C\frac{\frac{(7z-1)}{(z-4)}}{z+1}dz \)
It is understood that z=4 lies outside C, which is represented below.

Here, \(f(z) = \frac{7z-1}{z-4} \)
We observe that z= -1 lies inside C, \( f (-1) = \frac{-7-1)}{-1-4}= \frac{-8}{-5}= \frac{ 8}{5} \)
\(∫_C\frac{\frac{(7z-1)}{(z-4)}}{z+1}dz = 2 π i(8/5) = \frac{16}{5} π i \)

9. Using Cauchy’s Integral, which of the following can be obtained by evaluating \(∫_C\frac{z}{(z-1)^2(z+2)}dz, \) where C is the circle |z-2|=2?
a) \(\frac{5}{9} πi \)
b) \(\frac{8}{9} πi \)
c) \(\frac{11}{9} πi \)
d) \(\frac{10}{9} πi \)
View Answer

Answer: d
Explanation: Given |z-2| = 2
Here, centre is 2, radius is 2
We observe that z=1 lies inside C: |z-2| =2
Z=-2 lies outside C: |z-2| =2
\(∫_C\frac{z^2}{(z-1)^2 (z+2)} dz= ∫_C\frac{\frac{z^2}{z+2}}{(z-1)^2}dz \)
Here, \(f (z) = \frac{z^2}{z+2} \) is analytic inside C.
Hence, by Cauchy’s Integral Formula,
\(∫_C\frac{f(z)}{(z-a)^2} dz=2πif'(a) = 2πif'(1) \)
To find f’(1),
Given that \(f (z) = \frac{z^2}{z+2} \)
Differentiating, \(f’(z) = \frac{(z+2)(2z)- z^2 (1)}{(z+2)^2} \)
We get \( f’ (1) = \frac{6-1}{9} = \frac{5}{9} \)
\(∫_C\frac{z^2}{(z+2)(z-1)^2} dz=2πi\frac{5}{9}= \frac{10}{9} π i \)

10. Which of the following can be obtained by calculating \(∫_C\frac{1}{z^2-1}dz,\) where C is the circle with centre at z=0 and radius 3?
a) 4πi
b) 2πi
c) -1
d) 0
View Answer

Answer: d
Explanation:
Cauchy’s Integral Formula is \(∫_C\frac{f(z)}{z-a}dz=2 π i f(a)\)
Given: \(∫_C\frac{f(z)}{(z^2-1)}dz,\) where C is |z|=3
\( ∫_C\frac{1}{z^2-1}dz= ∫_C\frac{1}{(z+1)(z-1)} dz \)
Here, f (z) = 1
We observe that z=1 lies inside |z| = 3, f (1) = 1 and
z=-1 lies inside |z| = 3, f (-1) = 1
Consider \( \frac{1}{(z+1)(z-1)} \)
By Partial Fractions,
\(∫_C\frac{1}{(z+1)(z-1)} dz= \frac{1}{2} ∫_C\frac{1}{(z-1)}dz- \frac{1}{2}∫_C\frac{1}{(z+1)}dz \)
= \( \frac{1}{2} ∫_C\frac{1}{(z-1)}dz- \frac{1}{2}∫_C\frac{1}{(z-(-1))} dz \)

= \( \frac{1}{2} 2πi f(1)- \frac{1}{2} 2πi f(-1) \)
= π i (1) – π i (1) = 0

11. Which of the following can be obtained by calculating \(∫_C\frac{sin⁡πz^2+cos⁡π z^2}{(z-1)(z-2)} dz, \) where C is |z|=4?
a) 2πi
b) 4πi
c) 0
d) 1
View Answer

Answer: b
Explanation:
Cauchy’s Integral Formula is \(∫_C\frac{f(z)}{z-a}dz=2 π i f(a)\)
Given:\( ∫_C\frac{sin⁡π z^2+cos⁡π z^2}{(z-1)(z-2)}dz, \)where C is |z|=4
Here, f(z) = sin π z² + cos π z²
We observe that z=1 lies inside |z|=4, f (1) = sin π + cos π = 0 – 1 = -1 and
z =2 lies inside |z|=4, f (2) = sin 4π + cos 4π = 0 + 1 = 1
Consider \(\frac{1}{(z-1)(z-2)} \)
By Partial Fractions,
\( \frac{1}{(z-1)(z-2))}= \frac{1}{(z-2)}- \frac{1}{(z-1)} \)
Therefore,
\(∫_C\frac{sin⁡π z^2+cos⁡π z^2}{(z-1)(z-2)}dz= ∫_C\frac{sin⁡π z^2+cos⁡π z^2}{(z-2)} dz- ∫_C\frac{sin⁡π z^2+cos⁡π z^2}{(z-1)}dz \)
= 2 π i f (2) – 2 π i f (1)
= 2 π i (1) – 2 π i (-1)
= 2 π i + 2 π i = 4 π i

12. Which of the following can be obtained by calculating \(∫_C\frac{(z+1)}{(z-4)(z-2)}dz, \) where C is the circle |z|=3?
a) 2 π i
b) -2 π i
c) \(\frac{4}{3} π i\)
d) \(-\frac{4}{3} π i\)
View Answer

Answer: b
Explanation:
Given that |z| = 3
Center is 0 and Radius is 3
Therefore, z=4 lies outside |z| = 3; z=2 lies inside |z| =3
\(∫_C\frac{(z+1)}{(z-4)(z-2)} dz= ∫_C\frac{(\frac{z+1}{z-4})}{z-2}dz \)
Here, \( f (z) = \frac{(z+1)}{(z-4)}\) is analytic inside C.
Hence, by Cauchy’s Integral Formula, \(∫_C\frac{f(z)}{z-a}dz=2 π i f(a)\)
Therefore, \( f (z) = \frac{(z+1)}{(z-4)}; f (1) = \frac{(1+1)}{(1-4)}=\frac{-2}{3}\)
\(∫_C\frac{(z+1)}{(z-4)(z-2)} dz= 2 π i (\frac{-2}{3})= -\frac{4}{3} πi \)

13. Which of the following can be obtained by \(∫_C\frac{(z^2+1)}{(z^2-1)} dz, \) where C is |z-3|=3?
a) 4 π i
b) 8 π i
c) 12 π i
d) 2 π i
View Answer

Answer: d
Explanation:
Cauchy’s Integral Formula is \(∫_C\frac{f(z)}{z-a}dz=2 π i f(a)\)
Given: |z-3| =3 is a circle, whose centre is 3 and radius is 3.
\(∫_C\frac{(z^2+1)}{(z^2-1)}dz= ∫_C\frac{(z^2+1)}{(z-1)(z+1)}dz= ∫_C\frac{(\frac{z^2+ 1}{z+1})}{(z-1)}dz \)

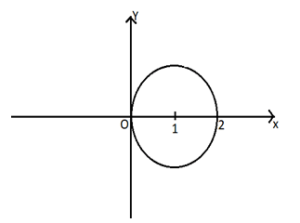
We observe that z=-1 lies outside C.
Here, \(f (z) = \frac{(z^2+1)}{(z+1)} \)
From the above figure, we observe that z=1 lies inside C, \(f (1) = \frac{(1+1)}{(1+1)}=1 \)
\(∫_C\frac{(\frac{z^2+ 1}{z+1})}{(z-1)}dz=2 π i f(1)= 2 π i(1)= 2πi \)

14. Which of the following can be obtained by evaluating \(∫_C\frac{(z+1)}{(z^2+ 2z+4)}dz\) where C is the circle |z+1+i|=3?
a) 2 π i
b) 4 π i
c) 8 π i
d) π i
View Answer

Answer: d
Explanation:
Given: |z+1+i| = 3
That is |z-[-(1+i)] = 3 is a circle, whose centre is (-1, -1) and radius is 3.
Now, consider z² + 2z + 4= [z—(-1+i√3) z—(-1-i√3] -1+i√3, which means (-1,√3) lies outside C.
-1-i√3, which means (-1,-√3) lies inside C.
\(∫_C\frac{(z+1)}{(z^2+2z+4)}dz= ∫_C\frac{\frac{(z+1)}{[z-(-1+i√3)]}}{[z-(-1-i√3)]}dz\)
Here, \(f (z) =\frac{(z+1)}{z-(-1+i√3)}\) is analytic inside C
Hence, by Cauchy’s Integral Formula,
\(∫_C\frac{f(z)}{z-a}dz=2 π i f(a)\)
\(∫_C\frac{(z+1)}{(z^2+2z+4)} dz= 2 π i f(-1-√3 i) \)
\( = 2 π i \frac{(-1-√3 i+1)}{(-1-√3i+1-i√3)}= 2πi[\frac{(-√3 i)}{(-2√3 i)}]=πi \)

15. If a function f(z) is analytic within and on a simple closed curve C and ‘a’ is any point lying in it,
then \(f’ (a) = \frac{1}{(2 π i)} ∫_C\frac{f(z)}{(z-a)^2} dz = ? \)
a) True
b) False
View Answer

Answer: a
Explanation:
Cauchy’s Integral Formula is \(∫_C\frac{f(z)}{z-a}dz=2 π i f(a)\)
Differentiating with respect to ‘a’,
\(f’ (a)= \frac{d}{da} [\frac{1}{2πi} ∫_C\frac{f(z)}{(z-a)}dz]= \frac{1}{2πi}∫_C\frac{∂}{∂a} (\frac{f(z)}{(z-a)})dz \)
\( f^(a)= \frac{1}{2πi}∫_Cf(z)\frac{∂}{∂a}(\frac{1}{z-a})dz= \frac{1}{2 π i} ∫_Cf(z)[\frac{-1}{(z-a)^2}(-1)]dz \)
\( = \frac{1}{2πi}∫_Cf(z)\frac{1}{(z-a)^2}dz = \frac{1}{2πi} ∫_C\frac{f(z)}{(z-a)^2}dz. \)

Sanfoundry Global Education & Learning Series – Complex Integration.

To practice all areas of Complex Integration, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Complex Integration Questions and Answers – Cauchy’s Integral Theorem

» Next - Complex Integration Questions and Answers – Taylor’s Series

Related Posts:

Practice Numerical Methods MCQ
Check Engineering Mathematics Books
Apply for 1st Year Engineering Internship
Practice Probability and Statistics MCQ

Recommended Articles: