This set of Engineering Mathematics Multiple Choice Questions & Answers (MCQs) focuses on “Functional Dependence”.
1. What is the meaning of functional dependence in partial differentiation, when ‘u’ is a function of (x,y) and ‘v’ is also a function of (x,y)?
a) \(\frac {∂ (u,v)}{∂(x,y)}\) = 0
b) \(\frac {∂ (v,u )}{∂(y,x)}\) ≠ 0
c) \(\frac {∂ (u,v)}{∂(x,y)}\) ≠ 0
d) ∂(u,v) + ∂(x,y) = 0
View Answer
Explanation: According to functional dependence concept in partial differentiation, when ‘u’ is a function of two variables (x, y) and ‘v’ is also a function of two variables (x, y), then the functional dependence between ‘u’ and ‘v’ is given by \(\frac {∂ ( u,v)}{∂(x,y)}\) = 0. If this condition satisfies, then the functions (u, v) are said to be functionally dependent on each other.
2. What is the meaning of functional dependence in partial differentiation when ‘u’ is a function of (x, y, z), ‘v’ is a function of (x, y, z) and ‘w’ is also a function of (x, y, z)?
a) J (u,v,w + x,y,z) = 0
b) \(\frac {∂ (u,v,w)}{∂(x,y,z)}\) = 0
c) \(\frac {∂ (u,v,w)}{∂(x,y,z)}\) ≠ 0
d) (u,v,w * x,y,z) = 0
View Answer
Explanation: According to functional dependence concept in partial differentiation, we have the Jacobian rule of J \(\frac {(u,v,w)}{(x,y,z)}\) = 0 (or) \(\frac {∂ (u,v,w)}{∂(x,y,z)}\) = 0. If this rule satisfies then the variables (u,v,w) are functionally dependent on each other, then we can find the relation among these three variables.
3. When two functions and two variables, say (u,v) and (x,y) are functionally dependent, then there will be no relation between (u,v) and (x,y).
a) True
b) False
View Answer
Explanation: According to functional dependence concept in partial differentiation, when two functions are functionally dependent, that is \(\frac {∂ ( u,v)}{∂(x,y)}\) = 0. Then there exist a relation between those 2 functions and also (u, v) are functionally dependent on (x, y).
4. What is the determinant of \(\frac {∂ (u,v)}{∂(x,y)}\) = 0, where ‘u’ is a function of (x, y) and ‘v’ is also the function of (x, y)?
a) \(\begin{vmatrix}
\frac {∂u}{∂x} & \frac {∂u}{∂y} \\
\frac {∂v}{∂x} & \frac {∂v}{∂y} \\ \end{vmatrix}\) = 0
b) \(\begin{vmatrix}
\frac {∂u}{∂x} & \frac {∂u}{∂y} \\
\frac {∂v}{∂x} & \frac {∂v}{∂y} \\ \end{vmatrix}\) ≠ 0
c) \(\begin{vmatrix}
\frac {∂v}{∂x} & \frac {∂v}{∂y} \\
\frac {∂u}{∂x} & \frac {∂u}{∂y} \\ \end{vmatrix}\) = 0
d) \(\begin{vmatrix}
\frac {∂v}{∂x} & \frac {∂v}{∂y} \\
\frac {∂u}{∂x} & \frac {∂u}{∂y} \\ \end{vmatrix}\) ≠ 0
View Answer
Explanation: In partial differentiation, functional dependence concept says that, when two functions are functionally dependent, then J\(\frac {(u,v,w)}{(x,y,z)}\) = 0 (or) \(\frac {∂ (u,v)}{∂(x,y)}\) = 0, to solve this jacobian we have to find the determinant of (u, v) in the form of partial derivatives, then there will be a relation between two functions, and also (u, v) are functionally dependent on (x, y).
5. Which among the following is a function of 2 variables?
a) Volume of a sphere(v) = \(\frac {4}{3}\)∏r3
b) Area of a rectangle (a) = length*breadth
c) Area of a square (a) = (side)2
d) Area of a circle (a) = ∏r2
View Answer
Explanation: Function of 2 variables means the function must consist of 2 variables. So, clearly area of the rectangle has 2 variables length and breadth, that is area of the rectangle has 2 variables, in volume of sphere and Area of circle we have only one variable which is radius. Similarly, for Area of square we have only one variable that is side.
6. Find the values of \(\frac {∂u}{∂x}\) and \(\frac {∂u}{∂y}\) where ‘u’ is a function of (x,y); u = \(\frac {x + y}{1-xy}\)?
a) \(\frac {∂u}{∂x} = \frac {1 + y}{1-xy}; \frac {∂u}{∂y} = \frac {1 + x}{1-xy}\)
b) \(\frac {∂u}{∂x} = \frac {1-y}{1 + xy}; \frac {∂u}{∂y} = \frac {1-x}{1 + xy}\)
c) \(\frac {∂u}{∂x} = \frac {(1 + y2}{(1-xy)^2}; \frac {∂u}{∂y} = \frac {1 + x2}{(1-xy)^{2}}\)
d) \(\frac {∂u}{∂x} = \frac {1 + y}{1 + xy}; \frac {∂u}{∂y} = \frac {1 + x}{1 + xy}\)
View Answer
Explanation: As the given variable ‘u’ is in the form of \(\frac {u}{v}\) differentiation rule which is \(\frac {u’v – v’u}{v^{2}}\) according to that \(\frac {∂u}{∂x} \frac {(1-xy)(1)-(x + y)(-y)}{(1-xy)^{2}}\)
\(\frac {∂u}{∂x} = \frac {(1-xy) + (x + y)(y)}{(1-xy)^{2}}\)
\(\frac {∂u}{∂x} = \frac {1-xy + xy + y2}{(1-xy)^{2}}\)
\(\frac {∂u}{∂x} = \frac {1 + y2}{(1-xy)^{2}}\)
\(\frac {∂u}{∂y} = \frac {(1-xy)-(x + y)(-x)}{(1-xy)^{2}}\)
\(\frac {∂u}{∂y} = \frac {(1-xy) + (x + y)(x)}{(1-xy)^{2}}\)
\(\frac {∂u}{∂y} = \frac {1-xy + xy + x2}{(1-xy)^{2}}\)
\(\frac {∂u}{∂y} = \frac {1 + x2}{(1-xy)^{2}}\)
7. Check whether the following functions (u, v) satisfy functional dependence or not.
Where u = y + z; v = x + 2z2; w = x – 4yz – 2y2
a) True
b) False
View Answer
Explanation: According to Functional dependence concept in partial differentiation, to know the functional dependence between 3 variables we should check \(\frac {∂ (u,v,w)}{∂(x,y,z)}\) = 0
\(\frac {∂ ( u,v,w)}{∂(x,y,z)} = \begin{vmatrix}
\frac {∂u}{∂x} & \frac {∂u}{∂y} & \frac {∂u}{∂z} \\
\frac {∂v}{∂x} & \frac {∂v}{∂y} & \frac {∂v}{∂z} \\
\frac {∂w}{∂x} & \frac {∂w}{∂y} & \frac {∂w}{∂z} \end{vmatrix}\)
\(\frac {∂u}{∂x}\) = 0; \(\frac {∂u}{∂y}\) = 1; \(\frac {∂u}{∂z}\) = 1; \(\frac {∂v}{∂x}\) = 1; \(\frac {∂v}{∂y}\) = 0; \(\frac {∂v}{∂z}\) = 4; \(\frac {∂w}{∂x}\) = 1; \(\frac {∂w}{∂y}\) = (-4y – 4y); \(\frac {∂w}{∂z}\) = -4y
\(\frac {∂ ( u,v,w)}{∂(x,y,z)} = \begin{vmatrix}
0 & 1 & 1 \\
1 & 0 & 4 \\
1 & (-4y-4y) & -4y \end{vmatrix}\)
= 0 – (-4y – 4y) + (-4y – 4y)
= 4y + 4y – 4y – 4y = 0
As \(\frac {∂ ( u,v,w)}{∂(x,y,z)}\) = 0 we can say that (u,v,w) are functionally dependent on (x,y,z).
Therefore, the given statement is true.
8. If partial derivatives \(\frac {∂f}{∂x}\) and \(\frac {∂f}{∂y}\) are intercepted on a graph, then what is the direction of tangent lines?
a) Gradients of the tangent lines to the surface z = f(x, y) in the directions parallel to the x-axis and y-axis
b) Angle between the tangent lines to the surface z = f(x, y) in the directions parallel to the x-axis and y-axis
c) Gradient of the tangent line to the surface z = f(x, y) in x-axis direction and angle between the tangent line to surface z = f(x, y) in the y-axis direction
d) Angle between the tangent line to the surface z = f(x, y) in x-axis direction and gradient of the tangent plane to surface z = f(x, y) in the y-axis direction
View Answer
Explanation: Gradient nature of tangent lines can be explained precisely using graphical explanation.
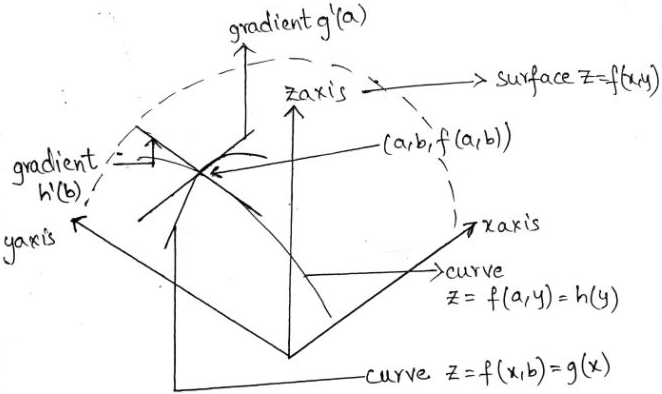
In the above figure we can see that, the complete interception is taken w.r.t z-axis or z surface. The curve z = f(x, b) is represented as g(x) and curve z = f(a, y) is represented as h(y). Now, with the help of these curves we can draw a gradient of the tangent g’ (a) parallel to x-axis and gradient of the tangent h’(b) is parallel to y-axis.
9. Check whether the following variables (u,v) are functionally dependent and derive the values of
\(\frac {∂u}{∂x} , \frac {∂u}{∂y}\) and \(\frac {∂u}{∂z}\) where u = xy + yz + zx, v = x2 + y2 + z2 and w = x + y + z2?
a) Yes, they are functionally dependent and \(\frac {∂u}{∂x}\) = y + z; \(\frac {∂u}{∂y}\) = x + z; \(\frac {∂u}{∂z}\) = y + x + z
b) No, they are not functionally dependent and \(\frac {∂u}{∂x}\) = y + z; \(\frac {∂u}{∂y}\) = x + z; \(\frac {∂u}{∂z}\) = y + x + z
c) Yes, they are functionally dependent and \(\frac {∂u}{∂x}\) = x + z; \(\frac {∂u}{∂y}\) = y + z; \(\frac {∂u}{∂z}\) = y + x + z
d) No, they are not functionally dependent and \(\frac {∂u}{∂x}\) = y + z; \(\frac {∂u}{∂y}\) = x + z; \(\frac {∂u}{∂z}\) = x + z
View Answer
Explanation: The given variables (u,v,w) are not functionally dependent with (x,y,z) because \(\frac {∂ ( u,v,w )}{∂(x,y,z)}\) ≠ 0.
\(\frac {∂(u,v,w)}{∂(x,y,z)} = \frac {∂u}{∂x}\) = y + z; \(\frac {∂u}{∂y}\) = x + z; \(\frac {∂u}{∂z}\) = x + y
= \(\frac {∂v}{∂x}\) = 2x; \(\frac {∂v}{∂y}\) = 2y; \(\frac {∂v}{∂z}\) = 2z
= \(\frac {∂w}{∂x}\) = 1; \(\frac {∂w}{∂y}\) = 1; \(\frac {∂w}{∂z}\) = 2z
\(\frac {∂ ( u,v,w)}{∂(x,y,z)} = \begin{vmatrix}
\frac {∂u}{∂x} & \frac {∂u}{∂y} & \frac {∂u}{∂z} \\
\frac {∂v}{∂x} & \frac {∂v}{∂y} & \frac {∂v}{∂z} \\
\frac {∂w}{∂x} & \frac {∂w}{∂y} & \frac {∂w}{∂z} \end{vmatrix} \)
\(\frac {∂ ( u,v,w)}{∂(x,y,z)} = \begin{vmatrix}
y + z & x + z & x + y \\
2x & 2y & 2z \\
1 & 1 & 2z \end{vmatrix} \)
\(\frac {∂ ( u,v,w)}{∂(x,y,z)}\) = 2\(\begin{vmatrix}
y + z & x + z & x + y \\
x & y & z \\
1 & 1 & 2z \end{vmatrix} \)
R1 → R1 + R2
From matrices, rows interchange concept, we can interchange row 1 with addition of row 1 + row 2.
\(\frac {∂ ( u,v,w)}{∂(x,y,z)}\) = 2\(\begin{vmatrix}
y + z & x + z & x + y \\
x & y & z \\
1 & 1 & 2z \end{vmatrix} \)
= 2[(x + y + z) (2yz – z) – (x + y + z)(2xz – z) + (x + y + z) (x – y)]
We can clearly see that \(\frac {∂ ( u,v,w)}{∂(x,y,z)}\) ≠ 0, therefore they are not functionally dependent.
10. How can we define the partial derivative \(\frac {∂f}{∂x}\) w.r.t to axis, where f is a function of 3 variables (x, y, z) and (a, b, c) are the points on the surface of the graph?
a) \(\frac {∂f}{∂x}\) = limit (h→0) \(\frac {f(h + a,b,c)-f(a,b,c)}{h} \)
b) \(\frac {∂f}{∂x}\) = limit (h→∞) \(\frac {f(a + h,b,c)-f(a,b,c)}{h} \)
c) \(\frac {∂f}{∂x}\) = limit (h→0) \(\frac {f(a + h,b,c)-f(a,b,c)}{h} \)
d) \(\frac {∂f}{∂x}\) = limit(h→∞) \(\frac {f(a + h,b,c)-f(a,b,c)}{h} \)
View Answer
Explanation: The partial derivative (\(\frac {∂f}{∂x}\)), can be expressed as the limit function or limit analogy, which is the extraction from ordinal derivatives. Here we are partially differentiate the function with respect to x, that is (\(\frac {∂f}{∂x}\)) and due to this condition, the ordinates ‘y’ and ‘z’ do not have any role in changing the gradients.
Sanfoundry Global Education & Learning Series – Engineering Mathematics.
To practice all areas of Engineering Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for 1st Year Engineering Internship
- Practice Probability and Statistics MCQ
- Check Engineering Mathematics Books
- Practice Numerical Methods MCQ
