This set of Differential and Integral Calculus Questions and Answers for Experienced people focuses on “Change of Variables In a Double Integral”.
1. Evaluation of \(\int\int_R f(x,y) \,dx \,dy \) in cartesian coordinate can be done using change of variables principle, among the choices given below which is correct explanation of change of variables principle? (Given let x=g(u,v) & y=h(u,v))
a) \(\int\int_S f(g(u,v),h(u,v)) \,du \,dv\)
b) \(\int\int_S f(g(u,v),h(u,v)) \frac{d(x,y)}{d(u,v)} \,du \,dv\)
c) \(\int\int_S f(g(u,v),h(u,v)) \frac{∂(x,y)}{∂(u,v)} \,du \,dv\)
d) \(\int\int_S f(g(u,v),h(u,v)) \frac{∂(u,v)}{∂(x,y)} \,du \,dv\)
View Answer
Explanation: \(\int\int_S f(g(u,v),h(u,v)) \frac{∂(x,y)}{∂(u,v)} \,du \,dv\)
where \( \frac{∂(x,y)}{∂(u,v)} = \begin{vmatrix}
\frac{∂x}{∂u} \frac{∂x}{∂v}\\
\frac{∂y}{∂u} \frac{∂y}{∂v}\\
\end{vmatrix} = J(\frac{x,y}{u,v}) = \frac{∂x}{∂u} \frac{∂y}{∂v} – \frac{∂x}{∂v} \frac{∂y}{∂u} …..\)(‘J’ is Jacobian).
2. The value of ∬R (x-y)2 dx dy where R is the parallelogram with vertices (0,0), (1,1),(2,0), (1,-1) when solved using change of variables is given by____
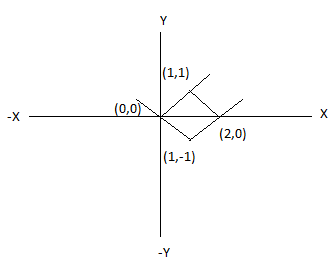
a) 16/3
b) 8/3
c) 4/3
d) 0
View Answer
Explanation: W.K.T from change of variables principle
\(\int\int_R f(x,y)\,dx \,dy = \int\int_S f(g(u,v),h(u,v)) \frac{∂(x,y)}{∂(u,v)} \,du \,dv …..(1)\)
From the above diagram in the region R the equations are given by
x-y=0, x-y=2, x+y=0, x+y=2 from this we can observe that change of
variables is u=x-y, v=x+y solving we get \(x=\frac{u+v}{2}, y=\frac{v-u}{2}\)
\(\frac{∂(x,y)}{∂(u,v)} = \begin{vmatrix}
\frac{∂x}{∂u}&\frac{∂x}{∂v}\\
\frac{∂y}{∂u}&\frac{∂y}{∂v}\\
\end{vmatrix} = \begin{vmatrix}
0.5 &0.5\\
-0.5&0.5\\
\end{vmatrix} = 0.5\)
The region S in the (u,v) is the square 0<u<2,0<v<2. Since x-y=u integral
becomes \(\int_0^2 \int_0^2 0.5u^2 \,du \,dv\)……from(1)
\(=\int_0^2 \Big[\frac{u^3}{6}\Big]_0^2 \,dv = \int_0^2 \frac{4}{3} dv = \frac{8}{3}.\)
3. If double integral in Cartesian coordinate is given by ∬R f(x,y) dx dy then the value of same integral in polar form is _____
a) ∬P f(r cos θ, rsin θ)dr dθ
b) ∬P f(r cosθ, r sinθ)rdr dθ
c) ∬P f(r cosθ, r sinθ) r2 dr dθ
d) ∬P f(r sinθ, r cosθ)dr dθ
View Answer
Explanation: ∬R f(x,y)dx dy when converting this into polar form we take x = r cos θ
y=r sin θ as change of variables from
\(\int\int_R f(x,y) \,dx \,dy = \int\int_S f(g(u,v),h(u,v)) \frac{∂(x,y)}{∂(u,v)} \,du \,dv \) where u=r & v=θ
thus \(\frac{∂(x,y)}{∂(r,θ)} =\begin{vmatrix}
\frac{∂x}{∂r} &\frac{∂x}{∂θ}\\
\frac{∂y}{∂r} &\frac{∂y}{∂θ}\\
\end{vmatrix} = \begin{vmatrix}
cosθ &-r sinθ\\
sinθ & rcosθ\\
\end{vmatrix} = r(cos^2 θ + sin^2 θ) = r\)
substituting we get ∬P f(r cos θ,r sin θ)rdr dθ.
4. The value of ∬R sin(x2 + y2) dx dy where R is the region bounded by circle centered at origin with radius r=2 is _____
a) πcos 4
b) π(1-cos 4)
c) π
d) π(1-sin 4)
View Answer
Explanation: Using Polar variable transformation x = r cos θ & y=r sin θ, r varies from 0 to 2 & θ varies from 0 to 2π because radius of circle i.e r=2 & centered at origin
\(\int\int_P f(r cos θ,r sin θ )rdr \,dθ = \int\int_R sin (x^2+y^2) \,dx \,dy = \int_0^2π \int_0^2 r sin r^2 \,dr \,dθ\)
Using substitution t=r2 integral changes to \(\int_0^{2π} \int_0^4 0.5 \,sint \,dt \,dθ\)
\(\int_0^{2π} 0.5\big[-cost\big]_0^4 dθ = \int_0^{2π} 0.5(1-cos4) dθ = π(1-cos 4)\).
5. Using change of variables principle in double integral we can reduce cartesian integral to simpler form.
a) True
b) False
View Answer
Explanation: The above statement is not necessarily true always but change of variables cartesian to polar form & changing into suitable form reduces the complexity in the evaluation of double integral however converse is also true for example ∬R x2 y3 dx dy is the given integral while solving there is no need of converting it into polar form since ∬P r6 cos2 θ sin3 θ dr dθ is tedious to solve when R only consists of constants but ∬R x2 y3 dx dy can be solved easily by ordinary method of integration.
Sanfoundry Global Education & Learning Series – Differential and Integral Calculus.
To practice all areas of Differential and Integral Calculus for Experienced people, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Numerical Methods MCQ
- Apply for 1st Year Engineering Internship
- Check Engineering Mathematics Books
- Practice Probability and Statistics MCQ
