This set of Complex Analysis Multiple Choice Questions & Answers (MCQs) focuses on “Functions of a Complex Variable”.
1. Find the domain of the function defined by f(z)=z/(z+z̅).
a) Im(z)≠0
b) Re(z)≠0
c) Im(z)=0
d) Re(z)=0
View Answer
Explanation: Write z=x+iy ⇒ f(x+iy)=(x+iy)/(x+iy+x-iy)=(x+iy)/2x
=1/2+iy/2x ⇒ x≠0 ⇒ Re(z)≠0 .
2. Let f(z)=z+1/z. What will be the definition of this function in polar form?
a) (r+1/r)cosθ+i(r-1/r)sinθ
b) (r-1/r)cosθ+i(r+1/r)sinθ
c) (r+1/r)sinθ+i(r-1/r)cosθ
d) (r+1/r)sinθ+i(r-1/r)cosθ
View Answer
Explanation: Write z=r(cosθ+isinθ), therefore, f(z)=z+1/z=r(cosθ+isinθ)+1/[r(cosθ+isinθ)]
=reiθ+(1/r)e-iθ=r(cosθ+isinθ)+1/r(cosθ-isinθ)=(r+1/r)cosθ+i(r-1/r)sinθ.
3. For the function f(z)=zi, what is the value of |f(ω)|+Arg f(ω), ω being the cube root of unity with Im(ω)>0?
a) e-2π/3
b) e2π/3
c) e-2π/3+2π/3
d) e-2π/3-2π/3
View Answer
Explanation: Let y=zi⇒ ln y=iln z=i(ln |z|+iarg z)=iln |z|-arg z
⇒ y=eiln |z|/earg z ⇒ |y|=earg z and Arg y=ln |z| ⇒ |f(ω)|+Arg f(ω)=e-2π/3+0=e-2π/3.
4. Let f(z)=(z2–z–1)7. If α2+α+1=0 and Im(α)>0, then find f(α).
a) 128α
b) -128α
c) 128α2
d) -128α2
View Answer
Explanation: Note that α=ω. Therefore, f(α)=f(ω)=(ω2–ω–1)7
=(ω2+ω2)7=(2ω2)7=27ω14=128ω2=128α2.
5. For all complex numbers z satisfying Im(z)≠0, if f(z)=z2+z+1 is a real valued function, then find its range.
a) (-∞, -1]
b) (-∞, 1/3)
c) (-∞, 1/2]
d) (-∞, 3/4)
View Answer
Explanation: Let y=f(z). then z2+z+1=y has imaginary roots (∵Im(z)≠0)
⇒ D<0 ⇒ 1–4(1–y)<0 ⇒ 4y<3 ⇒ y<3/4 . Also, putting Re z=-1/2 and Im z=∞, we get, f(z)=-∞.
6. Let x, y, z be integers, not all simultaneously equal. If ω is a cube root of unity with Im(ω)≠1, and if f(z)=az2+bz+c, then find the range of |f(ω)|.
a) (0, ∞)
b) [1, ∞)
c) (√3/2, ∞)
d) [1/2, ∞)
View Answer
Explanation: ω=-1/2+i√3/2. Therefore, |f(ω)|=|a+b(-1/2+i√3/2)+c(-1/2-i√3/2)|
=|(2a-b-c)/2+i(b√3-c√3)/2|=1/2[(2a-b-c)2+3(b-c)2]1/2={1/2[(a-b)2+(b-c)2+(c-a)2]}1/2. Putting b=c=0 and a=1 gives us the minimum value=1, while, a=∞ gives us the maximum value=∞.
7. Let f(z)=arg 1/(1 – z), then find the range of f(z) for |z|=1, z≠1.
a) (-∞, π/2)
b) (-π/2, π/2)
c) (-∞, ∞)
d) [0, π/2)
View Answer
Explanation: Let y=1/(1-z) ⇒ z=1-1/y
|z|=1 ⇒ |1-1/y|=1 ⇒ |y-1|=|y| ⇒ locus of y is the perpendicular bisector of line segment joining 0 and 1 ⇒ arg y ∈(-π/2, π/2).
8. Define f(z)=z2+bz−1=0 and g(z)=z2+z+b=0. If there exists α satisfying f(α)=g(α)=0, which of the following cannot be a value of b?
a) √3i
b) -√3i
c) 0
d) √3i/2
View Answer
Explanation: α2+bα−1=0 and α2+α+b=0 ⇒ (b−1)α−1−b=0 ⇒ α=(b+1)/(b-1)
⇒ (b+1)2/(b-1)2+(b+1)/(b-1)+b=0 ⇒ b=√3i, -√3i, 0.
9. Let f(z)=2(z+z̅)+3i(z-z̅) and g(z)=|z|. f(z)=2 divides the region g(z)≤6 into two parts. If Q={(2+3i/4), (5/2+3i/4), (1/4-i/4), (1/8+i/4)}, then find the number of elements of Q lying inside the smaller part.
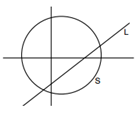
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: Writing z=x+iy, we get L as 2x–3y–1 and S as x2+y2–6, a point z1 lies in the smaller region if L1>0 and S1<0. ∴ (2+3i/4) and (1/4-i/4) lie in the smaller region.
10. Find the range of the function defined by f(z)=Re[2iz/(1-z2)].
a) (−∞, 0) ⋃ (0, ∞)
b) [2, ∞)
c) (−∞, −1] ⋃ [1, ∞)
d) (−∞, 0] ⋃ [2, ∞)
View Answer
Explanation: z=2i(x+iy)/(1-(x+iy)2)=2i(x+iy)/(1-(x2-y2+2ixy))
Using 1-x2=y2, z=(2ix-2y)/(2y2-2ixy)=-1/y
∵ –1≤y≤1 ⇒ –1/y≤-1 or -1/y≥1.
11. Let f(z)=|z|2+Re z(2(z+z̅)+3(z-z̅)/2i, the find the maximum value of |z|2/f(z).
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: Write z=|z|(cosθ+isinθ) ⇒ |z|2/f(z)=1/(1+4cos2θ+3sinθcosθ)
=1/(1+4cos2θ+3/2sin2θ)=1/[2(1+cos2θ)+1+3/2sin2θ].
Now, 2(1+cos2θ)+1+3/2sin2θ=3+2cos2θ+3/2sin2θ≥3-(4+9/4)1/2=1/2.
Hence, maximum value is 2.
12. Consider a function f(z) of degree two, having real coefficients. If z1 and z2 satisfying f(z1)=f(z2)=0 are such that Re z1=Re z2=0 and if z3 satisfies f(f(z3))=0, then select the correct statement.
a) Re z3=0
b) Im z3=0
c) Re z3×Imz3≠0
d) Re z3=0 and Im z3=0
View Answer
Explanation: f(z)=az2+b, with a, b of same sign ⇒ f(f(z))=a(az2+b)2+b
If z∈R or iz∈R ⇒ z2∈R ⇒ f(z)∈R ⇒ f(f(z))≠0 ⇒ Hence real or purely imaginary number cannot satisfy f(f(z))=0.
13. Let f(z)=|1–z|, if zk=cos(2kπ/10)+isin(2kπ/10), then find the value of f(z1)×f(z2)×…×f(z9).
a) 10
b) 15
c) 20
d) 30
View Answer
Explanation: z10–1=(z-1)(z-z1)…(z-z9) ⇒ (z-z1)(z-z2) …(z-z9)=1+z+z2+…+z9.
Now, putting z=1, we get, (z-z1)(z-z2)…(z-z9)=f(z1)×f(z2)×…×f(z9)=10.
14. For a∈R, let f(z)=z5-5z+a. Select the correct statement for α satisfying f(α)=0.
a) α has exactly three possible real values for a>4
b) α has exactly one possible real value for a>4
c) α has exactly three possible real values for a<-4
d) α has exactly one possible real value for -4<a<4
View Answer
Explanation: z5-5z+a=0 ⇒ z5-5z=-a ⇒ z(z-51/4)(z+51/4)(z2+51/2)=-a f'(z)=5z4–5=0 ⇒ (z2+1)(z2-1)=0 ⇒ (z-1)(z+1)(z2+1)=0 ⇒ α has exactly one possible real value for a>4 and exactly three possible real values for -4<a<4.
15. Let f(z)=z4+a1z3+a2z2+a3z+a4=0; a1, a2, a3, a4 being real and non-zero. If f has a purely imaginary root, then what is the value of the expression a3/(a1a2)+ a1a4/(a2a3) ?
a) 0
b) 1
c) -2
d) 2
View Answer
Explanation: For real x(≠0), let ix be the root⇒x4-a1x3i- a2x2+a3xi+a4=0⇒x4-a2x2+a4=0 and a1x3-a3x=0
a1x3-a3x=0 ⇒ a1x2-a3=0 ⇒x2=a3/a1, putting this value in the equation, a3/(a1a2)+a1a4/(a2a3)=1.
Sanfoundry Global Education & Learning Series – Complex Analysis.
To practice all areas of Complex Analysis, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Engineering Mathematics Books
- Apply for 1st Year Engineering Internship
- Practice Numerical Methods MCQ
- Practice Probability and Statistics MCQ
