This set of Differential and Integral Calculus Multiple Choice Questions & Answers (MCQs) focuses on “Derivatives of Area”.
1. What is the maximum area of the rectangle with perimeter 620 mm?
a) 24,025 mm2
b) 22,725 mm2
c) 24,000 mm2
d) 24,075 mm2
View Answer
Explanation: Let x be the length of the rectangle and y be the width of the rectangle. Then, Area A is,
A=x*y …………………………………………………. (1)
Given: Perimeter of the rectangle is 620 mm. Therefore,
P=2(x+y)
620=2(x+y)
x+y=310
y=310-x
We can now substitute the value of y in (1)
A=x*(310-x)
A=310x-x2
To find maximum value we need derivative of A,
dA/dx=310-2x
To find maximum value, \(\frac{dA}{dx}=0 \)
310-2x=0
2x=310
x=155 mm
Therefore, when the value of x=155 mm and the value of y=310-155=155 mm, the area of the rectangle is maximum, i.e., A=155*155=24,025 mm2
2. Power Rule of the derivative states that, \(\frac{d(x^n)}{dx}=nx^{n-1}.\)
a) True
b) False
View Answer
Explanation: Power Rule is given by, \(\frac{d(x^n)}{dx}=nx^{n-1}.\)
For example, \(\frac{d(x^4)}{dx}=4x^3. \)
3. Which of the following trigonometric function derivatives is correct?
a) \(\frac{d(sinx)}{dx}=-cosx\)
b) \(\frac{d(secx)}{dx}=secxtanx\)
c) \(\frac{d(tanx)}{dx}=cot^2 x\)
d) \(\frac{d(cosx)}{dx}=sinx\)
View Answer
Explanation: Correct forms of Trigonometric Derivative Functions
- \(\frac{d(sinx)}{dx}=cosx \)
- \(\frac{d(cosx)}{dx}=-sinx\)
- \(\frac{d(secx)}{dx}=secxtanx\)
- \(\frac{d(tanx)}{dx}=sec^2 x \)
4. Product Rule of the derivative is given by ________
a) \(\frac{d(fg)}{dx}=\frac{d(g)}{dx}*\frac{d(f)}{dx}\)
b) \(\frac{df}{dx}*\frac{dg}{dx}=\frac{d(g)}{dx}+\frac{d(f)}{dx}\)
c) \(\frac{d(fg)}{dx}=f \frac{d(g)}{dx}*g \frac{d(f)}{dx}\)
d) \(\frac{d(fg)}{dx}=f \frac{d(g)}{dx}+g \frac{d(f)}{dx}\)
View Answer
Explanation: Product Rule of derivative is given by,
\( \frac{d(fg)}{dx}=f \frac{d(g)}{dx}+g \frac{d(f)}{dx}\)
5. What is the derivative of \(\frac{3x^2}{(1-sinx)}\)?
a) \(\frac{6xsinx-3x^2 cosx}{(1-sinx)^2} \)
b) \(\frac{6x}{1-sinx} \)
c) \(\frac{6xsinx-3x^2 cosx-6x}{(1-sinx)^2} \)
d) \(\frac{6xsinx-3cosx-6}{(1-sinx)^2} \)
View Answer
Explanation: Given: y = \(\frac{3x^2}{(1-sinx)}\)
\(\frac{dy}{dx}=\frac{3x^2(\frac{d(1-sinx)}{dx})-(\frac{d(3x^2)}{dx})(1-sinx)}{(1-sinx)^2}\)
\(\frac{dy}{dx}=\frac{3x^2(-cosx)-6x(1-sinx)}{(1-sinx)^2}\)
\(\frac{dy}{dx}=\frac{6xsinx-3x^2 cosx-6x}{(1-sinx)^2}\)
6. Which of the following is a type of Iterative method of solving non-linear equations?
a) Graphical method
b) Interpolation method
c) Trial and Error methods
d) Direct Analytical methods
View Answer
Explanation: There are 2 types of Iterative methods, (i) Interpolation methods (or Bracketing methods) and (ii) Extrapolation methods (or Open-end methods).
7. The half-interval method in numerical analysis is also known as __________
a) Newton-Raphson method
b) Regula Falsi method
c) Taylor’s method
d) Bisection method
View Answer
Explanation: The Bisection method, also known as binary chopping or half-interval method, is a starting method which is used, where applicable, for few iterations, to obtain a good initial value.
8. Given \(∫_0^8 x^{\frac{1}{3}} dx,\) find the error in approximating the integral using Simpson’s \(\frac{1}{3}\) Rule with n=4.
a) 1.8
b) 2.9
c) 0.3
d) 0.35
View Answer
Explanation: Given: \(∫_0^8 x^{\frac{1}{3}} dx,\), n = 3,
Let \(f(x)= x^{\frac{1}{3}},\)
\(∆x = \frac{b-a}{2}=\frac{8-0}{2}=4\)………………since b=8, a=0 (limits of the given integral)
Hence endpoints xi have coordinates {0, 2, 4, 6, 8}.
Calculating the function values at xi, we get,
\(f(0)= 0^{\frac{1}{3}}=0\)
\(f(2)= 2^{\frac{1}{3}}\)
\(f(4)= 4^{\frac{1}{3}}\)
\(f(6)= 6^{\frac{1}{3}}\)
\(f(8)= 8^{\frac{1}{3}} =2\)
Substituting these values in the formula,
\(∫_0^8x^{\frac{1}{3}} dx ≈ \frac{∆x}{3} [f(0)+4f(2)+2f(4)+4f(6)+f(8)]\)
\(≈ \frac{2}{3}[0+4(2^{\frac{1}{3}})+ 2(4^{\frac{1}{3}})+ 4(6^{\frac{1}{3}})+2] ≈ 11.65\)
Actual integral value,
\(∫_0^8x^{\frac{1}{3}}dx = \left(\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right)_0^8=12\)
Error in approximating the integral = 12 – 11.65 = 0.35
9. A sphere with the dimensions is shown in the figure. What is the error that can be incorporated in the radius such that the volume will not change more than 8%?
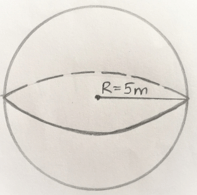
a) 0.127%
b) 0.02546%
c) 0.002546%
d) 0.2546%
View Answer
Explanation: We know that volume of the sphere is,
\(V = \frac{4}{3} πR^3 \)
Differentiating the above equation with respect to R we get,
\(\frac{dV}{dR} = \frac{4}{3} π×3R^2=4πR^2\)
Since the volume of the sphere should not exceed more than 8%,
\(dR=\frac{dV}{4πR^2}=\frac{0.08}{4π(5)^2}=0.0002546\)
Error in radius = 0.02546%
10. Half Range Fourier Series contains either sine or cosine terms.
a) True
b) False
View Answer
Explanation: A series which contains only sine or cosine terms is called Half Range Fourier Sine Series or Cosine Series respectively.
Sanfoundry Global Education & Learning Series – Differential and Integral Calculus.
To practice all areas of Differential and Integral Calculus, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for 1st Year Engineering Internship
- Practice Numerical Methods MCQ
- Check Engineering Mathematics Books
- Practice Probability and Statistics MCQ
