This set of Differential and Integral Calculus MCQs focuses on “Change of Variables In a Triple Integral”.
1. For the below-mentioned figure, conversion from cartesian coordinate ∭R f(x,y,z)dx dy dz to cylindrical polar with coordinates p(ρ,∅,z) is given by ______
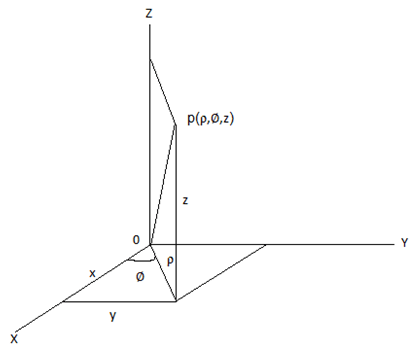
a) ∭R* f(ρ,∅,z) ρ dρ d∅ dz
b) ∭R f(ρ,∅,z) dρ d∅ dz
c) ∭R*f(ρ,∅,z) ρ∅ dρ d∅ dz
d) ∭R f(ρ,∅,z) ρ2 dρ d∅ dz
View Answer
Explanation: From the figure we can write x=ρ cos ∅, y=ρ sin ∅, z=z
now we know that during change of variables f(x,y,z) is replaced by
\(f(ρ,∅,z)*J\left(\frac{x,y,z}{ρ,∅,z}\right)\) with limits in functions of x,y,z to functions of ρ,∅,z respectively
\(J\left(\frac{x,y,z}{ρ,∅,z}\right)= \begin{vmatrix}
\frac{∂x}{∂p} & \frac{∂x}{∂∅} &\frac{∂x}{∂z}\\
\frac{∂y}{∂p} &\frac{∂y}{∂∅} &\frac{∂y}{∂z}\\
\frac{∂z}{∂p} &\frac{∂z}{∂∅} &\frac{∂z}{∂z}\\
\end{vmatrix}
= \begin{vmatrix}
cos∅ &-p sin∅ &0\\
sin∅ &p cos∅ &0\\
0 &0 &1\\
\end{vmatrix} = cos ∅(ρ cos ∅) + ρ sin ∅ (sin ∅)\)
= ρ, thus ∭R f(x,y,z)dx dy dz = ∭R* f(ρ,∅,z) ρ dρ d∅ dz where R* is the new region.
2. For the below mentione figure ,conversion from cartesian coordinate ∭R f(x,y,z)dx dy dz to spherical polar with coordinates p(r,θ,∅) is given by ______
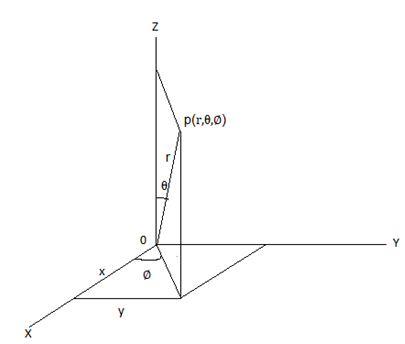
a) ∭R* f(r,θ,∅) sinθ dr dθ d∅
b) ∭R* f(r,θ,∅) r2 dr dθ d∅
c) ∭R* f(r,θ,∅) r2 cosθ dr dθ d∅
d) ∭R* f(r,θ,∅) r2 sinθ dr dθ d∅
View Answer
Explanation: From the figure we can write x = r sin θ cos ∅, y = r sin θ sin ∅, z = r cos θ
now we know that during a change of variables f(x,y,z) is replaced by \(f(ρ,∅,z)*J\left(\frac{x,y,z}{ρ,∅,z}\right)\) with limits in functions of x,y,z to functions of r,θ,∅ respectively
\(J\left(\frac{x,y,z}{ρ,∅,z}\right) =\begin{vmatrix}
\frac{∂x}{∂r} &\frac{∂x}{∂θ} &\frac{∂x}{∂∅}\\
\frac{∂y}{∂r} &\frac{∂y}{∂θ}& \frac{∂y}{∂∅}\\
\frac{∂z}{∂r} &\frac{∂z}{∂θ} &\frac{∂z}{∂∅}\\
\end{vmatrix} = \begin{vmatrix}
sin θ cos ∅ &r cos θ cos ∅ &-r sin θ sin ∅\\
sin θ sin ∅ &r cos θ sin ∅ &r sin θ cos ∅\\
cos θ& -r sin θ &0\\
\end{vmatrix}\)
= sin θ cos ∅(r2 sin2 θ cos∅) + r cos θ cos ∅(r sin θ cos ∅ cos θ) – r sin θ sin ∅
= (-r sin2 θ sin∅-r cos2 θ sin∅)……on solving we get r2 sinθ
thus ∭R f(x,y,z)dx dy dz = ∭R* f(r,θ,∅)r2 sinθ dr dθ d∅ where R* is the new region.
3. If ∭R xyz dx dy dz is solved using cylindrical coordinate where R is the region bounded by the planes x=0, y=0, z=0, z=1 & x2+y2=1 then what is the value of that integral?
a) 1/24
b) 1/16
c) 1/4
d) 1/2
View Answer
Explanation: x2+y2=1→ρ varies from 0 to 1 substituting x=ρ cos ∅, y=ρ sin ∅, z=z
z varies from 0 to1, x=0, y=0→∅ varies from 0 to π/2
thus the given integral is changed to cylindrical polar given by
\(\int_0^{\frac{π}{2}} \int_ 0^1 \int_0^1 cos∅sin∅ ρ^3 z \,dz \,dρ \,d∅ = \int_0^{\frac{π}{2}} \int_ 0^1 cos∅sin∅ ρ^3 \Big[\frac{z^2}{2}\Big]_0^1 \,dρ \,d∅\)
\(\int_0^{\frac{π}{2}} cos∅sin∅ \Big[\frac{ρ^3}{8}\Big]_0^1 \,d∅ = \int_0^{\frac{π}{2}} cos∅sin∅ \frac{1}{8} \,d∅ \)
put sin ∅=t, dt=cos ∅
t varies from 0 to 1 \(\int_ 0^1 \frac{1}{8} t \,dt = \Big[\frac{t^2}{16}\Big]_0^1 = \frac{1}{16}.\)
4. The volume of the region R defined by inequalities 0≤z≤1, 0≤y+z≤2,0≤x+y+z≤3 is given by ______
a) 4
b) 6
c) 8
d) 1
View Answer
Explanation: It is observed from equations that the region is made of parallelepiped thus volume of parallelepiped is given by triple integral over the given region.
i.e by using substitutions as x+y+z=p, y+z=q, z=r the new region becomes R* where p varies from 0 to 3, q varies from 0 to 2 & r varies from 0 to 1 jacobian of this transformation is given by
\(J\left(\frac{p,q,r}{x,y,z}\right) = \begin{vmatrix}
\frac{∂p}{∂x} & \frac{∂p}{∂y} &\frac{∂p}{∂z}\\
\frac{∂q}{∂x} &\frac{∂q}{∂y} &\frac{∂q}{∂z}\\
\frac{∂r}{∂x} &\frac{∂r}{∂y} &\frac{∂r}{∂z}\\
\end{vmatrix} = \begin{vmatrix}
1&1&1\\
0&1&1\\
0&0&1\\
\end{vmatrix} = 1(1) – 1(0) + 1(0) = 1\)
but we need \(J\left(\frac{x,y,z}{p,q,r}\right) \,w.k.t\, J\left(\frac{x,y,z}{p,q,r}\right) J\left(\frac{p,q,r}{x,y,z}\right) = 1 \,thus\, J\left(\frac{x,y,z}{p,q,r}\right)=1\)
now the volume is given by \(\int_ 0^1 \int_ 0^2\int_ 0^3 \,dp \,dq \,dr = \int_ 0^1 \int_ 0^2 3\, dq \,dr = \int_ 0^1 6dr = 6.\)
5. What is the value of integral \(∭_Re^{{(x^2+y^2+z^2)}^{\frac{3}{2}}} \,dx \,dy \,dz \) where R is the region given by x2+y2+z2≤1?
a) \(\frac{4π(e-1)}{3}\)
b) \(\frac{4π(e^3-1)}{3}\)
c) \(\frac{4π(e^2+1)}{3}\)
d) \(\frac{8π(e+1)}{3}\)
View Answer
Explanation: It can be noticed that R is the region bounded by sphere from the equation x2+y2+z2≤1 thus we are using spherical coordinate to solve this problem
i.e clearly radius r varies from 0 to 1, θ varies from 0 to π & ∅ varies from 0 to 2π
thus the given integral changes to \(\displaystyle∭_{R^*} e^{{r}^{{2}^{1.5}}}\) r2 sinθ dr dθ d∅
\(e^{{r}^{{2}^{1.5}}}\) is obtained by substituting x = r sin θ cos ∅, y = r sin θ sin ∅, z=r cos θ & hence solving the same, now substituting R* we get
\(\displaystyle\int_ 0^{2π} \int_ 0^π \int_ 0^1 e^{{r}^{{2}^{1.5}}} r^2 \, sinθ \,dr \,dθ \,d∅ = \int_ 0^{2π} d∅ \int_ 0^π sinθ \,dθ \int_ 0^1 r^2 e^{{r}^{3}} \,dr\)
\(2π*\Big[-cosθ\Big]_0^π * \frac{1}{3} \Big[e^{{r}^{3}}\Big]_{r^3=0}^{r^3=1}=\frac{4π(e-1)}{3}.\)
Sanfoundry Global Education & Learning Series – Differential and Integral Calculus.
To practice MCQs on all areas of Differential and Integral Calculus, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Engineering Mathematics Books
- Apply for 1st Year Engineering Internship
- Practice Probability and Statistics MCQ
- Practice Numerical Methods MCQ
