Differential Calculus Multiple Choice Questions

This set of Differential Calculus Multiple Choice Questions & Answers focuses on “Polar Curves”.

1. For the below mentioned figure the angle between radius vector (op) ⃗ and tangent to the polar curve where r=f(θ) has the one among the following relation?

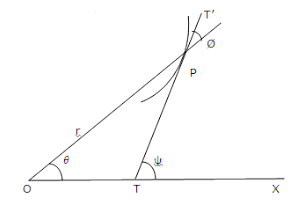
a) \(tan\,⁡ω=\frac{tan⁡∅+tan⁡θ}{1-tan⁡∅tan⁡θ}\)
b) \(tan⁡\,ω=\frac{tan⁡∅-tan⁡θ}{1+tan⁡∅tan⁡θ}\)
c) \(tan\,⁡∅=r(\frac{dr}{dθ})\)
d) \(tan⁡\,ω=tan⁡∅+tan⁡θ \)
View Answer

Answer: a
Explanation: From the fig (1) ω=∅+θ…….. (triangle rule & \(\hat{opt}\) = ∅)
tan ⁡ω=tan(⁡θ+∅)
\(tan⁡\,ω=\frac{tan⁡∅+tan⁡θ}{1-tan⁡∅tan⁡θ}\) ……(1) further more w.k.t x=rcos⁡θ, y=rsin⁡θ
But \(tan\,⁡ω = \frac{dy}{dx}\)……(slope of the tangent TT’)
\(tan\,ω = \frac{\frac{dy}{dθ}} {\frac{dx}{dθ}}\)……..since x & y are functions of θ
i.e \(\displaystyle tan⁡\,ω = \frac{\frac{d(r sin⁡θ)}{dθ}}{\frac{d(r cos⁡θ)}{dθ}} = \frac{r cos⁡θ + \frac{dr}{dθ} sin⁡θ}{-r sin⁡θ + \frac{dr}{dθ} cos⁡θ}\)
\(\displaystyle tan⁡\,ω = \frac{\frac{r cos⁡θ} {\frac{dr}{dθ} cos⁡θ} + \frac{\frac{dr}{dθ} sin⁡θ}{\frac{dr}{dθ} cos⁡θ}} {\frac{-r sin⁡θ}{\frac{dr}{dθ} cos⁡θ}+\frac{\frac{dr}{dθ} cos⁡θ}{\frac{dr}{dθ} cos⁡θ}} = \frac{\frac{r}{\frac{dr}{dθ}}+tan⁡θ}{\frac{r}{\frac{dr}{dθ}}tan⁡θ}\)…………(2)
from (1) &(2)
\(tan⁡∅ = \frac{r}{\frac{dr}{dθ}} = r (\frac{dθ}{dr}).\)

2. The angle between Radius vector r=a(1-cos⁡θ)and tangent to the curve is ∅ given by _______
a) ∅=\(\frac{π}{2}\)
b) ∅=π
c) ∅=\(-\frac{π}{2}\)
d) ∅=0
View Answer

Answer: a
Explanation: r= a(1-cos⁡θ)
taking logarithms on both sides we get,
log⁡r = log⁡a + log⁡(1-cos⁡θ)
differentiating w.r.t θ we get,
\( \frac{1}{r} \frac{dr}{dθ} = 0 + \frac{sin⁡θ}{1-cos⁡θ}\)
\(\frac{1}{r} \frac{dr}{dθ} = \frac{2 sin ⁡\frac{θ}{2} cos⁡\frac{θ}{2}}{2sin^2 \frac{θ}{2}} = cot⁡\frac{θ}{2}\) ..(1),
but \(cot⁡∅ = \frac{1}{r} \frac{dr}{dθ}\)….(2)
From (1)&(2)
∅=\(\frac{π}{2}\).

3. Angle of intersection of two polar curves is equal to the angle between the tangents drawn at the point of intersection of the two curves then What is the condition for the two curves intersecting orthogonally for the below mentioned figure?

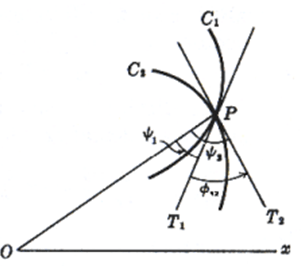
a) tan φ1⁡ . tan⁡φ3=1
b) tan⁡φ1 . tan⁡φ3=-1
c) tan⁡(φ1+φ3)=\(\frac{1}{\sqrt{2}}\)
d) tan⁡(φ1-φ3)=\(\frac{1}{\sqrt{2}}\)
View Answer

Answer: b
Explanation: From the figure & according to orthogonal principle |φ1-φ3|=\(\frac{π}{2}\)
further φ1=\(\frac{π}{2}\)+φ3……taking tangent of the angle
\(tan⁡ φ1 = tan(⁡\frac{π}{2}+φ3) = -cot⁡φ3 = -\frac{1}{tan⁡φ3} \)
tan⁡φ1 .tan⁡φ3 = -1.

4. Angle of intersection between two polar curves given by r=a(1+sin⁡θ) & r=a(1-sin⁡θ) is given by ________
a) \(\frac{π}{4}\)
b) \(\frac{π}{2}\)
c) Π
d) 0
View Answer

Answer: b
Explanation: r=a(1+sin⁡θ) : r=a(1-sin⁡θ)
taking logarithm on both the equations
log⁡r = log⁡a + log⁡(1+sin⁡θ) : log⁡r = log⁡a + log⁡(1-sin⁡θ)
differentiating on both side we get
\( \frac{1}{r} \frac{dr}{dθ} = \frac{cos⁡θ}{1+sin⁡θ} : \frac{1}{r} \frac{dr}{dθ} = \frac{-cos⁡θ}{1-sin⁡θ}\)
\(cot⁡∅1 = \frac{cos⁡θ}{1+sin⁡θ} : cot⁡∅2 = \frac{-cos⁡θ}{1-sin⁡θ}\)
where ∅1&∅2 are the angle between tangent & the vector respectively
\(tan⁡∅1 = \frac{1+sin⁡θ}{cos⁡θ} : tan⁡∅2 = \frac{1-sin⁡θ}{cos⁡θ}\)
\(tan⁡∅1 . tan⁡∅2 = \frac{1+sin⁡θ}{cos⁡θ} . \frac{1-sin⁡θ}{-cos⁡θ} = \frac{1-sin^2 θ}{-cos^2 θ} = -\frac{cos^2 θ}{cos^2 θ} = -1\)
above is the condition of orthogonality of two polar curves thus
|∅1-∅2|=\(\frac{π}{2}\).

5. One among the following is the correct explanation of pedal equation of an polar curve, r=f (θ), p=r sin(∅) (where p is the length of the perpendicular from the pole to the tangent & ∅ is the angle made by tangent to the curve with vector drawn to curve from pole)is _______
a) It is expressed in terms of p & θ only
b) It is expressed in terms of p & ∅ only
c) It is expressed in terms of r & θ only
d) It is expressed in terms of p& r only
View Answer

Answer: d
Explanation: It is expressed in terms of p& r only
where p=r sin(∅) & \(tan⁡∅ = \frac{r}{\frac{dr}{dθ}} = r (\frac{dr}{dθ})\)
& r=f (θ) or after solving we get direct relationship between p & r as
\(\frac{1}{p^2} = \frac{1}{r^2} cosec^2∅.\)

Subscribe Now: Engineering Mathematics Newsletter | Important Subjects Newsletters

6. The pedal Equation of the polar curve rⁿ=aⁿ cos⁡nθ is given by ______
a) rⁿ=paⁿ
b) r^n-1=paⁿ
c) rⁿ⁺¹=paⁿ⁺¹
d) rⁿ⁺¹=paⁿ
View Answer

Answer: d
Explanation: Taking logarithm for the given curve we get
n log⁡r = n log⁡a + log⁡(cos⁡nθ)
differentiating w.r.t θ, we get
\(\frac{n}{r} \frac{dr}{dθ} = \frac{-n sin⁡nθ}{cos⁡nθ} \rightarrow \frac{1}{r} \frac{dr}{dθ} = -tan⁡θ\)
thus \(cot⁡∅ = cot⁡(\frac{π}{2} + nθ)\rightarrow ∅ = \frac{π}{2} + nθ……(1)\)
from the eqn w.k.t p=r sin ∅
substituting from (1)
p = r sin (\(\frac{π}{2}\) + nθ) = r cos (nθ), but we have rⁿ = aⁿ cos⁡nθ
hence dividing them we get \(\frac{p}{r^n} = \frac{r cos (nθ)}{a^n cos⁡nθ}\)
rⁿ⁺¹=paⁿ.

7. The length of the perpendicular from the pole to the tangent at the point θ=\(\frac{π}{2}\) on the curve. r=a sec²(\(\frac{π}{2}\)) is _____
a) \(p = \frac{2a}{\sqrt{3}}\)
b) \(p = \frac{4a}{\sqrt{3}}\)
c) \(p = 2a\sqrt{2}\)
d) p = 4a
View Answer

Answer: c
Explanation: Taking Logarithm on both side of the polar curve
we get log⁡r = log⁡a + 2 log⁡sec⁡(\(\frac{θ}{2}\))
differentiating w.r.t θ we get
\(\frac{1}{r} \frac{dr}{dθ} = \frac{2 sec⁡(\frac{θ}{2}).tan⁡(\frac{θ}{2}) }{2 sec⁡(\frac{θ}{2})} = tan⁡(\frac{θ}{2})\)
\(cot⁡∅ = cot⁡(\frac{π}{2} – \frac{θ}{2}) \rightarrow ∅ = \frac{π}{2} -\frac{θ}{2}\)
w.k.t length of the perpendicular is given by p=r sin ∅
thus substituting ∅ value we get \(p = r \,sin(\frac{π}{2} – \frac{θ}{2}) = r \,cos(\frac{θ}{2})\)
at \( θ=\frac{π}{4}, p = r \,cos \frac{π}{4} = \frac{r}{\sqrt{2}}….(1)\)
but \( r=a \,sec^2 (\frac{θ}{2}) \,at\, θ = \frac{π}{4}, r=a \,sec^2 (\frac{π}{4}) = 4a…(2)\)
from (1) & (2) \(p=\frac{4a}{\sqrt{2}} = 2a\sqrt{2}\).

8. Polar equations of the circle for the given coordinate (x,y) which satisfies the equation given by (x-a)²+(y-b)²=r² where (a,b) is the coordinates of the centre of the circle &r is the radius.
a) x = r cos⁡θ, y = r sin⁡θ
b) x = a+ r cos⁡θ, y = b + r sin⁡θ
c) y = a+r cos⁡θ, x = b + r sin⁡θ
d) x = r sin⁡θ, y = r cos⁡θ
View Answer

Answer: b
Explanation: option x = a+ r cos⁡θ, y = b + r sin⁡θ satisfies the equation (x-a)²+(y-b)²=r²
because LHS=(a+r cos⁡θ-a)² + (b+ r sin⁡θ-b)² = r²(cos² θ + sin² θ)= r²=RHS.

9. In an polar curve r=f (θ) what is the relation between θ & the coordinates (x,y)?
a) tan⁡θ = \(\frac{x}{y} \)
b) (1+sin⁡θ) = \(\frac{y}{x} \)
c) (1+sec² θ) = \(\frac{y^2}{x^2} \)
d) (1+cos⁡θ) = \(\frac{x}{y} \)
View Answer

Answer: c
Explanation: w.k.t for the polar curve r=f (θ) x=rcos⁡θ, y=rsin⁡θ
dividing them we get \(\frac{y}{x} = \frac{r sin⁡θ}{r cos⁡θ} = tan⁡θ\)
squaring on both side \(\frac{y^2}{x^2} = tan^2 θ = (1+sec^2 θ)\).

Sanfoundry Global Education & Learning Series – Differential Calculus.

To practice all areas of Differential Calculus, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Engineering Mathematics Questions and Answers – Indeterminate Forms – 4

» Next - Differential Calculus Questions and Answers – Derivative of Arc Length

Related Posts:

Check Engineering Mathematics Books
Practice Probability and Statistics MCQ
Apply for 1st Year Engineering Internship
Practice Numerical Methods MCQ

Recommended Articles: