This set of Complex Integration Multiple Choice Questions & Answers (MCQs) focuses on “Cauchy’s Integral Theorem”.
1. Which of the following is the statement of Cauchy’s Integral Theorem?
a) If a function f (z) is analytic and its derivative f’ (z) is continuous at all points inside and on a simple closed curve C, then ∫C f(z) dz = 0
b) If a function f (z) is non-analytic and its derivative f’ (z) is continuous at all points inside and on a simple closed curve C, then ∫C f(z) dz = 0
c) If a function f (z) is analytic and its derivative f’ (z) is discontinuous at all points inside and on a simple closed curve C, then ∫C f(z) dz = 0
d) If a function f (z) is non-analytic and its derivative f’ (z) is discontinuous at all points inside and on a simple closed curve C, then ∫C f(z) dz = 0
View Answer
Explanation: Cauchy’s Integral Theorem states that ‘If a function f (z) is analytic and its derivative f’ (z) is continuous at all points inside and on a simple closed curve C, then ∫C f(z) dz = 0
Let us consider f (z) = u (x, y) + i v (x, y)
We take a complex function z = x + iy; dz = dx + idy
\(∫_Cf(z)dz= ∫_C(u+iv)(dx+idy)= ∫_C(udx-vdy)+i∫_C(vdx+udy)\) ———— (1)
As f’(z) is continuous, the four partial derivatives \(\frac{∂u}{∂x},\frac{∂u}{∂y}, \frac{∂v}{∂x},\frac{∂v}{∂y} \)are also continuous in R and C.
From (1)
\(∫_Cf(z)dz= ∬_R(\frac{-∂v}{∂x}-\frac{-∂u}{∂y})dx dy + i ∬_R(\frac{∂u}{∂x}-\frac{∂v}{∂y}) dx dy \)
\(= ∬_R(\frac{-∂v}{∂x}+\frac{∂v}{∂x})dx dy + i ∬_R(\frac{∂v}{∂y}-\frac{∂v}{∂y})dx dy\)
Using C-R conditions \( \frac{∂u}{∂x} = \frac{∂v}{∂y} and \frac{∂u}{∂y} = -\frac{∂v}{∂x}\)
∫C f(z) dz = 0
2. Which of the following theorems can be applied in the function of Cauchy’s Integral Theorem?
a) Green’s Theorem
b) Stokes Theorem
c) Gauss Divergence Theorem
d) Taylors Theorem
View Answer
Explanation: Let us consider f (z) = u (x, y) + i v (x, y)
As f’(z) is continuous, the four partial derivatives \( \frac{∂u}{∂x},\frac{∂u}{∂y},\frac{∂v}{∂x},\frac{∂v}{∂y}\) are also continuous in R and C.
Hence we can apply Green’s Theorem for a plane.
\(∫_C(Pdx+Qdy)= ∬_R(\frac{∂Q}{∂x}-\frac{∂P}{∂y}) dx dy \)
And thus we obtain the equation
\(∫_Cf (z)dz= ∬_R(-\frac{∂v}{∂x}-\frac{∂u}{∂y})dx dy+ i ∬_R(\frac{∂u}{∂x}-\frac{∂v}{∂y}) dx dy\)
3. If there are finite number of simple closed curves C1, C2 … Cn inside C and f (z) is analytic in the region within the regions between the curves C1, C2 … Cn, then
\(∫_Cf(z)dz= ∫_{C1}f(z)dz+ ∫_{C2}f(z)dz+⋯+∫_{Cn}f(z)dz\)
a) True
b) False
View Answer
Explanation: This can be explained by Cauchy’s theorem for Multi connected Region. Let us consider the following Multi connected region.
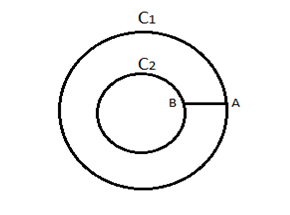
Make a cut AB to convert Multi connected Region to Simply connected region. Then according to Cauchy’s Integral Theorem,
\( ∫_{C1AB C2BA}f(z)dz=0 \) \( ∫_{C1}f(z)dz+∫_{AB}f(z)dz+ ∫_{C2}f(z)dz+∫_{BA}f(z)dz=0 \)
\(∫_{AB}f(z)dz= -∫_{BA}f(z)dz \)
If the path of curves is in the same direction,
\(∫_{C1}f(z)dz- ∫_{C2}f(z)dz=0 \)
\(∫_{C1}f(z)dz= ∫_{C2}f(z)dz\)
4. Which of the following is obtained by evaluating \(∫_C(z-3)^ndz\), where C is |z-3|=9?
a) -1
b) 2
c) 1
d) 0
View Answer
Explanation: Let f (z) = (z-3)n
We know that f (z) is analytic inside and on C.
Therefore, by Cauchy’s Integral Theorem,
We get \(∫_C(z-3)^n dz=0\)
5. Which of the following can be obtained by evaluating \(∫_C\frac{e^{3z}}{z^2+1}dz\), where C is |z|= 1/2?
a) 0
b) 1
c) -1
d) ∞
View Answer
Explanation: Given: \(∫_C\frac{e^{3z}}{z^2+1}dz\)
z2+1=0; z2=-1
Hence, z = ± i both lies outside C
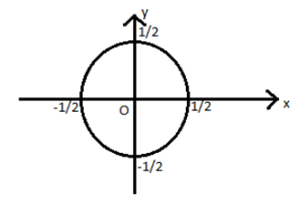
Hence, by Cauchy’s Integral theorem,
\(∫_C\frac{e^{3z}}{z^2+1}dz=0\)
6. Cauchy’s Integral theorem is applicable only for a simply connected region R enclosed by a curve C.
a) True
b) False
View Answer
Explanation: The multi connected region is converted into a simply connected region because Cauchy’s Integral Theorem is applicable only for a simply connected region. For example, let us consider the figure below.
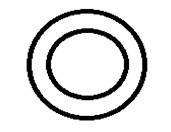
The above multi connected region is converted into a simply connected region as shown below.
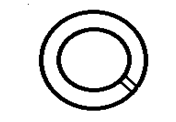
Hence, for this simply connected region, Cauchy’s Integral Theorem can be applied.
7. For which of the following functions, the Cauchy’s Integral Theorem cannot be applied?
a) \(F (z) = \sqrt{|xy|} \)
b) \(F (z) = \frac{e^2z}{1+z^2} \)
c) \(F (z) = (z -2)^n \)
d) \(F (z) = \tan(z) \)
View Answer
Explanation: \(F (z) = \sqrt{|xy|}\) is not analytic inside and on C even though C-R equation is satisfied.
F(z) = tan(z) is analytic except at \(z= ±\frac{π}{2}, ±\frac{3π}{2}\) …
All these points lie outside C. f’(z) is continuous inside C.
Hence, by Cauchy’s integral Theorem,
\(∫_Cf (z) dz=0\)
8. If C is a point on the arc joining a and b, then which of the following equation is correct?
a) \(∫_a^bf(z)dz= ∫_a^cf(z)dz+ ∫_c^bf(z)dz\)
b) \(∫_a^bf(z)dz= ∫_c^af(z)dz+ ∫_a^bf(z)dz\)
c) \(∫_a^bf(z)dz= ∫_b^cf(z)dz+ ∫_c^af(z)dz\)
d) \(∫_a^bf(z)dz= ∫_a^bf(z)dz+ ∫_b^cf(z)dz\)
View Answer
Explanation: If C is a point on the arc joining a and b, it can be reduced into two line integrals as shown below.
\( ∫_a^bf(z)dz= ∫_a^cf(z)dz+ ∫_c^bf(z)dz\)
This integral along a simple closed curve can be specifically called as Contour Integral.
9. For which of the following functions, the Cauchy’s Integral theorem can be applied?
a) \(F (z) = e^x (cosy+i \,siny)\)
b) \(F (z) = e^x (cosy-i \,siny)\)
c) \(F (z) = \frac{x-iy}{2y^2} \)
d) \(F (z) = x^2 – y^2 + 2i \,x \,y\)
View Answer
Explanation: Consider the function F (z) = (x2 – y2 + 2i x y)
\(∫_C(x^2-y^2+2i \,x \,y)dz=∫_C(x+iy)^2 dz = ∫_Cz^2dz \) Let f (z) = z2
Then, f (z) is analytic inside and on C. f’ (z) is continuous inside C.
Hence by Cauchy’s integral Theorem,
\(∫_Cf (z)dz=0\) Other given functions are non-analytic and hence, Cauchy’s Integral Theorem cannot be applied.
10. Which of the following values can be obtained by evaluating the integral \(∫_C\frac{z+4}{5+2z+z^2} \), where C is the circle |z+1| = 1?
a) 1
b) ∞
c) -1
d) 0
View Answer
Explanation:
The Radius of the given Circle is 1.
To find the centre, z +1 = z = -1
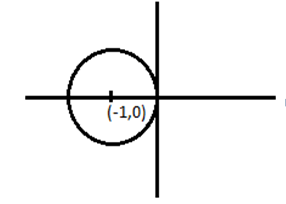
To find the poles,
z2 + 2z + 5 = 0
\(z = \frac{-2 ± \sqrt{(4)}-20}{2} = \frac{-2±4i}{2} =-1 ± 2i\)
This value of poles corresponds to y axis. Hence, by Cauchy’s Integral Theorem,
\(∫_C\frac{z+4}{5+2z+z^2} = 0 \)
Sanfoundry Global Education & Learning Series – Complex Integration.
To practice all areas of Complex Integration, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Numerical Methods MCQ
- Check Engineering Mathematics Books
- Apply for 1st Year Engineering Internship
- Practice Probability and Statistics MCQ
