This set of Ordinary Differential Equations Multiple Choice Questions & Answers (MCQs) focuses on “First Order Nonlinear Differential Equations”.
1. Find the solution for \(\lim_{x\to 0} \frac{ax}{ax+x}.\)
a) 0
b) a
c) 1
d) \(\frac{a}{a+1}\)
View Answer
Explanation: The given equation can be solved using L-Hospital’s Rule,
\(\frac{d(ax)}{dx}=a, \frac{d(ax+x)}{dx}=a+1\)
\(\lim_{x\to 0}\frac{ax}{ax+x} → \lim_{x\to 0}\frac{a}{a+1} → \frac{a}{a+1}\)
2. A rectangular frame is to be made of 240 cm long. Determine the value of the length of the rectangle required to maximize the area.
a) 24 cm
b) 60 cm
c) 240 cm
d) 120 cm
View Answer
Explanation: Let us consider ‘x’ as length and ‘y’ as the breadth of the rectangle.
Given: Perimeter 2(x + y) = 240 cm
x + y = 120
y = 120 – x
Area of the rectangle, a = x*y = x(120-x) = 120x – x2
Finding the derivative, we get, \(\frac{d(a)}{dx}= \frac{d(120x- x^2)}{dx}=120-2x \)
To find the value of x that maximizes the area, we substitute \(\frac{d(a)}{dx}= 0.\)
Therefore, we get, 120 – 2x =0
2x = 120
x = 60 cm
To check if x = 60 cm is the value that maximizes the area, we find the second derivative of the area,
\(\frac{d^2 (a)}{dx^2}= -2\) < 0 …………………. (i)
We know that the condition for maxima is \(\frac{d^2 (f(x))}{dx^2}<0,\) which is satisfied by (i), therefore, x = 60 cm maximizes the area of the rectangle.
3. Find the solution of the system using Gauss Elimination method.
x – y + 2z = 8 y – z = 4 2x + 3z = 2
a) x = 18, y = -18, z = -22
b) x = -12, y = -18, z = 22
c) x = 34, y = -18, z = -22
d) x = -18, y = -12, z = 22
View Answer
Explanation: Augmented Matrix of the given system is,
\( \left[ \begin{array}{ccc|c}
1 & -1 & 2 & 8 \\
0 & 1 & -1 & 4 \\
2 & 0 & 3 & 2
\end{array} \right]\)
Now, applying the steps for Gauss Elimination method (making the elements below the diagonal zero), we get,
\( \left[ \begin{array}{ccc|c}
1 & -1 & 2 & 8 \\
0 & 1 & -1 & 4 \\
2 & 0 & 3 & 2
\end{array} \right] \quad ^{\underrightarrow{R3 \rightarrow R3 – 2R1}} \)
\( \left[ \begin{array}{ccc|c}
1 & -1 & 2 & 8 \\
0 & 1 & -1 & 4 \\
0 & 2 & -1 & -14
\end{array} \right] \quad ^{\underrightarrow{R3 \rightarrow R3 – 2R2}} \)
\( \left[ \begin{array}{ccc|c}
1 & -1 & 2 & 8 \\
0 & 1 & -1 & 4 \\
0 & 0 & 1 & -22
\end{array} \right]\)
Now converting the augmented matrix back to set of equations, we get,
x – y + 2z = 8 …………………………. (i)
y – z = 4 …………………………………. (ii)
z = -22 …………………………………… (iii)
Substituting value of z in (ii), we get,
y + 22 = 4
y = -18
Substituting the value of y and z in (i), we get,
x + 18 + 2(-22) = 8
x – 26 = 8
x = 34
Therefore, the solution of the system is x = 34, y = -18, z = -22.
4. What is the solution of the given equation?
x6y6 dy + (x7y5 +1) dx = 0
a) \(\frac{(xy)^6}{6} + lnx = c \)
b) \(\frac{(xy)^5}{6} + lny = c\)
c) \(\frac{(xy)^5}{5}+ lnx = c\)
d) \(\frac{(xy)^6}{6}+ lny = c\)
View Answer
Explanation: Given: (x6y6 + 1) dy + x7y5dx = 0, is an example of non-exact differential equation.
Dividing the equation by x we get,
x5y6 dy + x6y5dx + \(\frac{dx}{x} = 0\)
x5y5 (ydy + xdx) + \(\frac{dx}{x} = 0 \)
(xy)5 (d(xy)) + \(\frac{dx}{x} = 0\)
\(\frac{(xy)^6}{6} + lnx = c \)
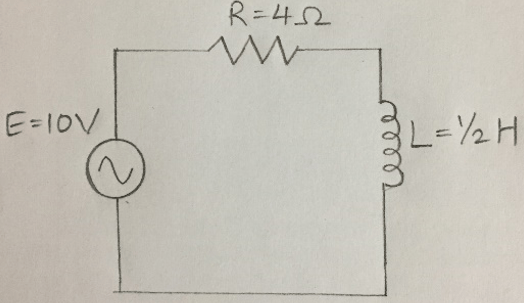
5. Determine the current i(t) for the circuit shown, if the initial current is zero.
a) i(t) = 9 – 9e8t
b) i(t) = 9 – e-8t
c) i(t) = 9 – 9e-8t
d) i(t) = 8 – 9e-8t
View Answer
Explanation: The given circuit is an application of First Order Differential equations (R-L Circuit).
Hence, we know that, \(L\frac{di(t)}{dt} + Ri(t) = E(t) \)
\(\frac{1}{2} \frac{di(t)}{dt} + 4i(t) = 10\)
\(\frac{di(t)}{dt} + 8i(t) = 20\) …………………………. (i)
Integrating Factor, \(u(t) = e^{∫8 dt}= e^{8t}\) …………………………… (ii)
Applying (ii) on both sides of (i) we get,
\(e^{8t}.\frac{di(t)}{dt} + e^{8t}. 8i(t) = 72 e^{8t} \)
\(\frac{d(e^{8t}.i(t))}{dt} = 72 e^{8t} \)
Integrating on both sides we get,
\(∫\frac{d(e^{8t}.i(t))}{dt} = ∫72 e^{8t}.dt\)
\(e^{8t} .i(t) = \frac{72}{8} .e^{8t} + c\)
i(t) = 9 + ce-8t
Given: i(0) = 0
i(0)= 9 + ce-8(0) = 0
c = -9
Therefore, i(t) = 9 – 9e-8t
6. \(xy^3(\frac{dy}{dx})^2+yx^2+\frac{dy}{dx}=0\) is a _____________
a) Second order, third degree, linear differential equation
b) First order, third degree, non-linear differential equation
c) First order, third degree, linear differential equation
d) Second order, third degree, non-linear differential equation
View Answer
Explanation: Since the equation has only first derivative, i.e. \((\frac{dy}{dx}),\) it is a first order equation.
Degree is defined as the highest power of the highest order derivative involved. Hence it is 2.
The equation has one/more terms having a variable of degree two/higher; hence it is non-linear.
7. Which of the following is one of the criterions for linearity of an equation?
a) The dependent variable and its derivatives should be of second order
b) The dependent variable and its derivatives should not be of same order
c) Each coefficient does not depend on the independent variable
d) Each coefficient depends only on the independent variable
View Answer
Explanation: The two criterions for linearity of an equation are:
The dependent variable y and its derivatives are of first degree.
Each coefficient depends only on the independent variable
8. Beta function is not a symmetric function.
a) True
b) False
View Answer
Explanation: Beta function is a symmetric function, i.e.,
β(x,y) = β(y,x), where x>0 and y>0.
9. Which of the following is the property of error function?
a) erf (0) = 1
b) erf (∞) = 1
c) erf (0) = ∞
d) erf (∞) = 0
View Answer
Explanation: Error Function is given by, \(erf(x) = \frac{2}{\sqrt π} ∫_0^xe^{-t^2}dt. \)
Some of its properties are:
erf (0) = 0
erf (∞) = 1
erf (-x) = -erf(x)
10. The equation \(2\frac{dy}{dx} – xy = y^{-2},\) is an example for Bernoulli’s equation.
a) False
b) True
View Answer
Explanation: A first order, first degree differential equation of the form,
\(\frac{dy}{dx} + P(x). y = Q(x). y^a,\) is known as Bernoulli’s equation.
Sanfoundry Global Education & Learning Series – Ordinary Differential Equations.
To practice all areas of Ordinary Differential Equations, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Probability and Statistics MCQ
- Apply for 1st Year Engineering Internship
- Practice Numerical Methods MCQ
- Check Engineering Mathematics Books
