This set of Differential and Integral Calculus Multiple Choice Questions & Answers (MCQs) focuses on “Total Derivative”.
1. The total derivative is the same as the derivative of the function.
a) True
b) False
View Answer
Explanation: In mathematics, the total derivative of a function at a point is the best linear approximation near this point of the function with respect to its arguments.
2. What is the derivative of \(7\sqrt[3]{x}-\frac{3}{x^4}+5x\) with respect x?
a) \(7x^{\frac{-1}{3}}-3x^{-5}+5\)
b) \(7x^{\frac{-2}{3}}-3x^{-5}+5\)
c) \(7x^{\frac{-2}{3}}-3x^{-3}+5\)
d) \(7x^{\frac{-1}{3}}-3x^{-3}+5\)
View Answer
Explanation: Given: y= \(7\sqrt[3]{x}-\frac{3}{x^4}+5x\)
\(\frac{dy}{dx}=\frac{d(7x^{\frac{-1}{3}}-3x^{-4}+5x)}{dx}\)
\(\frac{dy}{dx}=7x^{\frac{-1}{3}-1}-3x^{-4-1}+5x^{1-1}\)
\(\frac{dy}{dx}=7x^{\frac{-2}{3}}-3x^{-5}+5\)
3. Find the range in which the function f(x) = 8 + 40x3 – 5x4 – 4x5 is increasing.
a) 2<z<0, 0<z<3
b) 1<z<0, 0<z<2
c) 3<z<0, 0<z<2
d) 3<z<0, 0<z<4
View Answer
Explanation: Given: f(x)=8 + 40x3 – 5x4 – 4x5
f'(x) = 120x2 – 20x3 – 20x4
f'(x) = -20x2 (x+x2 – 6)
f'(x) = -20x2 (x+3)(x-2)
Next, we need to know where the function is not changing and so all we need to do is set the derivative equal to zero and solve.
f'(x) = -20x2 (x+3)(x-2)=0
From this it is pretty easy to see that the derivative will be zero, and hence the function will not be moving, at,
x=0,-3,-2
Because the derivative is continuous, we know that the only place it can change sign is where the derivative is zero. So, a quick number line will give us the sign of the derivative for the various intervals.
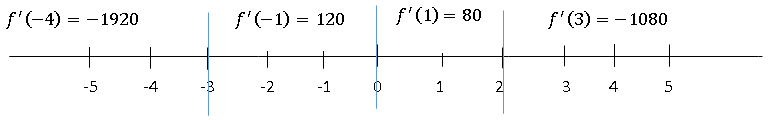
From this we get,
Increasing: 3<z<0, 0<z<2
4. What is the maximum area of the rectangle with perimeter 500 mm?
a) 15,625 mm2
b) 15,025 mm2
c) 15,600 mm2
d) 10,625 mm2
View Answer
Explanation: Let x be the length of the rectangle and y be the width of the rectangle. Then, Area A is,
A=x*y …………………………………………………. (1)
Given: Perimeter of the rectangle is 620 mm. Therefore,
P=2(x+y)
500=2(x+y)
x+y=250
y=250-x
We can now substitute the value of y in (1)
A=x*(250-x)
A=250x-x2
To find maximum value we need derivative of A,
\(\frac{dA}{dx}=250-2x\)
To find maximum value, \(\frac{dA}{dx}=0\)
250-2x=0
2x=250
x=125 mm
Therefore, when the value of x=125 mm and the value of y=250-125=125 mm, the area of the rectangle is maximum, i.e., A=125*125=15,625 mm2
5. Which of the following relations hold true?
a) i × i = j × j = k × k = 1
b) i × j = k, j × i = -k
c) i × i = j × j = k × k = -1
d) k × i = -j, i × k = j
View Answer
Explanation: The properties of vector or cross product, for the orthogonal vectors, i, j, and k are,
i × i = j × j = k × k = 0,
i × j = k, j × i = -k,
j × k = i, k × j = -i,
k × i = j, i × k = -j
6. Which of the following trigonometric function derivatives is correct?
a) \(\frac{d(sinx)}{dx}=-cosx\)
b) \(\frac{d(secx)}{dx}=tanx\)
c) \(\frac{d(tanx)}{dx}=sec^2 x\)
d) \(\frac{d(cosx)}{dx}=sinx\)
View Answer
Explanation: Correct forms of Trigonometric Derivative Functions
- \(\frac{d(sinx)}{dx}=cosx\)
- \(\frac{d(cosx)}{dx}=-sinx\)
- \(\frac{d(secx)}{dx}=secxtanx\)
- \(\frac{d(tanx)}{dx}=sec^2 x\)
7. The division rule of differentiation for two functions is given by, \((\frac{f(x)}{g(x)})’= \frac{f'(x)-g’ (x)}{(g(x))^2}. \)
a) True
b) False
View Answer
Explanation: The division rule of differentiation for two functions is given by,
\((\frac{f(x)}{g(x)})’= \frac{g(x)f'(x)- g'(x)f(x)}{(g(x))^2} \)
8. What is the derivative of z=3x*logx+5x6 ex with respect to x?
a) 3+30x5 ex
b) 3+5x6 ex+30x5 ex
c) 3+5x6 ex
d) 3+3logx+5x6 ex+30x5 ex
View Answer
Explanation: Given: z=3x*logx+5x6 ex
\(\frac{dz}{dx}=3x(\frac{1}{x})\)+3logx+5x6 ex+30x5 ex
\(\frac{dz}{dx}\)=3+3logx+5x6 ex+30x5 ex
9. A sphere with the dimensions is shown in the figure. What is the error that can be incorporated in the radius such that the volume will not change more than 2%?
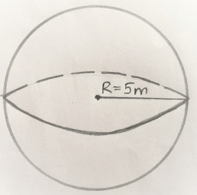
a) 0.06366%
b) 0.006366%
c) 0.6366%
d) 6.366%
View Answer
Explanation: We know that volume of the sphere is,
\(V = \frac{4}{3} πR^3 \)
Differentiating the above equation with respect to R we get,
\(\frac{dV}{dR}= \frac{4}{3} π×3R^2=4πR^2\)
Since the volume of the sphere should not exceed more than 2%,
\(dR=\frac{dV}{4πR^2}=\frac{0.02}{4π(5)^2}=0.00006366\)
Error in radius = 0.006366%
10. Which of the following is correct?
a) \(\frac{d}{dx} (sin^{-1}(x)) = \frac{1}{\sqrt{1-x}}\)
b) \(\frac{d}{dx} (sec^{-1}(x)) = \frac{1}{x\sqrt{x^2-1}}\)
c) \(\frac{d}{dx} (tan^{-1}(x)) = \frac{1}{\sqrt{x^2+1}}\)
d) \(\frac{d}{dx} (sin^{-1}(x)) = \frac{1}{x+1} \)
View Answer
Explanation: Rules for derivatives of inverse trigonometric functions are:
- \(\frac{d}{dx} (sin^{-1}(x)) = \frac{1}{\sqrt{1-x^2}}\)
- \(\frac{d}{dx} (sec^{-1}(x)) = \frac{1}{x\sqrt{x^2-1}}\)
- \(\frac{d}{dx} (tan^{-1}(x)) = \frac{1}{1+x^2}\)
Sanfoundry Global Education & Learning Series – Differential and Integral Calculus.
To practice all areas of Differential and Integral Calculus, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Engineering Mathematics Books
- Practice Numerical Methods MCQ
- Practice Probability and Statistics MCQ
- Apply for 1st Year Engineering Internship
