This set of Ordinary Differential Equations Multiple Choice Questions & Answers (MCQs) focuses on “Geometrical Applications”.
1. Who invented the rectangular coordinate system?
a) Frans van Schooten
b) René Descartes
c) Isaac Newton
d) Gottfried Wilhelm Leibniz
View Answer
Explanation: The rectangular coordinate system was invented by French mathematician and philosopher René Descartes, who published this idea in 1637.
2. What is the formula for the intercept of tangent line on x-axis?
a) \(x-\frac{y}{y’}\)
b) \(y-\frac{x}{y’}\)
c) y – xy’
d) y – x’y
View Answer
Explanation: Intercept of a tangent line on the:
x-axis: \(x-\frac{y}{y’}\)
y-axis: y – xy’
3. The intercept of a normal line on y axis is given by, \(y+\frac{x}{y’}.\)
a) True
b) False
View Answer
Explanation: Intercept of a normal line on the:
x-axis: x + yy’
y-axis: \(y+\frac{x}{y’}\)
4. What is the time taken by the particle to cover a distance of 98 meters, if the particle is moving with a velocity given by, \(\frac{dx}{dt}= \frac{1}{x} \) (x is the distance)?
a) 48 s
b) 50 s
c) 98 s
d) 49 s
View Answer
Explanation: Given: \(\frac{dx}{dt}= \frac{1}{x} \)
dt=xdx
Integrating, \(∫dt=∫_0^{98}xdx\)
\(t= (\frac{x^2}{2})_0^{98}=\frac{98}{2}=49 s\)
5. Which of the following relations hold true?
a) i × i = j × j = k × k = 1
b) i × j = -k, j × i = k
c) i × i = j × j = k × k = 0
d) k × i = -j, i × k = j
View Answer
Explanation: One of the properties of vector or cross product is, for the orthogonal vectors, i, j, and k, we have the relation,
i × i = j × j = k × k = 0,
i × j = k, j × i = -k,
j × k = i, k × j = -i,
k × i = j, i × k = -j
6. In recurrence relation, each further term of a sequence or array is defined as a function of its succeeding terms.
a) True
b) False
View Answer
Explanation: An equation that gives a sequence such that each next term of the sequence or array is defined as a function of its preceding terms, is called a recurrence relation.
7. What is the maximum area of the rectangle with perimeter 650 mm?
a) 26,406.25 mm2
b) 26,406 mm2
c) 24,000 mm2
d) 24,075 mm2
View Answer
Explanation: Let x be the length of the rectangle and y be the width of the rectangle. Then, Area A is,
A=x*y …………………………………………………. (1)
Given: Perimeter of the rectangle is 620 mm. Therefore,
P=2(x+y)
650=2(x+y)
x+y=325
y=325-x
We can now substitute the value of y in (1)
A=x*(325-x)
A=325x-x2
To find maximum value we need derivative of A,
\(\frac{dA}{dx}=325-2x\)
To find maximum value, \(\frac{dA}{dx}=0\)
325-2x=0
2x=325
x=162.5 mm
Therefore, when the value of x=162.5 mm and the value of y=325-162.5=162.5 mm, the area of the rectangle is maximum, i.e., A=162.5*162.5=26,406.25 mm2
8. What is the derivative of z=3x*logx+5x6 with respect to x?
a) 3+30x5 ex
b) 3+5x6 ex+30x5 ex
c) 3+5x6 ex
d) 3+3logx+30x5 ex
View Answer
Explanation: Given: z = 3x*logx+5x6 ex
\(\frac{dz}{dx}=3x(\frac{1}{x})\)+3logx+30x5 ex
\(\frac{dz}{dx}\) = 3+3logx+30x5 ex
9. A sphere with the dimensions is shown in the figure. What is the error that can be incorporated in the radius such that the volume will not change more than 10%?
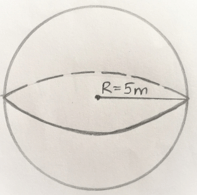
a) 0.3183%
b) 0.03183%
c) 31.83%
d)3.183%
View Answer
Explanation: We know that volume of the sphere is,
\(V = \frac{4}{3} πR^3 \)
Differentiating the above equation with respect to R we get,
\(\frac{dV}{dR}= \frac{4}{3} π×3R^2=4πR^2 \)
Since the volume of the sphere should not exceed more than 10%,
\(dR=\frac{dV}{4πR^2}=\frac{0.1}{4π(5)^2}=0.0003183\)
Error in radius = 0.03183%
10. What is the degree of the differential equation, x3-6x3y3+2xy=0?
a) 3
b) 5
c) 6
d) 8
View Answer
Explanation: The degree of an equation that has not more than one variable in each term is the exponent of the highest power to which that variable is raised in the equation. But when more than one variable appears in a term, it is necessary to add the exponents of the variables within a term to get the degree of the equation. Hence, the degree of the equation, x3-6x3y3+2xy=0, is 3+3 = 6.
Sanfoundry Global Education & Learning Series – Ordinary Differential Equations.
To practice all areas of Ordinary Differential Equations, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Engineering Mathematics Books
- Practice Probability and Statistics MCQ
- Practice Numerical Methods MCQ
- Apply for 1st Year Engineering Internship
