This set of Differential and Integral Calculus Multiple Choice Questions & Answers (MCQs) focuses on “Standard Curves in Cartesian Form”.
1. In geometry, the folium of Descartes is an algebraic curve defined by the equation
x3+y3+3xy=0.
a) True
b) False
View Answer
Explanation: The curve was first proposed by Descartes in 1638. It is defined by the equation,
x3+y3-3xy=0.
2. Which of the following represents the polar equation of Cissoid of Diocles?
a) r=2a*tanθ*sinθ
b) r=a*tanθ*sinθ
c) r=a*tanθ*cosθ
d) r=2ax*tanθ*sinθ
View Answer
Explanation: The curve of Cissoid was invented by Diocles in about 180 BC. The curve is given by,
Cartesian Equation: \(y^2=\frac{x^3}{(2a-x)} \)
Polar Equation: r=2a*tanθ*sinθ
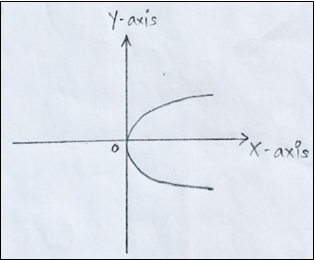
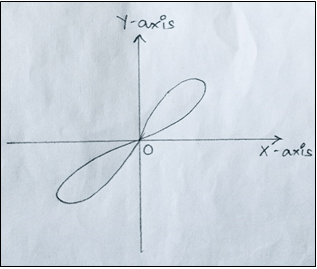
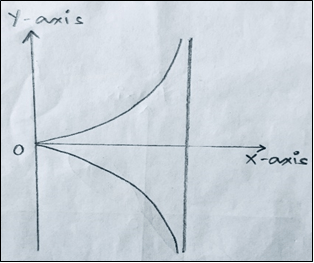
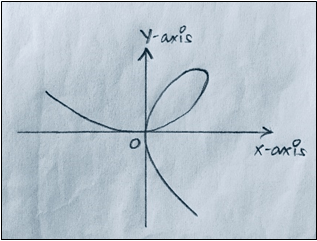
3. Which of the following represents the graph of Cissoid of Diocles?
a)
b)
c)
d)
View Answer
Explanation: The Cissoid curve (meaning ivy-shaped) was invented by Diocles in connection with his attempt to duplicate the cube by geometrical methods. If the cusp of the cissoid is taken as the center of inversion, the cissoid inverts to a parabola.
4. Which of the following represents the correct cartesian equation for Lemniscate of Bernoulli?
a) (x2+y2)2=2a2 (x2-y2)
b) (x2+y)2=2a2 (x2-y2)
c) (x2+y2)2=2(x2-y2)
d) (x2+y2)2=a2 (x2-y2)
View Answer
Explanation: The Lemniscate of Bernoulli was first described as a modification of an ellipse in 1694 by Jakob Bernoulli. It is represented as,
Cartesian Equation: (x2+y2)2=2a2 (x2-y2)
Polar Equation: r2=2a2*cos2θ
5. The polar coordinates of strophoid is given by
\(r=f(θ)±\sqrt{(f(θ)cosθ-a)^2+(f(θ)sinθ-b)^2}. \)
a) False
b) True
View Answer
Explanation: The strophoid is a special case of cissoid and is usually defined as a looping curve. It was first studied by Issac Barrow (October 1630 – 4 May 1677) in 1670.
6. What are the tangents to the curve y2=4ax at the origin?
a) x=0
b) x=0, y=0
c) y=0
d) x=y
View Answer
Explanation: Given: y2=4ax
To find the tangent to the curve at the origin, we need to equate the lowest degree term to 0.
Therefore, 4ax=0, which gives x=0.
7. At the point where \(\frac{dy}{dx}=∞,\) the tangent is parallel to y axis.
a) False
b) True
View Answer
Explanation: At the point where \(\frac{dy}{dx}=0,\) the tangent is parallel to x axis, i.e., horizontal. At the point where \(\frac{dy}{dx}=∞,\) the tangent is vertical, i.e., parallel to y axis.
8. Which of the following is not correct regarding Folium of Descartes?
a) The equation is third degree in both x and y
b) Its asymptote is given by x+y+a=0
c) It is symmetrical about y = x
d) It forms a loop in the second quadrant
View Answer
Explanation:
- The Folium of Descartes is an algebraic curve defined as, x3+y3-3xy=0.
- It is symmetrical about y = x.
- It forms a loop in the first quadrant with a double point at the origin and asymptote, x+y+a=0.
9. What is the value of the given limit, \(\lim_{x\to 0}\frac{25}{x}\)?
a) 25
b) 0
c) \(\frac{1}{2}\)
d) \(\frac{3}{2}\)
View Answer
Explanation: Given: \(\lim_{x\to 0}\frac{25}{x}\)
Using L’Hospital’s Rule, by differentiating both the numerator and denominator with respect to x,
\(\lim_{x\to 0}\frac{25}{1} = 25.\)
10. Vertical asymptotes are parallel to both x and y axes.
a) True
b) False
View Answer
Explanation: Oblique asymptotes are those which are neither parallel to x-axis nor y-axis and are given by y=mx+c where \(m=\lim_{x\to ∞}(\frac{x}{y})=\lim_{x\to ∞}(y-mx).\)
Sanfoundry Global Education & Learning Series – Differential and Integral Calculus.
To practice all areas of Differential and Integral Calculus, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Engineering Mathematics Books
- Practice Numerical Methods MCQ
- Apply for 1st Year Engineering Internship
- Practice Probability and Statistics MCQ
