Mapping w = z^2 - Complex Analysis Questions and Answers

This set of Complex Analysis Multiple Choice Questions & Answers (MCQs) focuses on “Mapping w = z^2”.

1. Which of the following is the image of the hyperbola x²-y²=10 under the transformation w= z² if w = u + i v?
a) u=10
b) u=15
c) u=30
d) u=20
View Answer

Answer: a
Explanation:
w= z²
u+iv= (x+iy)²
= x²– y²+ i2xy
i.e. u= x²-y²…………(1)
v=2xy…………(2)
Given: x²-y²=10
u=10
Hence, the image of the hyperbola x²– y²=10 in the z plane is mapped into u=10 in the w plane, which is a straight line.

2. Which of the following regions is the region of w plane into which the circle |z-1|= 1 is mapped by the transformation w= z² ?
a) R=2[1+sin⁡∅]
b) R=[1+sin⁡∅]
c) R=[1+cos⁡∅]
d) R=2[1+cos⁡∅]
View Answer

Answer: d
Explanation:
In polar form,z =r e^iθ, w = R e^iφ
Given: |z-1|= 1
i.e.|re^iθ-1|=1
|rcos⁡θ+ irsin⁡θ-1|=1
|(rcos⁡θ-1)+ irsin⁡θ|=1
(rcos⁡θ-1)²+ (rsin⁡θ)²= 1²
r²cos²θ+ 1- 2rcos⁡θ+ r²sin² θ=1
r² [cos²θ+ sin²θ]= 2rcos⁡θ
r²=2rcos⁡θ
r=2 cos⁡θ…………(1)
Given: w= z²
Re^(i∅)= (re^iθ)²
Re^i∅=r² e^i2θ
R= r², ∅=2θ…………(2)
(1)→ r²= (2cos⁡θ)²
r²=4cos²θ
=4 \([\frac{1+cos⁡2θ}{2}] \)
r²=2[1+cos⁡2θ]
R=2 [1+cos∅] (From (2))

3. Which of the following images is an image under the mapping w=z² of the triangular region bounded by y=1, x=1 and x+y= 1?
a) \( u^2= -2(v-\frac{1}{2}) \)
b) \( u^2=2(v- \frac{1}{2}) \)
c) \( u^2=(v- \frac{1}{2}) \)
d) \( u^2=(v+ \frac{1}{2}) \)
View Answer

Answer: a
Explanation:
In Z plane, given lines are x=1, y=1, x+y=1
Given: w= z²
u+iv= (x+iy)²
u+iv= x²– y²+ 2xyi
Equating the real and imaginary parts, we get
u= x²– y²…………(1)
v=2 xy…………(2)

When x=1	When y=1
(1)→u=1- y²…(3) (2)→v=2y…(4)	(1)→u= x²-1…(5) (2)→v=2x…(6)
(4)→v²=4y² v²=4(1-u) by (3) i.e. v²=-4(u-1)	(6)→ v²= 4x² =4(u+1) by(5)

When x + y =1
(1) →u= (x+y)(x-y)
u=x-y [x+y=1] \(u= \sqrt{(x+y)^2-4xy}\) (Identity)
\(u= \sqrt{1-2v} \)
\(u^2=1-2v = -2 (v-\frac{1}{2}) \)
The image of x =1 is v²= -4(u-1)
The image of y =1 is v²=4(u+1)
The image of x+y=1 is \(u^2= -2(v-\frac{1}{2}) \)

4. Which of the following images is an image of |z-2i| = 2 under the transformation \(w= \frac{1}{z} \)?
a) \(v= \frac{-1}{2} \)
b) \(v= \frac{1}{2} \)
c) \(v= \frac{-1}{4} \)
d) \(v= \frac{1}{4} \)
View Answer

Answer: c
Explanation:
Given:|z-2i|= 2……(1) is a circle
Centre = 2i i.e., (0,2)
Radius=2
Given: \(w=\frac{1}{z}→z= \frac{1}{w} \)

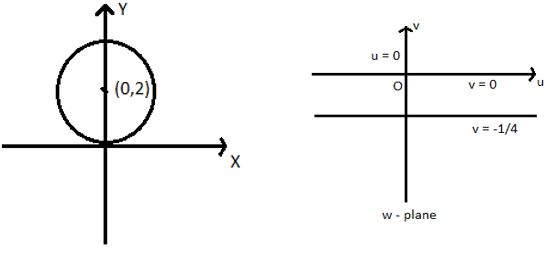
\((1)→|\frac{1}{w}-2i|= 2 \)
|1-2wi|= 2|w|
|1-2(u+iv)i|= 2 |u+iv|
|1-2ui+2v|= 2|u+vi|
|1+2v-2ui|= 2 |u+iv|
\(\sqrt{(1+2v)^2+(-2u)^2}=2 \sqrt{u^2+v^2} \)
\((1+2v)^2+ 4u^2= 4(u^2+ v^2) \)
1+4v=0
\(v=\frac{-1}{4}\), which is a straight line in w-plane.

Note: Join free Sanfoundry classes at Telegram or Youtube

5. Which of the following images is the image of the circle |z-1|=1 in the complex plane under the mapping \(w= \frac{1}{z}? \)
a) \(u=\frac{-1}{2} \)
b) \(u= \frac{1}{2} \)
c) \(u= \frac{-1}{4} \)
d) \(u= \frac{1}{4} \)
View Answer

Answer: b
Explanation:
Given: |z-1|= 1……(1) is a circle
Centre=1, i.e.,(1,0)
Radius=1
Given: \(w= \frac{1}{z}→z= \frac{1}{w} \)

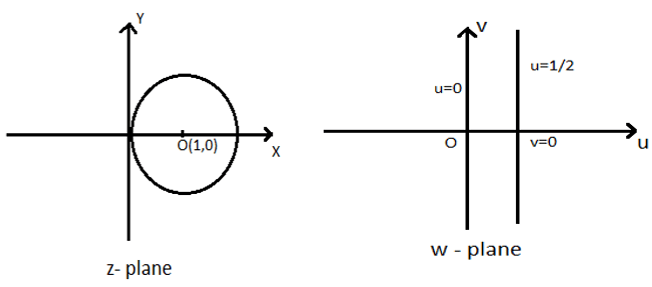
\((1)→|\frac{1}{w}-1|=1 \)
|1-w|=|w|
|1-(u+iv)|=|u+iv|
|1-u-iv|=|u+iv|
\(\sqrt{√(1-u)^2+(-v)^2} = \sqrt{u^2+v^2} \)
\((1-u)^2+ v^2 = u^2 + v^2 \)
\(1+u^2- 2u+ v^2= u^2+ v^2 \)
2u=1
\(u=\frac{1}{2},\) which is a straight line in the w-plane.

6. Which of the following images is an image of the infinite strips 1/4<y<1/2 under the transformation w = 1/z?
a) Region between circle of centre(0,-2)and radius 2 and circle of centre (0,-1) and unit radius
b) Region between circle of centre(0,2) and radius 2 and circle of centre (0,1) and unit radius
c) Region between circle of centre(0,1) and radius 1 and circle of centre (0,-1)and unit radius
d) Region between circle of centre(1,0) and radius 1 and the circle of centre (2,0) and radius 2
View Answer

Answer: a
Explanation:
\(w= \frac{1}{z} (Given) \)
i.e., \( z= \frac{1}{w} \)
\(z= \frac{1}{u+iv}= \frac{u-iv}{(u+iv)(u-iv)}= \frac{u-iv}{u^2+v^2} \)
\(x+iy= \frac{u-iv}{u^2+v^2}= [\frac{u}{u^2+v^2}] + i [\frac{-v}{u^2+v^2}] \)
i.e., \(x= \frac{u}{u^2+v^2}…(1), y=\frac{-v}{u^2+v^2}…(2) \)
Given strip is 1/4 \(u^2+v^2+4v=0 \)
\(u^2+(v+2)^2-4=0 \)
\(u^2+(v+2)^2=4 \) …(3)
It is a circle whose centre is (0,-2)in the w-plane and radius is 2
When y= 1/2
\(\frac{1}{2}= \frac{-v}{u^2+v^2} by (2) \)
\(u^2+v^2= -2v \)
\(u^2+v^2+2v=0 \)
\(u^2+ (v+1)^2-1=0 \)
\(u^2+(v+1)^2=1 \) …(4)
It is a circle whose centre is (0,-1)in the w-plane and unit radius

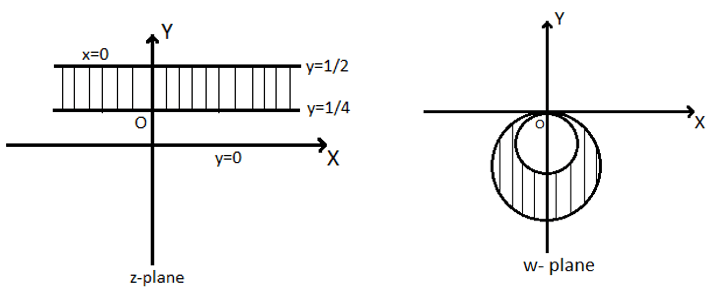
Hence the infinite strip 1/42+(v+1)²=1 and u²+(v+2)²=4 in the w plane.

7. Which of the following images is an image of the infinite strips 0 <y< 1/2 under the transformation w=1/z?
a) Region outside the circle u²+(v+1)²=1
b) Region outside the circle (u-1)²+v²=1
c) Region outside the circle u²+v²=1
d) Region outside the circle (u-1)²+v²=1
View Answer

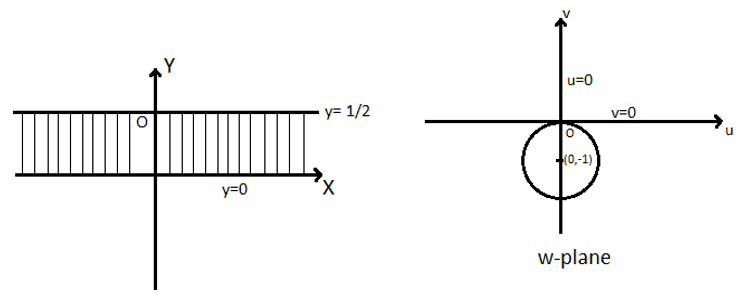
when y=0
→v=0 by (2)
When \( y= \frac{1}{2}, \) we get u²+(v+1)²=1 by (4)
Hence, the infinite strip 0 2+(v+1)²=1 in the lower half of the w-plane.

8. Which of the following is the image of x =2 under the transformation \( w= \frac{1}{z} \)?
a) \( (u-\frac{1}{4})^2+v^2=(\frac{1}{4})^2 \)
b) \((u-\frac{1}{4})^2+(v-1)^2=(\frac{1}{4})^2 \)
c) \((u-\frac{1}{3})^2+v^2=(\frac{1}{4})^2 \)
d) \((u-\frac{1}{2})^2+v^2=(\frac{1}{2})^2 \)
View Answer

Answer: a
Explanation:
Given: \( w= \frac{1}{z} \)
i.e., \( z= \frac{1}{w} \)
\(z= \frac{1}{u+iv}= \frac{u-iv}{(u+iv)(u-iv)}= \frac{u-iv}{u^2+ v^2} \)
\(x+iy=(\frac{u}{u^2+v^2})+ i(\frac{-v}{u^2+ v^2}) \)
i.e., \( x=(\frac{u}{u^2+ v^2})…(1), y=(\frac{-v}{u^2+v^2})…(2) \)
Given: x=2 in the z-plane
\(2= \frac{u}{u^2+v^2} \) by (1)
\(2(u^2+v^2 )= u \)
\(u^2+ v^2-\frac{1}{2} u=0 \)
\((u-\frac{1}{4})^2+ v^2-\frac{1}{16}=0 \)
\((u-\frac{1}{4})^2+v^2=(\frac{1}{4})^2 \)
It is a circle whose centre is (1/4, 0)and radius 1/4.
x=2 in the z-plane is transformed into a circle \((u-\frac{1}{4})^2+v^2=(\frac{1}{4})^2\) in the w-plane.

9. Which of the following is the image of a circle containing the origin in the XY plane under the transformation \( w= \frac{1}{z} \)?
a) A straight line
b) A circle
c) An ellipse
d) A parabola
View Answer

Answer: a
Explanation:
Given:\( w= \frac{1}{z} \)
i.e., \( z= \frac{1}{w} \)
\(z= \frac{1}{u+iv}= \frac{u-iv}{(u+iv)(u-iv)}= \frac{u-iv}{u^2 + v^2} \)
\( x+iy= (\frac{u}{u^2+v^2}+ i(\frac{-v}{u^2+ v^2}) \)
i.e., \(x=(\frac{u}{u^2+ v^2})…(1), y=(\frac{-v}{u^2+v^2})…(2) \)
Given: \(a(x^2+y^2)+bx+cy=0 \)
Substituting (1) and (2), we get
\(a[\frac{u^2}{(u^2+v^2)^2} + \frac{v^2}{(u^2+v^2)^2}]+b[\frac{u}{u^2+v^2}]+ c[\frac{-v}{u^2+v^2}]=0 \)
\(a[\frac{u^2+v^2}{(u^2+v^2)^2}]+\frac{bu-cv}{u^2+v^2}=0 \)
\(a \frac{1}{(u^2+v^2)}+\frac{bu-cv}{u^2+v^2}=0 \)
a+ bu- cv= 0
Therefore, the image of circle passing through the origin in the XY plane is a straight line in the w-plane.

10. Which of the following is the image of 1< x < 2 under the mapping w = 1/z?
a) Region between the circles \((u-\frac{1}{2})^2+v^2=(\frac{1}{2})^2 and (u-\frac{1}{4})^2+v^2=(\frac{1}{4})^2 \)
b) Region between the circles \((u-\frac{1}{2})^2+v^2= 2^2 and (u-\frac{1}{3})^2+v^2= 3^2 \)
c) Region between the circles \((u-\frac{1}{5})^2+v^2= 3^2 and (u-\frac{1}{2})^2+v^2= 4^2 \)
d) Region between the circles \((u-\frac{1}{2})^2+(v-1)^2= (\frac{1}{2})^2 and (u-\frac{1}{4})^2+ (v-2)^2=(\frac{1}{3})^2 \)
View Answer

Answer: a
Explanation:
Given: \( w= \frac{1}{z} \)
i.e., \( z= \frac{1}{w} \)
\(z= \frac{1}{u+iv}= \frac{u-iv}{(u+iv)(u-iv)}=\frac{u-iv}{u^2+v^2} \)
\(x+iy=(\frac{u}{u^2+v^2})+ i (\frac{-v}{u^2+ v^2}) \)
i.e., \(x=(\frac{u}{u^2+ v^2})…(1), y=(\frac{-v}{u^2+v^2})…(2) \)
Given: 1 \(u^2+v^2=u \)
\(u^2+v^2-u=0 \)
\((u-\frac{1}{2})^2+v^2-\frac{1}{4}=0 \)
\((u-\frac{1}{2})^2+v^2=(\frac{1}{2})^2…(3) \)
It is a circle whose centre is (1/2,0) and radius is 1/2
When x = 2
\(2= \frac{u}{u^2+v^2}\, by(1) \)
\(2(u^2+v^2 )= u \)
\(u^2+v^2-\frac{u}{2}=0 \)
\((u-\frac{1}{4})^2+v^2-(\frac{1}{4})^2=0 \)
\((u-\frac{1}{4})^2+v^2= (\frac{1}{4})^2…(4) \)
It is a circle whose centre is \((\frac{1}{4},0)\) and radius is \(\frac{1}{4} \)
Hence the infinite strip 1<x<2 is transformed into the region in between the circles (3) and (4) in the w-plane.

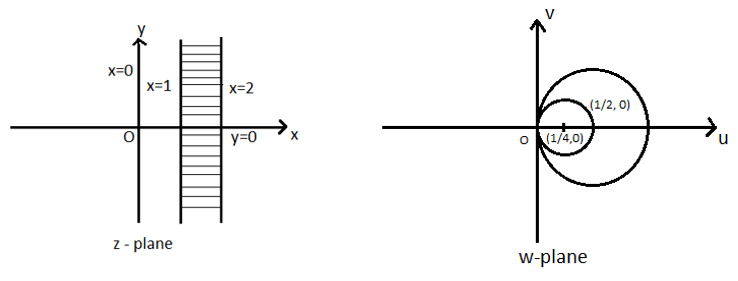
11. Which of the following is the image of the hyperbola x²-y²=1 under the transformation w=1/z?
a) Cardioids
b) Lemniscates
c) Parabola
d) Hyperbola
View Answer

Answer: b
Explanation:
Given:\( w=\frac{1}{z} →z=\frac{1}{w} \)
\(x+iy= \frac{1}{Re^{i∅}} \)
\(x+iy = \frac{1}{R}e^{-i∅}= \frac{1}{R}[cos⁡∅-isin⁡∅] \)
\(x=\frac{1}{R}cos⁡∅, y= \frac{-1}{R} sin⁡∅ \)
Given: x²-y²=1
\([\frac{1}{R}cos⁡∅]^2-[\frac{-1}{R}sin⁡∅]^2=1 \)
\(\frac{cos^2∅-sin^2∅}{R^2} =1 \)
\(cos⁡2∅= R^2 i.e., R^2=cos⁡2∅ \)
It is a lemniscate.

12. The transformation \(w=\frac{1}{z}\) transforms all circles and straight lines in the z-plane into circles or straight lines in the w-plane.
a) True
b) False
View Answer

Answer: a
Explanation:
Given: \(w=\frac{1}{z} \)
i.e., \(z=\frac{1}{w} \)
Now, w= u+iv
\(z= \frac{1}{w}=\frac{1}{u+iv}= \frac{1}{u+iv}\frac{u-iv}{u-iv}= \frac{u-iv}{u^2+v^2} \)
i.e., \(x+iy= \frac{u}{u^2+v^2}- i\frac{v}{u^2+v^2} \)
\( x= \frac{u}{u^2+ v^2} …(1) y= \frac{-v}{u^2+v^2} …(2) \)
The general equation is
\(a(x^2+y^2)+2gx+2fy+c=0…(3) \)
\(a[\frac{u^2}{(u^2+v^2)^2} + \frac{v^2}{(u^2+v^2)^2}]+ 2g[\frac{u}{(u^2+v^2)}]+2f[\frac{-v}{u^2+v^2}]+c=0 \)
The transformed equation is
\( c(u^2+v^2 )+ 2gu-2fv+a=0…(4) \)
(i)a≠0, c≠0→Circles not passing through the origin in z plane map onto circles not passing through the origin in the w plane.
(ii) a≠0,c=0 →Circles through the origin in z plane map onto straight line not through the origin in the w plane.
(iii) a=0,c≠0→The straight lines not through the origin in z plane map onto the circles through the origin in the w plane.
(iv) a=0,c=0 →The straight lines through the origin of z plane onto the straight lines through the origin in the w plane.

13. Which of the following is the image of the infinite series 0 <y< 1/4 under the transformation w=1/z?
a) Region outside the circle (u-1)²+v²=1
b) Region outside the circle u²+v²=1
c) Region outside the circle u²+(v+2)²=4
d) Region outside the circle u²+(v+1)²=1
View Answer

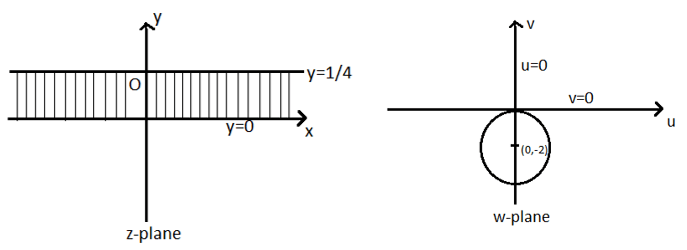
Hence, the infinite strip 0<y<1/4 is mapped into the region outside the circle u^2+〖(v+2)〗^2=4 in the lower half of the w-plane.

14. Which of the following is the image of x=3 under the transformation w=1/z?
a) \((u-\frac{1}{4})^2+v^2=(\frac{1}{4})^2 \)
b) \((u-\frac{1}{4})^2+(v-1)^2=(\frac{1}{4})^2 \)
c) \((u-\frac{1}{3})^2+v^2=(\frac{1}{4})^2 \)
d) \((u-\frac{1}{9})^2+v^2= (\frac{1}{9})^2 \)
View Answer

Answer: d
Explanation:
Given:\( w= \frac{1}{z} \)
i.e., \(z=\frac{1}{w} \)
\(z= \frac{1}{u+iv}= \frac{u-iv}{(u+iv)(u-iv)}=\frac{u-iv}{u^2+v^2} \)
\(x+iy=(\frac{u}{u^2+v^2})+ i(\frac{-v}{u^2+ v^2}) \)
i.e., \(x=(\frac{u}{u^2+ v^2})…(1), y=(\frac{-v}{u^2+v^2})…(2) \)
Given: x = 3 in the z-plane
\(3= \frac{u}{u^2+v^2} By (1) \)
\(3(u^2+v^2 )= u \)
\( u^2+v^2- \frac{1}{3} u=0 \)
\((u-\frac{1}{9})^2+v^2= (\frac{1}{9})^2 \)
It is a circle whose centre is \((\frac{1}{9}, 0)\) and radius \(\frac{1}{9} \)
x=3 in the z-plane is transformed into a circle \((u-\frac{1}{9})^2+v^2= (\frac{1}{9})^2 \) in the w plane.

15. Which of the following is the image of 1<x<3 under the mapping w= 1/z?
a) Region between the circles \((u-\frac{1}{2})^2+v^2=(\frac{1}{2})^2 and (u-\frac{1}{4})^2+v^2=(\frac{1}{4})^2 \)
b) Region between the circles \((u-\frac{1}{2})^2+v^2= 2^2 and (u-\frac{1}{3})^2+v^2= 3^2 \)
c) Region between the circles \((u-\frac{1}{2})^2+v^2= (\frac{1}{2})^2 and (u-\frac{1}{9})^2+v^2= (\frac{1}{9})^2 \)
d) Region between the circles \((u-\frac{1}{2})^2+v^2= 2^2 and (u-\frac{1}{9})^2+v^2= (\frac{1}{9})^2 \)
View Answer

Answer: c
Explanation:
Given:\( w= \frac{1}{z} \)
i.e., \(z= \frac{1}{w} \)
\(z= \frac{1}{u+iv}= \frac{u-iv}{(u+iv)(u-iv)}=\frac{u-iv}{u^2+v^2} \)
\(x+iy = (\frac{u}{u^2+v^2})+ i(\frac{-v}{u^2+ v^2}) \)
i.e., \(x=(\frac{u}{u^2+ v^2})…(1), y=(\frac{-v}{u^2+v^2})…(2) \)
Given:1 <x< 3
when x=1
\(1=\frac{u}{u^2+v^2} by (1) \)
\(u^2+v^2=u \)
\(u^2+v^2-u=0 \)
\((u-\frac{1}{2})^2+v^2= (\frac{1}{2})^2…(3) \)
It is a circle whose centre is (1/2,0) and radius is 1/2
when x=3
\(3=\frac{u}{u^2+v^2} by (1) \)
\(3(u^2+v^2)= u \)
\(u^2+v^2-\frac{u}{3}=0 \)
\((u-\frac{1}{9})^2+v^2= (\frac{1}{9})^2…(4) \)
It is a circle whose centre is (1/9,0) and radius is 1/9
Hence, the infinite strip 1 <x< 3 is transformed into the region in between the circles (3) and (4) in the w plane.

Sanfoundry Global Education & Learning Series – Complex Analysis.

To practice all areas of Complex Analysis, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Complex Analysis Questions and Answers – Evaluation of Real Integrals

» Next - Complex Mapping Questions and Answers – Transformation w = e^z

Related Posts:

Practice Numerical Methods MCQ
Apply for 1st Year Engineering Internship
Check Engineering Mathematics Books
Practice Probability and Statistics MCQ

Recommended Articles: