This set of Differential Calculus Question Bank focuses on “Derivative of Arc Length”.
1. For the cartesian curve y=f(x) with ‘s’ as arc length which of the following condition holds good?
a) \(\frac{ds}{dx} = \sqrt{1+(\frac{dy}{dx})^2}\)
b) \(\frac{d^2s}{dx^2} = \sqrt{1-(\frac{dy}{dx})^2}\)
c) \(\frac{dy}{dx} = \sqrt{1+(\frac{ds}{dx})^2}\)
d) \(\sqrt{(\frac{ds}{dx})^2 + (\frac{dy}{dx})^2} = 1\)
View Answer
Explanation: From the below figure we can notice that ds is parallel to tangent to the curve, thus ds segment make an angle of φ with x-axis in positive direction
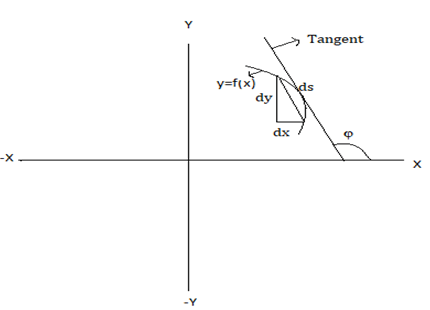
\(\frac{dy}{ds} = sinφ, \frac{dx}{ds} = cosφ, \frac{ds}{dx} = secφ, i.e (\frac{dx}{ds})^2 = sec^2 φ = 1+tan^2 φ…(1)\)
but \(tan φ=\frac{dy}{dx}\) = slope
substituting in (1) we get \( 1+(\frac{dy}{dx})^2 = (\frac{ds}{dx})^2 = \frac{ds}{dx} = \sqrt{1+(\frac{dy}{dx})^2}\).
2. For the curve \(y=a \,log \,sec(\frac{x}{a})\) what is the value of \( \frac{ds}{dx}\)? (where φ is the angle made by tangent to the curve with x-axis)?
a) cos φ
b) sec φ
c) tan φ
d) cot φ
View Answer
Explanation: w.k.t \(\frac{ds}{dx} = \sqrt{1+(\frac{dy}{dx})^2}\)
\(\frac{dy}{dx} = a \frac{tan \frac{x}{a}.sec\frac{x}{a}}{sec\frac{x}{a}} \frac{1}{a} = tan \frac{x}{a} \)
substituting we get
\(\frac{ds}{dx} = \sqrt{1+(tan \frac{x}{a})^2}=sec\frac{x}{a}, \,but \,w.k.t\, \frac{dy}{dx} = tan φ = tan\frac{x}{a} \,thus\, φ=\frac{x}{a}\)
\(\frac{ds}{dx} = secφ.\)
3. If the parametric equation of the curve is given by x=aet sint & y=aet cos t the value of \(\frac{ds}{dt}\) is given by _____
a) aet
b) 2aet
c) √3 aet
d) √2 aet
View Answer
Explanation: w.k.t \(\frac{ds}{dt} = \sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2}…(1)\)
\(\frac{dx}{dt} = ae^t (cos t + sin t), \frac{dy}{dt} = ae^t (-sin t + cost)\)
substituting in (1) we get
\(\frac{ds}{dt} = ae^t \sqrt{(cos t + sin t)^2+(-sin t+cost)^2}\)
\(\frac{ds}{dt} = ae^t \sqrt{1+2 sin t cos + 1 – 2 sin t cost} = \sqrt{2} ae^t…(cos^{2} t + sin{2} t = 1).\)
4. For the curve in polar form \(\sqrt{\frac{r}{a}} = sec(\frac{θ}{2}) \,the\, \,value\, \,of\, \frac{ds}{dθ}\) is _____
a) r sec θ
b) r sec \((\frac{θ}{2})\)
c) r sec (2θ)
d) r cosec \((\frac{θ}{2})\)
View Answer
Explanation: Squaring the given curve on both side i.e \(r=a sec ^2 (\frac{θ}{2})\)…(1)
\(\frac{dr}{dθ} = a.2 sec(\frac{θ}{2}) sec(\frac{θ}{2}) tan (\frac{θ}{2}).1/2 = a sec^2 (\frac{θ}{2}) tan(\frac{θ}{2}) \)
from (1)
\(\frac{dr}{dθ} = r tan (\frac{θ}{2}) \,the\, \,equation\, \,for\, \frac{ds}{dθ} \,is\, = \sqrt{(r^2+(\frac{dr}{dθ})^2)} = \sqrt{r^2(1+ tan^2 (\frac{θ}{2}))} \)
\(\frac{ds}{dθ} = r sec (\frac{θ}{2}).\)
5. If r=b eθ cota, where a, b are constants then ‘s’ is represented by which one of the following equation?
a) s=r sec(a)+c
b) s=r cos(a)+c
c) s=r+c
d) s=r tan(a)+c
View Answer
Explanation: r=b eθ cota
\(\frac{dr}{dθ} = b e^{θ cota}(cot a)=r cot(a) \)
w.k.t \(\frac{ds}{dr} = \sqrt{1+r^2 (\frac{dθ}{dr})^2} \,where\, \frac{dθ}{dr}=\frac{1}{r} \,tana\)
\(\frac{ds}{dr} = \sqrt{1+tan^2 a} = sec \,a \rightarrow s = \int sec \,a \,dr \, = r sec(a)+c,\) where c is constant of integration.
Sanfoundry Global Education & Learning Series – Differential Calculus.
To practice Differential Calculus Question Bank, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Engineering Mathematics Books
- Practice Numerical Methods MCQ
- Apply for 1st Year Engineering Internship
- Practice Probability and Statistics MCQ
