This set of Differential and Integral Calculus Interview Questions and Answers focuses on “Quadrature”.
1. What is meant by quadrature process in mathematics?
a) Finding area of plane curves
b) Finding volume of plane curves
c) Finding length of plane curves
d) Finding slope of plane curves
View Answer
Explanation: The process of finding area of plane curves is often called quadrature. It is an important application of integral calculus.
2. What is the formula used to find the area surrounded by the curves in the following diagram?
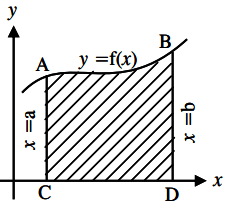
a) \(\int_a^b y \,dx\)
b) \(\int_a^b -y \,dx\)
c) \(\int_a^b x \,dy\)
d) \(\int_a^b -x \,dy\)
View Answer
Explanation: The area is present above the x-axis. Area above the x-axis is positive. The area is bounded by x-axis, curve y = f(x), straight lines x=a and x=b. Hence, area is found by integrating the curve with the lines as limits.
3. What is the formula used to find the area surrounded by the curves in the following diagram?
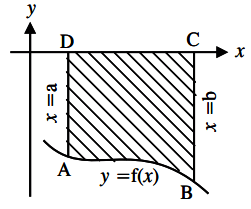
a) \(\int_a^b y \,dx\)
b) \(\int_a^b -y \,dx\)
c) \(\int_a^b x \,dy\)
d) \(\int_a^b -x \,dy\)
View Answer
Explanation: The area is present below the x-axis. Area below the x-axis is negative. The area is bounded by x-axis, curve y = f(x), straight lines x=a and x=b. Hence, area is found by integrating the curve with the lines as limits.
4. What is the formula used to find the area surrounded by the curves in the following diagram?
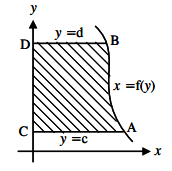
a) \(\int_c^d y \,dx\)
b) \(\int_c^d -y \,dx\)
c) \(\int_c^d x \,dy\)
d) \(\int_c^d -x \,dy\)
View Answer
Explanation: The area is present right of y-axis. Area right to y-axis is positive. The area is bounded by the y-axis, curve x = f(y), straight lines y=c and y=d. Hence, area is found by integrating the curve with the lines as limits.
5. What is the formula used to find the area surrounded by the curves in the following diagram?
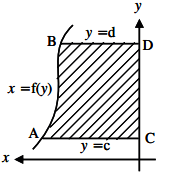
a) \(\int_c^d y \,dx\)
b) \(\int_c^d -y \,dx\)
c) \(\int_c^d x \,dy\)
d) \(\int_c^d -x \,dy\)
View Answer
Explanation: The area is present left of y-axis. Area left to y-axis is negative. The area is bounded by y-axis, curve x = f(y), straight lines y=c and y=d. Hence, area is found by integrating the curve with the lines as limits.
6. Find the area bounded in the following diagram.
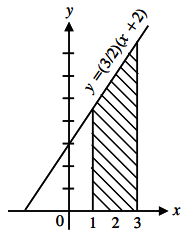
a) 6
b) 12
c) 8
d) 10
View Answer
Explanation: Area is bounded by y = \(\frac{3}{2}\) (x + 2), lines x = 1 and x = 3.
Area = \(\int_1^3 y dx = \frac{3}{2} \int_1^3 (x+2)\,dx \)
\( = \frac{3}{2} \bigg[\frac{x^2}{2} + 2x\bigg]_1^3\)
\( = \frac{3}{2} [\frac{1}{2} (9 − 1) + 2(3 − 1)] = \frac{3}{2} [4 + 4]\)
= 12 sq.units.
7. What is the area bounded by the curve y = x2 – 5x + 4, x = 2, x = 3, x-axis in the following diagram?
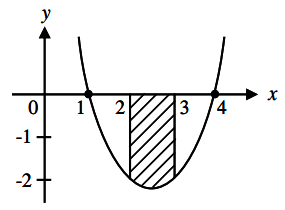
a) 13
b) 6
c) \(\frac{13}{6}\)
d) \(\frac{6}{13}\)
View Answer
Explanation: The area lies below the x-axis.
Area = ∫ -y dx
= \(\int_2^3 -(x^2-5x+4) dx\)
= \(\displaystyle\bigg[\frac{x^3}{3} – 5 \frac{x^2}{2} + 4x\bigg]_2^3\)
= \(-[(9 – (\frac{45}{2}) +12) – ((\frac{8}{3}) – (\frac{20}{2}) + 8)] \)
= \(– \left(-\frac{13}{6}\right)\)
= \(\frac{13}{6} \) sq.units.
Sanfoundry Global Education & Learning Series – Differential and Integral Calculus.
To practice all areas of Differential and Integral Calculus for Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Probability and Statistics MCQ
- Check Engineering Mathematics Books
- Apply for 1st Year Engineering Internship
- Practice Numerical Methods MCQ
