This set of Complex Analysis Multiple Choice Questions & Answers (MCQs) focuses on “Complex Conjugates”.
1. Consider two complex numbers, x and y satisfying |x|=|y| and Arg(x)+Arg(y)=π. What is x in terms of y?
a) y̅
b) -y̅
c) y
d) -y
View Answer
Explanation: Let |x|=|y|=r, therefore, x=reiα and y=reiβ, where, α+β=π,
Hence, x=rei(π-β)=reiπe-iβ
Therefore, x=-re-iβ=-y̅.
2. Let two complex numbers z and ω satisfy z > \(\overline{\omega}\). Find the value of the expression zIm(ω)+ωIm(z)+zω, if Re(z) and Re(ω) are the roots of the equation x2–5x+6.
a) 2
b) 4
c) 6
d) 8
View Answer
Explanation: Since two complex numbers with non-zero complex parts cannot be compared, therefore, Im(z) and Im(ω) are zero. Also, since z and ω are the roots of x2–5x+6, zω=6. Hence the expression equals 1+1+6=8.
3. Consider the Argand Plane shown below.
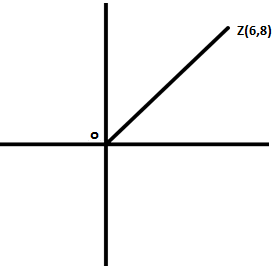
If another complex number ω=z̅+4i, then find the area of the triangle having O, z and ω as its vertices.
a) 6
b) 12
c) 24
d) 36
View Answer
Explanation: Since ω=z̅+4i and z=6+8i (from image), therefore ω=6-8i+4i=6-4i and we get a triangle having vertices (0,0), (6,8) and (6,-4) in the Argand Plane shown. Therefore, the area is (1/2)×(base)×(height)=(1/2)×(8+4)×6=36.
4. For two complex numbers p and q, if Arg(p)-Arg(q)=π/2 as well as |pq|=1, what is the value of p̅q ?
a) -i
b) -1
c) i
d) 1
View Answer
Explanation: p̅q=|p|e-iarg p×|q|eiarg q
= e-i(arg p-arg q) (since |pq|=1)
= e-iπ/2=-i.
5. What is the area of the rectangle whose vertices are the roots of the equation zz̅3+z̅z3=350, given that Re(z) and Im(z) are integers ?
a) 12
b) 24
c) 36
d) 48
View Answer
Explanation: Taking zz̅ common, we have, (z2+z̅2) zz̅=350
Hence, (x2+y2)(x2-y2)=175=25×7
∴ x2+y2=25 and x2-y2=7
Hence, x=±4, y=±3, implying, Area=8×6=48.
6. Consider the complex number z, for which a line segment A is drawn connecting origin and the point z. Also, consider the line segment B connecting origin and z̅. if z = x+iy, and the smaller angle between A and B is α, then select the incorrect option.
a) α=π/2 if x=y
b) α>π/2 if |y|>|x|
c) α=π/2 if x=-y
d) α=2×Arg(z)
View Answer
Explanation: if x=y or x=-y, |Arg(z)|=π/4 and α=2× π/4=π/2.
Now, if |y|>|x|, then |Arg(z)|>π/4 and α>2×π/4=π/2.
If z=i-1, then, Arg(z)=3π/4 but α=π/2, ∴ α≠2×Arg(z).
7. For a complex number z, if Re(z) and Im(z) are the roots of x2-7x+12=0 and z+z̅ is one of the roots of x2–10x+16=0, then, find Re(z)-Im(z).
a) 1
b) -1
c) 3
d) -3
View Answer
Explanation: Re(z) and Im(z) have values 3 and 4. Also 2Re(z) is either 2 or 8.
Merging, the two conditions, we get, Re(z)=4 and Im(z)=3.
∴ The required value is 4-3=1.
8. Let z=sinx+icos2x and ω=cosx-isin2x. Then for what values of x are z and ω conjugate of each other?
a) x = nπ
b) x = 0
c) x = (n+1/2)π
d) no value of x
View Answer
Explanation: z̅=ω
∴ sinx=cosx and cos2x=sin2x
This is not possible for any value of x.
9. If a complex number z, with integral real and imaginary parts, satisfies z2+ z̅2=16, then find the value of |z|.
a) 21/2
b) 4
c) 81/2
d) 101/2
View Answer
Explanation: Let z=x+iy, then, x2–y2=8 (by replacing z by x+iy in the given equation)
Since, x and y are integers, |x|=3 and |y|=1 are the only possible values.
Therefore, |z|=(32+12)1/2=101/2.
10. If the complex numbers (x2-3x+2)+i(y2-11y+40) and (x2-6x+8)+i(y2-9x+10) are conjugates of each other, Then what is the value of |x+iy|?
a) 131/2
b) 191/2
c) 231/2
d) 291/2
View Answer
Explanation: We have, x2-3x+2=x2-6x+8 and y2-11y+40+y2-9x+10=0
Hence, x=2, y=5
∴ |2+5i|=291/2.
11. The hyperbola, x2–y2=1 can be represented on the Argand Plane by which of the following equations?
a) z2-z̅2=1
b) z2+z̅2=1
c) z2-z̅2=2
d) z2+z̅2=2
View Answer
Explanation: Put z = x+iy. Simplifying z2-z̅2=1 gives 4xyi=1(incorrect);
Simplifying z2+z̅2=1 gives 2x2–2y2=1(incorrect);
Simplifying z2-z̅2=2, we get 2xyi=1(incorrect);
Finally, simplifying z2+z̅2=2 gives x2–y2=1(correct).
12. If z and ω are the complex conjugates of each other, then find the value of (lnz+lnω)/ln|z|.
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: lnz+lnω=ln|z|+iargz+ln|ω|+iargω
Since, |z|=|ω| and arg z+arg ω=0, ∴ lnz+lnω=2ln|z|
∴ Required value=2ln|z|/ln|z|=2.
13. Let zz̅=64, and ω\(\overline{\omega}\)=36. Find the maximum possible value of |z+ω|.
a) 8
b) 10
c) 12
d) 14
View Answer
Explanation: We know that, zz̅=64=|z|2, ∴ |z|=8, similarly, |ω|=6.
Therefore, |z+ω| ≤ |z|+|ω|=8+6=14.
14. Let z and ω be complex numbers such that ω has non-zero imaginary part and z≠1. If the expression (ω-\(\overline{\omega}\)z)/(1-z) is purely real, then find the set of values of z.
a) {z : |z|=1}
b) {z : z=z̅}
c) {z : z≠1}
d) {z : |z|=1, z≠1}
View Answer
Explanation: (ω-\(\overline{\omega}\)z)/(1-z) = (\(\overline{\omega}\)-ωz̅)/(1-z̅)⇒(zz̅-1)(\(\overline{\omega}\)-ω) = 0
⇒zz̅=1⇒|z|2=1⇒|z|=1.
15. Let z and ω be complex numbers satisfying zz̅+ω\(\overline{\omega}\)=100. If |z|,|ω|∈I, then find the minimum possible value of the expression |z+ω|.
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: zz̅+ω\(\overline{\omega}\)=100⇒|z|2+|ω|2=100, also, since |z|, |ω|∈I+, therefore, (|z|,|ω|)=(8,6) or (6,8). Hence, |z+ω|≥||z|-|ω||=|8-6|=2.
Sanfoundry Global Education & Learning Series – Complex Analysis.
To practice all areas of Complex Analysis, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Numerical Methods MCQ
- Apply for 1st Year Engineering Internship
- Check Engineering Mathematics Books
- Practice Probability and Statistics MCQ
