Class 10 Maths MCQ – Triangles

This set of Class 10 Maths Chapter 6 Multiple Choice Questions & Answers (MCQs) focuses on “Triangles”. These MCQs are created based on the latest CBSE syllabus and the NCERT curriculum, offering valuable assistance for exam preparation.

1. If the areas of two similar triangles are in the ratio 361:529. What would be the ratio of the corresponding sides?
a) 19 : 23
b) 23 : 19
c) 361 : 529
d) 15 : 23
View Answer

Answer: a
Explanation: We know that the ratio of areas of similar triangles is equal to the ratio of the squares of their corresponding sides.
Here the ratio of areas of two similar triangles is 361:529.
   
According to the theorem,
\(\frac {area \, of \, triangle \, \triangle ABC}{area \, of \, triangle \, \triangle DEF}=(\frac {AB}{DE})\)²
\(\frac {361}{529}=(\frac {AB}{DE})\)²
\(\sqrt {\frac {361}{529}}=\frac {AB}{DE}\)
\(\frac {AB}{DE}=\frac {19}{23}\)

2. What will be the value of BC if the area of two similar triangles ∆ABC and ∆PQR is 64cm² and 81cm² respectively and the length of QR is 15cm.
a) \(\frac {40}{9}\)
b) \(\frac {40}{6}\)
c) \(\frac {4}{3}\)
d) \(\frac {40}{3}\)
View Answer

Answer: d
Explanation: We know that the ratio of areas of similar triangles is equal to the ratio of the squares of their corresponding sides.
Here the area of ∆ABC is 64cm² and area of ∆PQR is 81cm². Also, QR = 15 cm
   
According to the theorem,
\(\frac {area \, of \, triangle \, \triangle ABC}{area \, of \, triangle \, \triangle PQR}=(\frac {BC}{QR})\)²
\(\frac {64}{81}=(\frac {BC}{15})\)²
\(\sqrt {\frac {64}{81}}=\frac {BC}{15}\)
\(\frac {BC}{15}=\frac {8}{9}\)
BC = \(\frac {8}{9}\) × 15 = \(\frac {4}{3}\)

3. The areas of two similar triangles are 100cm² and 64cm². If the altitude of the smaller triangle is 5.5 cm, then what will be the altitude of the corresponding bigger triangle?
a) 4.4 cm
b) 4.5 cm
c) 2.4 cm
d) 2.5 cm
View Answer

Answer: a
Explanation: We know that the ratio of areas of similar triangles is equal to the ratio of the squares of their corresponding altitudes.
Here the area of ∆ABC is 100cm² and area of ∆PQR is 64cm². Also, AD = 5.5 cm

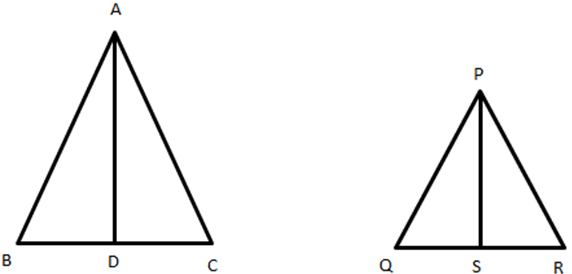
According to the theorem,
\(\frac {area \, of \, triangle \, \triangle ABC}{area \, of \, triangle \, \triangle PQR}=(\frac {AD}{PS})\)²
\(\frac {100}{64}=(\frac {5.5}{PS})\)²
\(\sqrt {\frac {100}{64}}=\frac {5.5}{PS}\)
\(\frac {5.5}{PS}=\frac {10}{8}\)
PS = \(\frac {5.5}{10} × 8 = \frac {44}{10}\) = 4.4

4. The area of two similar triangles is 25cm² and 121cm². If the median of the bigger triangle is 10 cm, then what will be the corresponding median of the smaller triangle?
a) \(\frac {51}{11}\)
b) \(\frac {10}{11}\)
c) \(\frac {50}{11}\)
d) \(\frac {5}{11}\)
View Answer

Answer: d
Explanation: We know that the ratio of areas of similar triangles is equal to the ratio of the squares of their corresponding medians.
Here the area of ∆ABC is 25cm² and area of ∆PQR is 121cm². Also, PS = 10 cm

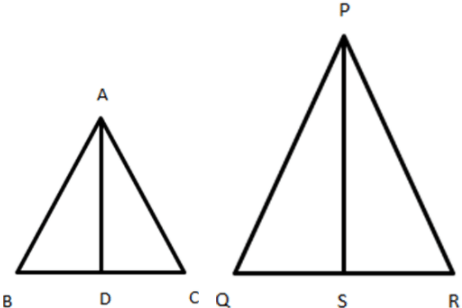
According to the theorem,
\(\frac {area \, of \, triangle \, \triangle ABC}{area \, of \, triangle \, \triangle PQR}=(\frac {AD}{PS})\)²
\(\frac {25}{121}=(\frac {AD}{10})\)²
\(\sqrt {\frac {25}{121}}=\frac {AD}{10}\)
\(\frac {AD}{10}=\frac {5}{11}\)
PS = \(\frac {5}{11} × 10 = \frac {50}{11}\)

5. ∆ABC ∼ ∆PQR, AD & PS are the angle bisectors of respectively. If AD = 1.5cm and PS = 2.3 cm then, what will be the ratio of the areas of ∆ABC and ∆PQR?
a) 19 : 15
b) 225 : 529
c) 529 : 225
d) 15 : 17
View Answer

Answer: b
Explanation: We know that the ratio of areas of similar triangles is equal to the ratio of the squares of their corresponding angle bisectors.
Here, AD=1.5 cm and PS=2.3 cm

According to the theorem,
\(\frac {area \, of \, \triangle ABC}{area \, of \, \triangle PQR}=(\frac {AD}{PS})\)²
\(\frac {area \, of \, triangle \, ABC}{area \, of \, triangle \, PQR}=(\frac {1.5}{2.3})\)²
\(\frac {area \, of \, \triangle ABC}{area \, of \, \triangle PQR}=\frac {2.25}{5.29}=\frac {225}{529}\)

6. In the given figure, DE∥BC and AE:EC=3:4. What will be the ratio of the areas ∆ADE and ∆ABC?

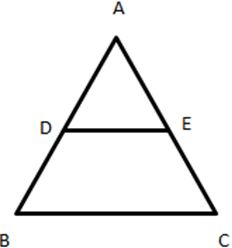
a) 16 : 9
b) 7 : 3
c) 49 : 9
d) 9 : 49
View Answer

7. In the given figure PQ∥BC, and 3AP=4PB. What will be the ratio of areas ∆ABC and trap.(PQCB)?

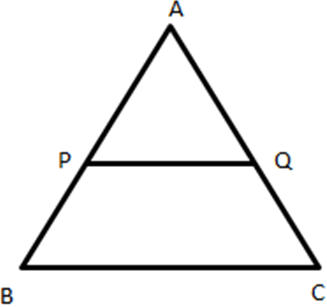
a) 9 : 7
b) 7 : 9
c) 16 : 7
d) 16 : 9
View Answer

8. In the given figure, AC is the angle bisector and AB = 5.2 cm, AD = 4.5 cm. What will be ratios of areas of ∆ABC and ∆ACD?
a) 131 : 90
b) 131 : 91
c) 121 : 81
d) 120 : 80
View Answer

Answer: c
Explanation: We know that the ratio of areas of similar triangles is equal to the ratio of the squares of their corresponding altitudes.
Here, AB=5.2cm and AD=4.5 cm

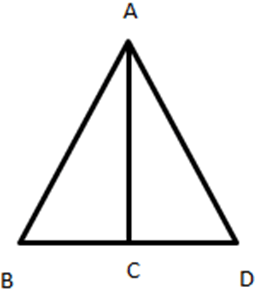
Now, In ∆ACD & ∆ACB
∠ACD = ∠ACB     (Both 90°)
AC = AC     (Common side)
∠BAC = ∠DAC     ( AC is the angle bisector)
Hence, ∆ACD ∼ ∆ACB     (By, ASA similarity test)
According to the theorem,
\(\frac {area \, of \, \triangle ABC}{area \, of \, \triangle ADC}=(\frac {AB}{AD}) \)²
\(\frac {area \, of \, \triangle ABC}{area \, of \, \triangle ADC}=(\frac {5.5}{4.5}) \)²
\(\frac {area \, of \, \triangle ABC}{area \, of \, \triangle PQR}=\frac {30.25}{20.25}=\frac {121}{81} \)

9. What will be the ratios of areas of similar ∆ABC and ∆PQR, if the altitudes of the triangles are 10cm and 5.5cm respectively?
a) 150 : 4
b) 300 : 7
c) 100 : 3
d) 400 : 9
View Answer

Answer: d
Explanation: We know that the ratio of areas of similar triangles is equal to the ratio of the squares of their corresponding altitudes.
Here, AD = 10cm and PS = 5.5 cm

According to the theorem,
\(\frac {area \, of \, \triangle ABC}{area \, of \, \triangle PQR}=(\frac {AD}{PS})\)²
\(\frac {area \, of \, \triangle ABC}{area \, of \, \triangle PQR}=(\frac {10}{5.5})\)²
\(\frac {area \, of \, \triangle ABC}{area \, of \, \triangle PQR}=\frac {100}{2.25}=\frac {400}{9}\)

10. If two triangles are similar, then the ratio of their areas will equal to ratio of the corresponding sides.
a) True
b) False
View Answer

Answer: b
Explanation: Ratio of similar triangles is equal to the square of their sides.

Since, ∆ABC ∼ ∆PQR, so they are equiangular and their sides are proportional.
∴ \(\frac {AB}{PQ}=\frac {AC}{PR}=\frac {BC}{QR}\), ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R
\( \frac {area \, of \, triange \, ABC}{area \, of \, triange \, PQR}=\frac {\frac {1}{2} \times BC \times AD}{\frac {1}{2} \times QR \times PS}=\frac {BC \times AD}{QR \times PS}\)
Now, ∆ADB and ∆PS,
∠ABD = ∠PQS
∠B = ∠Q
Hence, ∆ABC ∼ ∆PQS
So, \( \frac {AD}{PS}=\frac {AB}{PQ}\)
But, \( \frac {AB}{PQ}=\frac {BC}{QR}\)
∴ \( \frac {AD}{PS}=\frac {BC}{QR}\)
\( \frac {area \, of \, triange \, ABC}{area \, of \, triange \, PQR}=\frac {\frac {1}{2} \times BC \times AD}{\frac {1}{2} \times QR \times PS}=\frac {BC^2}{QR^2}\)

More MCQs on Class 10 Maths Chapter 6:

• Chapter 6 – Triangles MCQ (Set 2)
• Chapter 6 – Triangles MCQ (Set 3)
• Chapter 6 – Triangles MCQ (Set 4)

To practice all chapters and topics of class 10 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]