This set of Computational Fluid Dynamics online test focuses on “Energy Equation – Temperature Terms”.
1. The physical principle behind the energy equation is _____________
a) Newton’s second law of motion
b) Zeroth law of thermodynamics
c) First law of thermodynamics
d) Newton’s first law of motion
View Answer
Explanation: First law of thermodynamics is the physical principle behind the energy equation. This law states that “Energy can neither be produced nor be destroyed but can be converted from one form into another”.
2. Consider an infinitesimally small fluid element moving along with the flow. Apply the first law of thermodynamics to this model. Which of these statements is correct?
a) The rate of change of the total energy is equal to the rate of heat addition and work extraction
b) The rate of work extraction is equal to the rate of heat addition and the rate of change of the total energy
c) The rate of heat addition is equal to the rate of work extraction and the rate of change of the total energy
d) The rate of change of the total energy is equal to the rate of work extraction
View Answer
Explanation: The first law of thermodynamics applied to a system states that “The rate of change of the total energy is equal to the rate of heat addition and work extraction”.
3. The rate of heat increase in a system depends on __________
a) the rate of heat transferred to the system
b) the rate of heat generated by the system
c) neither the rate of heat generated by the system nor the rate of heat transferred to the system
d) both the rate of heat transferred to the system and the rate of heat generated by the system
View Answer
Explanation: Heat can be added to a system in two ways:
Transfer of heat across the surface of the element by surface forces.
The heat generated by the system itself.
4. To get the energy equation in terms of temperature, this law is used.
a) Newton’s third law of motion
b) Zeroth law of thermodynamics
c) Fick’s law
d) Fourier’s law of heat conduction
View Answer
Explanation: Fourier’s law of heat conduction gives the relationship between heat energy and temperature. This is used in the energy equation to convert heat terms to temperature terms.
5. The rate of change of energy in a moving model is \(\rho\frac{De}{Dt}\). In the final equation, this term is reduced to \(\frac{\partial(\rho e)}{\partial t}+\nabla.(\rho e\vec{V})\). Which of these equations is used for this reduction?
a) Equations of state
b) Stress-strain equation
c) Momentum equation
d) Continuity equation
View Answer
Explanation: Continuity equation is used as given below.
\(\rho\frac{De}{Dt}=\rho\frac{\partial e}{\partial t}+\rho\vec{V}.\nabla e \)
But,
\(\rho\frac{\partial e}{\partial t}=\frac{\partial(\rho e)}{\partial t}-e\frac{\partial \rho}{\partial t}\)
And
\(\rho\vec{V}.\nabla e=\nabla.(\rho e\vec{V})-e\nabla.(\rho \vec{V})\)
Therefore,
\(\rho\frac{De}{Dt}=\frac{\partial(\rho e)}{\partial t}-e\frac{\partial \rho}{\partial t}+\nabla.(\rho e\vec{V})-e\nabla.(\rho \vec{V})\)
\(\rho\frac{De}{Dt}=\frac{\partial(\rho e)}{\partial t}-e(\frac{\partial \rho}{\partial t}+\nabla.(\rho \vec{V}))+\nabla.(\rho e\vec{V})\)
Applying the continuity equation, \(\frac{\partial \rho}{\partial t}+\nabla.(\rho \vec{V})=0\), and hence
\(\rho\frac{De}{Dt}=\frac{\partial(\rho e)}{\partial t}+\nabla.(\rho e\vec{V})\).
6. The relationship between the rate of heat transfer per unit area \(\dot{q}_s\)=-(k∇T). Where, k is a scalar value of thermal conductivity and ∇T is the gradient of temperature. Which of these following is wrong according to the above equation?
a) Heat transfer is different in different directions
b) The rate of heat transfer depends upon the temperature gradient
c) Heat transfer is in the opposite direction of increasing temperature
d) k is the proportionality constant
View Answer
Explanation: The statement “Heat transfer is different in different directions” is wrong. k is a scalar means that the heat transfer is the same in all directions and the material is isotropic. For different heat transfers in different directions (anisotropic material), the proportionality constant should be a tensor.
7. The energy equation should be solved to get this variable of the flow.
a) Velocity
b) Temperature
c) Density
d) Pressure
View Answer
Explanation: It is a must to solve the energy equation when we want the temperature distribution of the system. The energy equation can give information about temperature.
8. Which of these terms represent the rate of heat addition to the system due to heat transfer?
a) -k gradT
b) k gradT
c) ∇.(k gradT)
d) ∇.(k gradT)
View Answer
Explanation: Rate of heat addition is
q=-k gradT
The total rate of heat added to the system is
-div(q)=∇.(k gradT).
9. Consider the following diagram.
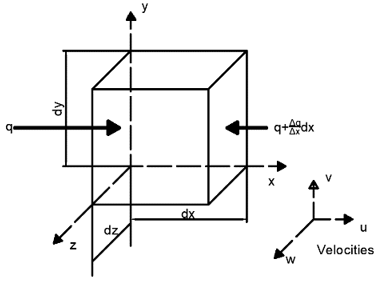
In the diagram,
q → Time rate of heat energy per unit area
q+\(\frac{\Delta q}{\Delta x}dx=q+\frac{\partial q}{\partial x}dx \)
Find the net heat transferred in x-direction.
a) –\(\frac{\partial q}{\partial x}\)
b) –\(\frac{\partial q}{\partial x}dx \,dy \,dz\)
c) –\(\frac{\partial q}{\partial x}dx\)
d) \(\frac{\partial q}{\partial x}dx \,dy \,dz\)
View Answer
Explanation:
heat transfer into the element in x-direction = q dy dz
heat transfer out of the element in x-direction = \((q+\frac{\partial q}{\partial x}dx)dy \,dz\)
net heat transfer in x-direction = q dy dz-\((q+\frac{\partial q}{\partial x}dx)dy \,dz\)
net heat transfer in x-direction = –\(\frac{\partial q}{\partial x}dx\,dy\,dz\).
10. In the general transport equation, ϕ is the flow property. To get the energy equation out of this general equation, which of these variables cannot be used?
a) v
b) T
c) h0
d) i
View Answer
Explanation: T, h0 and I represent temperature, total enthalpy and internal energy. These can be used to get the energy equation. Y-velocity component (v) cannot be used. It will result in the y-momentum equation.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics for online tests, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Chemical Engineering Books
- Practice Chemical Engineering MCQs
- Apply for Mechanical Engineering Internship
- Check Computational Fluid Dynamics Books
- Practice Mechanical Engineering MCQs
