Computational Fluid Dynamics Questions and Answers – Continuity Equation – Finite Control Volume

This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Continuity Equation – Finite Control Volume”.

1. The physical principle behind the continuity equation is __________
a) Mass conservation
b) Zeroth law of thermodynamics
c) First law of thermodynamics
d) Energy conservation
View Answer

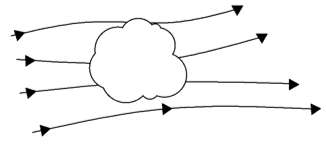
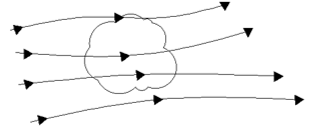
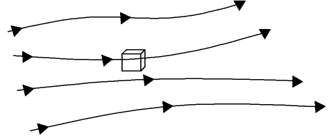
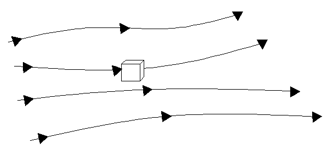
2. Which of these models directly gives this equation?
\(\frac{∂}{∂t}\iiint_v\rho dV+\iint_s \rho\vec{V}.\vec{dS}=0 \)
a)

b)

c)

d)

View Answer

3. Which of these models directly gives this equation?
\(\frac{D}{Dt}\iiint_v\rho dV = 0\)
a)

b)

c)

d)

View Answer

4. Consider a model of finite control volume (volume V and surface area S) fixed in space with elemental volume dV, vector elemental surface area d\(\vec{S}\), density ρ and flow velocity \(\vec{V}\). What is the net mass flow rate out of the surface area?
a) \(\iint_V\rho \vec{V}.dV\)
b) \(\rho \vec{V}.d \vec{S}\)
c) \(\iiint_V\rho \vec{V}.d\vec{S}\)
d) \(\iint_V\rho \vec{V}.d\vec{S}\)
View Answer

5. Consider a model of finite control volume (volume V and surface area) fixed in space with elemental volume dV, vector elemental surface area d\(\vec{S}\), density ρ and flow velocity \(\vec{V}\). What is the mass inside the control volume?
a) \(\iint_s\rho \vec{V}.d\vec{S}\)
b) \(\iiint_V\rho dV\)
c) ρdV
d) \(\frac{\partial}{\partial t} \iiint_V\rho dV\)
View Answer

6. Consider a model of finite control volume (volume V and surface area) moving along the flow with elemental volume dV, vector elemental surface area d\(\vec{S}\), density ρ and flow velocity \(\vec{V}\). What is the time rate of change of mass inside the control volume?
a) \(\iiint_V\rho dV\)
b) \(\frac{\partial}{\partial t} \iiint_V\rho dV\)
c) \(\frac{D}{Dt} \iiint_V\rho dV\)
d) ρdV
View Answer

7. To convert the non-conservative integral equation of mass conservation into the conservative integral form, which of these theorems is used?
a) Stokes theorem
b) Kelvin-Stokes theorem
c) Gauss-Siedel theorem
d) Gauss Divergence Theorem
View Answer

8. Consider a model of finite control volume (volume V and surface area) fixed in space with elemental volume dV, vector elemental surface area d\(\vec{S}\), density ρ and flow velocity \(\vec{V}\).
\(\rho\vec{V}.d\vec{S}\) is positive when _____________
a) The mass flow is outward
b) The mass flow is inward
c) The mass flow is positive
d) The mass flow is negative
View Answer

9. What is the physical statement of mass conservation equation for a finite control volume fixed in space?
a) Net mass flow through the control surface = constant
b) Rate of change of mass inside the control volume = constant
c) Net mass flow through the control surface = Rate of change of mass inside the control volume
d) Net mass flow through the control surface≠Rate of change of mass inside the control volume
View Answer

10. What is the physical statement of mass conservation equation for a finite control volume moving along with the flow?
a) Rate of change of mass inside the control volume = 0
b) Rate of change of mass inside the control volume = constant
c) Net mass flow through the control surface = Rate of change of mass inside the control volume
d) Net mass flow through the control surface≠Rate of change of mass inside the control volume
View Answer

Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.

To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]