This set of Computational Fluid Dynamics Questions and Answers for Entrance exams focuses on “FVM for Multi-dimensional Steady State Diffusion”.
1. Which of these equations represent the semi-discretized equation of a 2-D steady-state diffusion problem?
a) \(\int_A(\Gamma A\frac{\partial \phi}{\partial x})dA+\int_A(\Gamma A \frac{\partial\phi}{\partial y}) dA+\int_{\Delta V} S\,dV=0\)
b) \(\int_A\frac{\partial}{\partial x}(\Gamma A \frac{\partial\phi}{\partial x})dA+\int_A\frac{\partial}{\partial y}(\Gamma A\frac{\partial\phi}{\partial y})dA+\int_{\Delta V}S\, dV=0\)
c) \(\int_A(\Gamma A\frac{d\phi}{dx})dA+\int_A(\Gamma A \frac{d\phi}{dy})dA+\int_{\Delta V}S\, dV=0\)
d) \(\frac{\partial \phi}{\partial t}+\int_A\frac{\partial}{\partial x}(\Gamma A \frac{\partial \phi}{\partial x}) dA+\int_A\frac{\partial}{\partial y}(\Gamma A \frac{\partial \phi}{\partial y})dA+\int_{\Delta V}S\, dV=0\)
View Answer
Explanation: The general governing equation for a 2-D steady-state diffusion problem is given by
\(\frac{\partial}{\partial x}(\Gamma\frac{\partial \phi}{\partial x})+\frac{\partial}{\partial y}(\Gamma\frac{\partial \phi}{\partial y})+S=0\)
Here, partial differentiation is used as the variable φ varies in both x and y directions, but the differentiation is only in the required direction.
Integrating the equation with respect to the control volume,
\(\int_{\delta V}\frac{\partial}{\partial x}(\Gamma\frac{\partial\phi}{\partial x})dV+\int_{\delta V}\frac{\partial}{\partial y}(\Gamma\frac{\partial \phi}{\partial y})dV+\int_{\Delta V} S \,dV=0\)
Applying Gauss Divergence theorem,
\(\int_A(\Gamma A\frac{\partial\phi}{\partial x})dA+\int_A(\Gamma A\frac{\partial\phi}{\partial y})dA+\int_{\Delta V}S \,dV=0\)
This is the semi-discretized form of the equation.
2. The area in the western face of a 2-D steady-state diffusion stencil (uniform) is _______________
a) grid size in the x-direction
b) grid size in the y-direction
c) product of the grid sizes in the x and y-directions
d) ratio of the grid sizes in the x and y-directions
View Answer
Explanation: In the one-dimensional case, the area is taken to be unity. In the two-dimensional case, the area is the grid size in the perpendicular direction multiplied by unity. So, for area Ae=Aw=Δy and An=As=Δx.
3. Consider the following stencil.
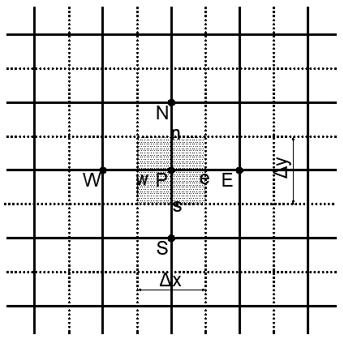
What is the flux across the northern face?
a) \(\Gamma_Na_N\frac{(\phi _N-\phi _P)}{\delta x_{PN}}\)
b) \(\Gamma_Na_N\frac{(\phi _N-\phi _P)}{\delta y_{PN}}\)
c) \(\Gamma_Na_N\frac{(\phi _E-\phi _P)}{\delta y_{PN}}\)
d) \(\Gamma_Na_N\frac{(\phi _E-\phi _P)}{\delta x_{PN}}\)
View Answer
Explanation: Flux across the northern face is \(\Gamma_N a_N\frac{\partial\phi}{\partial y}\Big|_n\). Expanding this using the central difference scheme, we get
\(\Gamma_N a_N\frac{\partial\phi}{\partial y}\Big|_n = \Gamma_Na_N \frac{(\phi _N-\phi _P)}{\delta y_PN}\).
4. Consider the following stencil.

For a source-less 2-D steady-state diffusion problem, the coefficient of the flow variable ΦP is ____
a) \(\frac{\Gamma_W A_W}{\delta x_{WP}}+\frac{\Gamma_E A_E}{\delta x_{PE}}+\frac{\Gamma_S A_S}{\delta y_SP}+\frac{\Gamma_N A_N}{\delta y_{PN}}\)
b) \(\frac{\Gamma_W A_W}{\delta y_{WP}}+\frac{\Gamma_E A_E}{\delta y_{PE}}+\frac{\Gamma_S A_S}{\delta x_SP}+\frac{\Gamma_N A_N}{\delta x_{PN}}\)
c) \(\frac{\Gamma_W A_W}{\delta y_{WP}}+\frac{\Gamma_S A_S}{\delta y_{SP}}+\frac{\Gamma_E A_E}{\delta x_{PE}}+\frac{\Gamma_N A_N}{\delta x_{PN}}\)
d) \(\frac{\Gamma_W A_W}{\delta x_{WP}}+\frac{\Gamma_S A_S}{\delta x_{SP}}+\frac{\Gamma_E A_E}{\delta y_{PE}}+\frac{\Gamma_N A_N}{\delta y_{PN}}\)
View Answer
Explanation: The general form is given by aPΦP=aEΦP+aWΦW+aNΦN+aSΦS
Here, for source-less problem, aP is the addition of all fluxes given by
\(\frac{\Gamma_W A_W}{\delta x_{WP}}+\frac{\Gamma_E A_E}{\delta x_{PE}}+\frac{\Gamma_S A_S}{\delta y_SP}+\frac{\Gamma_N A_N}{\delta y_{PN}}\).
5. If aPΦP=aEΦP+aWΦW+aNΦN+aSΦS+S is the general form of a 2-D steady-state diffusion problem, what is aE by considering the following stencil?

a) \(\frac{\Gamma_E A_E}{\delta y_{PE}}\)
b) \(\frac{\Gamma_E A_E}{\delta y_{PE}}\)
c) \(\frac{\Gamma_E A_E}{\delta x_{PE}}\)
d) \(\frac{\Gamma_E A_E}{\delta x_{WP}}\)
View Answer
Explanation: Flux in the eastern direction is given by
\(\Gamma_E A_E\frac{\partial\phi}{\partial x}\Big|_e=\Gamma_E A_E\frac{(\phi _E-\phi _P)}{\delta x_{PE}}\)
\(\Gamma_E A_E\frac{\partial\phi}{\partial x}\Big|_e=\Gamma _e A_E\frac{\phi_E}{\delta x_{PE}}-\Gamma_E a_E\frac{\phi_P}{\delta x_{PE}}\)
Expanding this while forming the general equation, we will get
\(a_E=\frac{\Gamma_E A_E}{\delta x_{PE}}\).
6. Consider the following 2-D surface with the numbers inside as the global indices of their cells.
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
The general discretized equation is of the form aPΦP=aEΦP+aWφW+aNΦN+aSΦS+S. Which of the following is correct regarding the cell numbered “13”?
a) aE=0; aW=0
b) aW=0; aN=0
c) aN=0; aS=0
d) aS=0; aW=0
View Answer
Explanation: For the control volumes adjacent to the boundary of the global domain, the boundary-side coefficient is set to zero. Therefore, for the cell numbered “13”, the southern and the western coefficients are zero (aS=0; aW=0).
7. I general, for all the steady-state diffusion problems, the discretized equation can be given as aPΦ P = ∑anbΦnb-S. For a one-dimensional problem, which of these is wrong?
a) ∑anb =aT+aB
b) ∑anb =aS+ aN
c) ∑anb =aW+aE
d) ∑anb =aP+aE
View Answer
Explanation: For a one-dimensional problem is x-direction, ∑anb =aW+aE. For a one-dimensional problem is y-direction, ∑anb =aS+ aN. For a one-dimensional problem is z-direction, ∑anb =aT+aB.
8. In a control volume adjacent to the boundary, the flux crossing the boundary is _______________ in the discretized equation.
a) set to some arbitrary constant
b) set to zero
c) introduced as a source term
d) introduced as a convective flux
View Answer
Explanation: As the boundary-side coefficients are set to zero in the discretized equations of the boundary-based control volumes, the information in the boundary may be lost. To avoid this, the flux crossing the boundary is introduced as a source term in the equation.
9. Consider a source-less 3-D steady-state diffusion problem. The general discretized equation is aP ΦP = ∑anb Φnb. What is aP?
a) aP=aW+aE+aS+aN+aT+aB
b) aP=aW+aE+aS+aN
c) aP=aW+aE+aS+aN+aT
d) aP=0
View Answer
Explanation: For all steady-state diffusion problems, in the absence of source term, aP=∑anb. Therefore, for the three-dimensional case, aP=aW+aE+aS+aN+aT+aB which includes the coefficients of all the neighbouring flow variables.
10. Consider the stencil.

The values of \(\vec{A_w}\, and\, \vec{A_s}\) are _____________
a) \(\vec{A_w}=\Delta x; \vec{A_s}=\Delta y\)
b) \(\vec{A_w}=-\Delta x; \vec{A_s}=-\Delta y\)
c) \(\vec{A_w}=-\Delta y; \vec{A_s}=-\Delta x\)
d) \(\vec{A_w}=\Delta y; \vec{A_s}=\Delta x\)
View Answer
Explanation: The values of Aw and As are Δ x and Δ y respectively. The signs of the area vectors depend on their directions. Therefore, \(\vec{A_w}=-\Delta x; \vec{A_s}=-\Delta y\).
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics for Entrance exams, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Mechanical Engineering Books
- Apply for Chemical Engineering Internship
- Practice Mechanical Engineering MCQs
- Apply for Mechanical Engineering Internship
- Check Chemical Engineering Books
