This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “High Resolution Schemes – Convection Boundedness Criterion”.
1. The numerical convection schemes should be _________
a) upwind biased
b) downwind biased
c) upwind or downwind depending on the problem
d) considering both upwind and downwind equally
View Answer
Explanation: Physically, convection transports fluid from upstream to downstream. So, the numerical convection schemes should also be upwind biased. This is why, the NVF approach involved far upwind node also but not the far downwind node.
2. According to the Godunov’s theorem, any linear monotonic scheme will be maximum ____________
a) first derivative
b) first-order accurate
c) second-order accurate
d) second derivative
View Answer
Explanation: Godunov theorem proved that any monotonic linear scheme cannot be higher-order. It will always be first order. Therefore, all the higher-order linear schemes will be non-monotonic. This is why limiters are used to construct high resolution schemes.
3. A higher-order scheme which is not of high-resolution will have ____________
a) overshoots
b) undershoots
c) undershoots and overshoots
d) damping ratio
View Answer
Explanation: The major shortcoming of the higher order schemes is the unboundedness. This can be seen in the QUICK scheme. They tend to produce undershoots or overshoots and even oscillations near the sudden jumps or steep gradients in the variable.
4. For a scheme to be bounded, its functional relationship should be ____________
a) quadratic
b) linear
c) smooth
d) continuous
View Answer
Explanation: For a scheme to be bounded, the relationship between the known and the unknown variable should be continuous. Representing in the NVF terms, the function \(\tilde{\phi_f}=f(\tilde{\phi_c})\) of a scheme should be continuous.
5. Consider the following diagram.
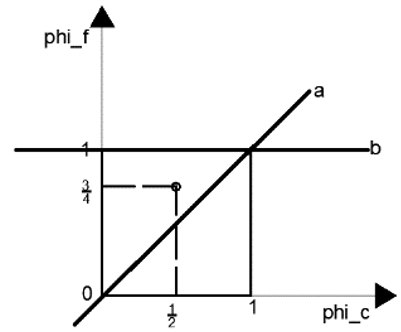
Line a in the diagram is ____________
a) compressive
b) anti-diffusive
c) diffusive
d) convective
View Answer
Explanation: Line a in the diagram represents the upwind scheme. The upwind scheme is completely diffusive. Lone b in the diagram represents downwind scheme. Downwind scheme is completely anti-diffusive or compressive.
6. Consider the following NVD.
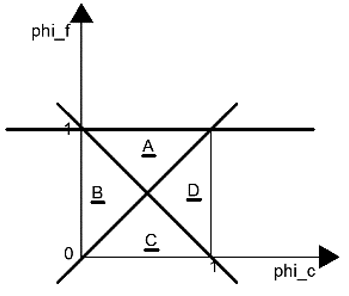
For a bounded scheme plotted in this NVD, the profile should lie inside which of these regions?
a) D, A
b) A, B
c) B, C
d) C, D
View Answer
Explanation: For a bounded scheme, the profile should lie in the region between the upwind scheme (the line connecting (0, 0) and (1, 1)) to the downwind scheme (the line connecting (0, 1) and (1, 1)) lines. This region comes under A and B.
7. In the region where \(\tilde{\phi_c}<0\, and\, \tilde{\phi_c}>1,\) a bounded scheme should have \(\tilde{\phi_f}\) as that of the ____________
(Note: \(\tilde{\phi_c} \,and\, \tilde{\phi_f}\) are the normalized flow variables at the upwind node and the face).
a) SMART scheme
b) QUICK scheme
c) Downwind scheme
d) Upwind scheme
View Answer
Explanation: One of the conditions for a scheme to be bounded is given as
\(\tilde{\phi_f}=\tilde{\phi_c}\,if \tilde{\phi_c} < 0 \,or\, \tilde{\phi_c}>1\)
This \((\tilde{\phi_f}=\tilde{\phi_c})\) resembles the function of the upwind scheme. So, we can say that the scheme should follow the upwind scheme in this region.
8. For a bounded higher-order scheme, \(\tilde{\phi_f}=1 \,when\, \tilde{\phi_c}\)= ____________
(Note: \(\tilde{\phi_c} \,and\, \tilde{\phi_f}\) are the normalized flow variables at the upwind node and the face).
a) ∞
b) 0
c) 1
d) 0.5
View Answer
Explanation: A bounded higher-order scheme should pass through the points (0, 0) and (1, 1) in the NVD. So, at \(\tilde{\phi_c}=1,\) the value of \(\tilde{\phi_f}\) should also be 1. Similarly, when \(\tilde{\phi_c}=0, \, \tilde{\phi_f}=0.\)
9. In the region where \(\tilde{\phi_c}<0 \,and\, \tilde{\phi_c}>1,\) ___________ is dominant.
(Note: \(\tilde{\phi_c} \,and\, \tilde{\phi_f}\) are the normalized flow variables at the upwind node and the face).
a) conduction
b) convection
c) radiation
d) anti-diffusion
View Answer
Explanation: In this region, convection is high. This is why, the solution follows the upwind scheme. When convection is dominant, the scheme should be upwind biased as the process is from the upstream to downstream.
10. Consider the diagrams. They give the NVD. The thick line represents the scheme. Which of these schemes is unbounded?
a) 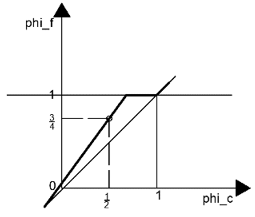
b) 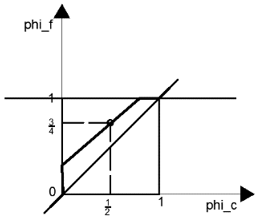
c) 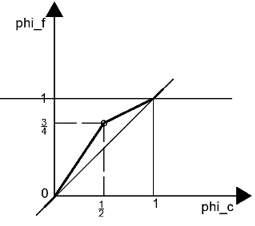
d) 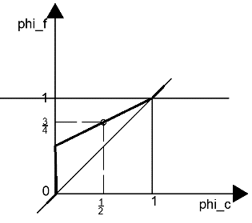
View Answer
Explanation: For a scheme to be bounded, it should pass through the point (0, 0). This means that at \(\tilde{\phi_c}=0, \tilde{\phi_f}=0.\) But, in the diagram (refer below), the profile of the scheme does not pass through the point (0, 0). So, the scheme is unbounded.

Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Mechanical Engineering Books
- Check Chemical Engineering Books
- Practice Chemical Engineering MCQs
- Practice Mechanical Engineering MCQs
- Check Computational Fluid Dynamics Books
