This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Discretization Aspects – Grid Generation”.
1. Which of these analyses needs a stretched grid?
a) Transient flow over a flat plate
b) Incompressible flow over a flat plate
c) Viscous flow over a flat plate
d) Subsonic flow over a flat plate
View Answer
Explanation: A stretched grid has less grid spacing in one side of the domain and stretched in the other side. For viscous flow over a flat plate, the boundary layer will have much variations of the flow properties than the far regions. So, for modelling this, stretched grids can be used.
2. Let x, y be the coordinates in the physical domain and ξ, η be the coordinates in the computational domain. In which of these cases, the horizontal lines are stretched and the vertical lines are equally spaced?
a) ξ=x; η=ln(y+1)
b) ξ=ln(x+1); η=y
c) ξ=x; η=y
d) ξ=ln(x+1); η=ln(y+1)
View Answer
Explanation: The horizontal coordinate lines are stretched means that the grids are stretched in the y-direction. Coordinates are stretched when logarithmically spaced. So, to get vertically stretched grid, η=ln(y+1). Horizontal coordinates are undisturbed.
3. Form the continuity equation for steady 2-dimensional flow when the x-direction grids are stretched.
Density → ρ
x and y-velocities → u,v
Coordinates in physical domain → x,y
Coordinates in computational domain → ξ, η.
a) \(e^\eta\frac{\partial(\rho u)}{\partial\xi}+\frac{\partial(\rho v)}{\partial\eta}\)
b) \(\frac{\partial(\rho u)}{\partial\xi}+e^\xi\frac{\partial(\rho v)}{\partial\eta}\)
c) \(\frac{\partial(\rho u)}{\partial\xi}+e^\eta\frac{\partial(\rho v)}{\partial\eta}\)
d) \(e^\xi\frac{\partial(\rho u)}{\partial\xi}+\frac{\partial(\rho v)}{\partial\eta}\)
View Answer
Explanation: The continuity equation for steady 2-dimensional flow is:
\(\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}=0\)
For stretched coordinates in the x-direction,
ξ = ln(x+1) ⇒ x = eξ-1 ⇒∂x = eξ∂ξ
η = y ⇒ y = η ⇒ ∂y = ∂η
Converting the continuity equation to computational domain terms,
\(\frac{\partial(\rho u)}{\partial\xi}\frac{\partial\xi}{\partial x} + \frac{\partial(\rho u)}{\partial \eta} \frac{\partial\eta}{\partial x} + \frac{\partial(\rho v)}{\partial\xi}\frac{\partial\xi}{\partial y}+\frac{\partial(\rho v)}{\partial\eta}\frac{\partial \eta}{\partial y}=0\)
\(\frac{\partial(\rho u)}{\partial\xi}\frac{1}{e^\xi} + \frac{\partial(\rho v)}{\partial \eta}1=0\)
\(\frac{\partial(\rho u)}{\partial\xi} + e^ξ\frac{\partial(\rho v)}{\partial \eta} =0\).
4. Consider a divergent nozzle as shown in the figure.
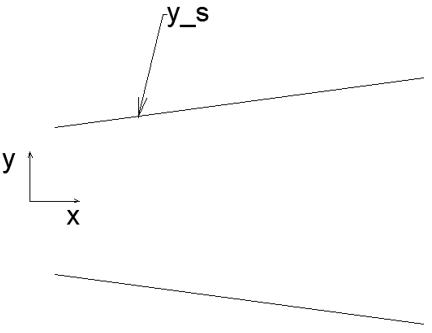
Let x, y be the coordinates in the physical domain and ξ, η be the coordinates in the computational domain. Which of these equations can give the best-suited grid for this system?
a) ξ=x; η = y×ys
b) ξ=x×ys; η=y×ys
c) \(\xi=\frac{x}{y_s};\eta=\frac{y}{y_s}\)
d) \(\xi=x;\eta=\frac{y}{y_s}\)
View Answer
Explanation: The given divergent nozzle needs a boundary-fitted grid to suit its divergent nature. The variation exists only in the y-direction. The x-directions grids can be uniformly spaced. So, the best-suited coordinates are \(\xi=x;\eta=\frac{y}{y_s}\).
5. Adaptive grids change automatically based on ______________
a) flow field gradients
b) time rate of change of the flow properties
c) grid gradients
d) time rate of change of the grid points
View Answer
Explanation: Adaptive grids are the one which can automatically adapt their arrangement based on the needs of the problem. This is based on the flow-field gradients. High flow-field gradients indicate a sudden variation of properties based on spatial coordinates. So, more grids are automatically generated there.
6. Let x, y be the coordinates in the physical domain and ξ, η be the coordinates in the computational domain. Which of these is correct for adaptive grids?
a) \(\frac{\partial\xi}{\partial x}≠1 \)
b) \(\frac{\partial\xi}{\partial x}≠0 \)
c) \(\frac{\partial\xi}{\partial t}≠0 \)
d) \(\frac{\partial\xi}{\partial t}≠1 \)
View Answer
Explanation: Adaptive grids change with varying time. So, the time rate of change of coordinates will never be equal to zero. This is given by\(\frac{\partial\xi}{\partial x}≠0 \). They may or may not vary from the physical coordinates.
7. Which of these properties are balanced by using adaptive grids?
a) Accuracy and convergence
b) Efficiency and stability
c) Accuracy and stability
d) Accuracy and efficiency
View Answer
Explanation: By automatically generating the grid points, the places without much variation are given fewer grids and the places with high variation are given more grids. This helps in maintaining a balance between efficiency of the solution and accuracy of the answers.
8. What does elliptic grid generation mean?
a) Grids generated for elliptic equations
b) Grids transformed with elliptic equations
c) The computational domain is elliptic
d) The object under consideration is elliptic
View Answer
Explanation: The one-to-one transformation of the coordinates in the physical domain to the coordinates in the computational domain is done using elliptic equations. It has nothing to do with elliptic nature of the governing equations.
9. What are zonal grids?
a) Grids generated for a particular zone of the domain of interest
b) Grids varying at different zones
c) Grids generated for a particular time in the flow
d) Grids varying with time
View Answer
Explanation: While dealing with a complex problem, grids are generated separately for different zones which are called zonal grids. These are then attached together to form grids for the whole domain.
10. Which type of grids is the best for flow over an airfoil?
a) Stretched grids
b) Adaptive grids
c) Boundary-fitted grids
d) Elliptic grids
View Answer
Explanation: The shape of the airfoil is complex. So, generating a grid that fits the boundary of this airfoil is best. Stretched grids are for flat surfaces. Adaptive grids are needed if the flow gradients are not known to the user. Elliptic grids are useful when the transformation is elliptic.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Chemical Engineering MCQs
- Check Chemical Engineering Books
- Practice Mechanical Engineering MCQs
- Apply for Mechanical Engineering Internship
- Check Mechanical Engineering Books
