This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Mathematical Behaviour of PDE – Elliptic Equations”.
1. The characteristic curves for an elliptic system are ___________
a) real and imaginary
b) both real
c) both imaginary
d) both zeros
View Answer
Explanation: Elliptic equations have their determinant less than zero and the roots of this determinant are both imaginary. So, the curves are also imaginary.
2. Under which condition does the inviscid steady flow become elliptic?
a) M=1
b) M<1
c) M>1
d) M>5
View Answer
Explanation: An inviscid steady flow is elliptic when the flow is subsonic. When the flow becomes supersonic, it changes its behaviour. Hence, it comes under the elliptic category when M<1.
3. Which of these are correct for an elliptic equation?
a) There is no limited region of influence or domain of dependence
b) There is no region of influence or domain of dependence
c) There is no region of influence, but there exists a domain of dependence
d) There is no domain of dependence, but there exists a region of influence
View Answer
Explanation: For elliptic equations, the information is spread everywhere in all directions. They have an infinite region of influence or a limited domain of dependence for these equations. But, it cannot be stated that they do not have a region of influence or domain of dependence.
4. The solution of elliptic equations depends on ___________
a) one of its boundaries
b) all its boundaries
c) its opposite boundaries
d) its adjacent boundaries
View Answer
Explanation: Any point inside the region of elliptic equations is influenced by the whole closed boundary. So, its solution depends on all of its boundaries.
5. Which of these statements is true for elliptic equations?
a) The solution can be approximated in some of the points
b) The solution can be marched from some initial conditions
c) The solution at all points must be carried out simultaneously
d) The solution process should be carried out simultaneously for some region and then marching can be done
View Answer
Explanation: Any change at any point in the domain of elliptic equation influences all other points. So, the solution process should be carried out simultaneously and it cannot be marched.
6. The solution technique used to solve elliptic equations should ___________
a) allow each point to be influenced by its boundary-side neighbours
b) allow each point to be influenced by its west neighbour
c) allow each point to be influenced by its east neighbour
d) allow each point to be influenced by all its neighbours
View Answer
Explanation: The solution technique of any problem should depend upon the type of the problem. Elliptic problems are influenced by all points in its domain. So, the solution technique should also allow all of its neighbours to influence each point.
7. Which of these flows is mathematically elliptic?
a) Transient viscous flow
b) Steady viscous flow
c) Steady inviscid flow
d) Transient inviscid flow
View Answer
Explanation: Steady viscous flow exhibits elliptic behaviour. Steady inviscid flow behaves elliptic optionally. Transient flows are not elliptic.
8. Which of these is the prototype elliptic equation?
a) Incompressible irrotational flow
b) Incompressible rotational flow
c) Compressible irrotational flow
d) Compressible rotational flow
View Answer
Explanation: The prototype elliptic equation is Laplace’s equation. This represents an incompressible irrotational fluid flow.
9. Which is an elliptic equation?
a) Wave equation
b) Transient heat conduction
c) Transient heat convection
d) Steady state heat conduction
View Answer
Explanation: Transient problems and wave equations need marching solutions and cannot be elliptic. Steady state heat conduction is elliptic.
10. The below diagram represents elliptic equations.
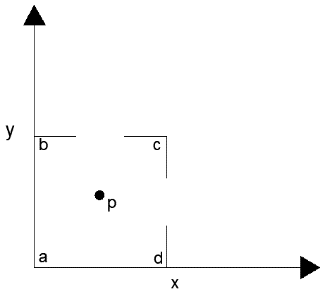
The point ‘p’ is influenced by ___________
a) ab and bc
b) ab and cd
c) closed boundary abcd
d) ab
View Answer
Explanation: The whole closed boundary influences the point ‘p’ along with its domain for elliptic equations. Thus ‘p’ is influenced by the closed boundary abcd.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Computational Fluid Dynamics Books
- Apply for Mechanical Engineering Internship
- Check Mechanical Engineering Books
- Practice Chemical Engineering MCQs
- Apply for Chemical Engineering Internship
