This set of Computational Fluid Dynamics Interview Questions and Answers focuses on “Classification of PDE – 2”.
1. What are the two methods used to find the type of PDEs?
a) Lagrangian Method and Eulerian method
b) Cramer’s method and Eulerian method
c) Cramer’s method and Lagrangian Method
d) Cramer’s method and Eigenvalue method
View Answer
Explanation: Partial differential equations can be classified using their characteristic lines. These are located using either the Cramer’s method or the Eigenvalue method.
2. Let u be a variable dependent on x and y. In the diagram, \(\frac{du}{dy}\, represents\, \frac{\partial u}{\partial y}\).
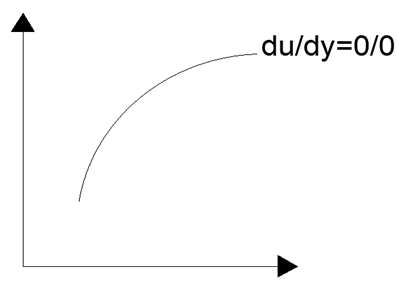
What does this line in the diagram represent?
a) Characteristic line
b) Eigenvalue line
c) Lagrange line
d) Cramer line
View Answer
Explanation: Characteristic lines are those where the derivatives of the dependent variable are indeterminate. In the diagram, (du/dy) is indeterminate and hence the line represents a characteristic line.
3. How the type of PDE is identified using Cramer’s rule?
a) By equating the Cramer’s denominator to 1
b) By equating the Cramer’s numerator to 1
c) By equating the Cramer’s denominator to 0
d) By equating the Cramer’s numerator to 0
View Answer
Explanation: The denominator of Cramer’s solution is equated to zero to find the type of PDE. The denominator is equated to zero to make the solution indeterminate.
4. What are the Cramer’s solutions equated to while using Cramer’s method of classifying a PDE?
a) The dependent variables
b) The derivatives of dependent variables
c) The second derivatives of dependent variables
d) The highest derivatives of dependent variables
View Answer
Explanation: For characteristic lines, the derivatives of dependent variables are zero. Cramer’s rule is used to find these derivatives and then it is made indeterminate to find the type of PDE.
5. _________ of the characteristic curves is used to find the type of PDE.
a) Starting point
b) Centre
c) Length
d) Slope
View Answer
Explanation: The nature of the slope of the characteristic curves gives the nature of the characteristic curves. This directly matches with the type of the PDE too.
6. What is the Cramer’s numerator when the solution is the derivative of dependent variables?
a) any negative value
b) any positive value
c) 1
d) 0
View Answer
Explanation: The solution should be indeterminate. Therefore, if the denominator is 0, the numerator must also be zero. (0/0=indeterminate).
7. Consider the following system of PDEs.
\(a_1\frac{\partial u}{\partial x}+b_1\frac{\partial u}{\partial y}+c_1\frac{\partial v}{\partial x}+d_1\frac{\partial v}{\partial y}=0\)
\(a_2\frac{\partial u}{\partial x}+b_2\frac{\partial u}{\partial y}+c_2\frac{\partial v}{\partial x}+d_2\frac{\partial v}{\partial y}=0\)
The Eigenvalues of which of these matrices can be used to classify this system of PDEs?
a) \(\begin{bmatrix}
a_1 & b_1 \\
a_2 & b_2
\end{bmatrix}^{-1}\)
\(\begin{bmatrix}
c_1 & d_1 \\
c_2 & d_2
\end{bmatrix}\)
b) \(\begin{bmatrix}
a_1 & c_1 \\
a_2 & c_2
\end{bmatrix}^{-1}\)
\(\begin{bmatrix}
b_1 & d_1 \\
b_2 & d_2
\end{bmatrix}\)
c) \(\begin{bmatrix}
a_1 & c_1 \\
a_2 & c_2
\end{bmatrix}\)
\(\begin{bmatrix}
b_1 & d_1 \\
b_2 & d_2
\end{bmatrix}\)
d) \(\begin{bmatrix}
a_1 & b_1 \\
a_2 & b_2
\end{bmatrix}\)
\(\begin{bmatrix}
c_1 & d_1 \\
c_2 & d_2
\end{bmatrix}\)
View Answer
Explanation: From the given system of PDEs,
\(a_1\frac{\partial u}{\partial x}+b_1\frac{\partial u}{\partial y}+c_1\frac{\partial v}{\partial x}+d_1\frac{\partial v}{\partial y}=0\)
\(a_2\frac{\partial u}{\partial x}+b_2\frac{\partial u}{\partial y}+c_2\frac{\partial v}{\partial x}+d_2\frac{\partial v}{\partial y}=0\)
Let, \(W=\begin{bmatrix}
u \\
v
\end{bmatrix}\) then
\(\begin{bmatrix}
a_1 & c_1 \\
a_2 & c_2
\end{bmatrix}
\frac{\partial W}{\partial x}+
\begin{bmatrix}
b_1 & d_1 \\
b_2 & d_2
\end{bmatrix}
\frac{\partial W}{\partial y}=0 \)
\(\frac{\partial W}{\partial x}+
\begin{bmatrix}
a_1 & c_1 \\
a_2 & c_2
\end{bmatrix}^{-1}
\begin{bmatrix}
b_1 & d_1 \\
b_2 & d_2
\end{bmatrix} \frac{\partial W}{\partial y}=0\)
The Eigenvalues of \(\begin{bmatrix}
a_1 & c_1 \\
a_2 & c_2
\end{bmatrix}^{-1}\) \(\begin{bmatrix}
b_1 & d_1 \\
b_2 & d_2
\end{bmatrix}\) determines the class of PDE.
8. The Eigenvalues in the Eigenvalue method are ____________
a) the type of the characteristic lines
b) the type of PDE
c) the slope of the characteristic lines
d) the slope of PDE
View Answer
Explanation: The Eigenvalues will give you the slope of the characteristic lines. Using this slope, we determine the type of the characteristic line and the type of PDE.
9. When the Eigenvalues are a mixture of real and imaginary values, the PDE is ___________
a) elliptic-hyperbolic
b) parabolic
c) elliptic
d) hyperbolic
View Answer
Explanation: When we get a mixed type of Eigenvalues, the type of PDE is also mixed. Many practical equations have mixed behaviour also.
10. Solutions of a system of PDEs can be obtained by equating the numerator of Cramer’s solution while using Cramer’s rule. This method is used by __________
a) Integral transform
b) Change of variables
c) Separation of variables
d) Method of characteristics
View Answer
Explanation: The Cramer’s numerator is equated to zero and compatibility equations are obtained. These are then solved to get the solution of PDEs.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics for Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Computational Fluid Dynamics Books
- Check Chemical Engineering Books
- Apply for Mechanical Engineering Internship
- Practice Mechanical Engineering MCQs
- Apply for Chemical Engineering Internship
