This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Finite Difference Method”.
1. The truncation error in a finite difference expansion is \(-(\frac{\partial^2 u}{\partial x^2})_{i,j} \frac{\Delta x}{2}-(\frac{\partial^3 u}{\partial x^3})_{i,j} \frac{(\Delta x)^3}{6}\). What is the order of accuracy of the finite difference equation?
a) 1
b) 2
c) -2
d) -1
View Answer
Explanation: The lowest order term in the truncation error given is \(\frac{\Delta x}{2}\), which is of the order 1. This defines the order of accuracy of the equation. So, the order of accuracy here is 1.
2. Consider the equation \((\frac{\partial u}{\partial y})_{i,j}=(\frac{u_{i,j}-u_{i,j-1}}{\Delta y})\) formulated using the Taylor series expansion. Find the type of equation.
a) first-order forward difference
b) first-order rearward difference
c) second-order forward difference
d) second-order rearward difference
View Answer
Explanation: The equation uses the terms ui,j and its rearward term ui,j-1. So, it represents a rearward difference. The order of accuracy of the equation depends on its truncation error. The truncation error has the least order term \(\frac{-\Delta y}{2}\). So, it is first order accurate.
3. Find the second-order accurate finite difference approximation of the first derivative of the velocity component (u) in the x-direction using the Taylor series expansion. (Note: i and j are in the x and y-direction respectively).
a) \(\frac{u_{i,j+1}-u_{i,j-1}}{\Delta x}\)
b) \(\frac{u_{i+1,j}-u_{i-1,j}}{\Delta x}\)
c) \(\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}\)
d) \(\frac{u_{i,j+1}-u_{i,j-1}}{2\Delta x}\)
View Answer
Explanation: The only second-order accurate finite difference approximation of the first derivative is the central difference. For getting the central difference term,
\(u_{i+1,j}=u_{i,j}+(\frac{\partial u}{\partial x})_{i,j}\Delta x+(\frac{\partial ^2 u}{\partial x^2})_{i,j}\frac{(\Delta x)^2}{2}+⋯\)
\(u_{i-1,j}=u_{i,j}-(\frac{\partial u}{\partial x})_{i,j}\Delta x+(\frac{\partial ^2 u}{\partial x^2})_{i,j}\frac{(\Delta x)^2}{2}+⋯\)
To get \((\frac{\partial u}{\partial x})_{i,j^,}\)
\(u_{i+1,j}-u_{i-1,j}=2(\frac{\partial u}{\partial x})_{i,j} \Delta x+⋯\)
\((\frac{\partial u}{\partial x})_{i,j}=\frac{u_{i+1,j}-u_{i-1,j}}{2 \Delta x}\) .
4. Find the first-order forward difference approximation of \((\frac{\partial u}{\partial x})_{i,j}\) using the Taylor series expansion.
a) \(\frac{u_{i,j+1}-u_{i,j}}{2 \Delta x}\)
b) \(\frac{u_{i+1,j}-u_{i,j}}{2 \Delta x}\)
c) \(\frac{u_{i,j+1}-u_{i,j}}{\Delta x}\)
d) \(\frac{u_{i+1,j}-u_{i,j}}{\Delta x}\)
View Answer
Explanation: To get the first-order forward difference approximation,
The Taylor series expansion of ui+1,j is
\(u_{i+1,j}=u_{i,j}+(\frac{\partial u}{\partial x})_{i,j}\Delta x+(\frac{\partial ^2 u}{\partial x^2})_{i,j}\frac{(\Delta x)^2}{2}+⋯\)
\((\frac{\partial u}{\partial x})_{i,j}=\frac{u_{i+1,j}-u_{i,j}}{\Delta x}\).
5. Using the Taylor series expansion, What is the first term of the truncation error of the finite difference equation \((\frac{\partial u}{\partial x})_{i,j}=\frac{u_{i+1,j}-u_{i,j}}{\Delta y}\)?
a) \(-(\frac{\partial^2 u}{\partial x^2})_{i,j}\frac{\Delta x}{2}\)
b) \((\frac{\partial^2 u}{\partial x^2})_{i,j}\frac{\Delta x}{3}\)
c) \(-(\frac{\partial^2 u}{\partial x^2})_{i,j}\frac{\Delta x}{3}\)
d) \((\frac{\partial^2 u}{\partial x^2})_{i,j}\frac{\Delta x}{2}\)
View Answer
Explanation: The Taylor series expansion of ui+1,j is
\(u_{i+1,j}=u_{i,j}+(\frac{\partial u}{\partial x})_{i,j} \Delta x+(\frac{\partial ^2 u}{\partial x^2})_{i,j} \frac{(\Delta x)^2}{2}+⋯\)
\(\frac{u_{i+1,j}-u_{i,j}}{\Delta x}=(\frac{\partial u}{\partial x})_{i,j}+(\frac{\partial^2 u}{\partial x^2})_{i,j}\frac{\Delta x}{2}+⋯\)
\((\frac{\partial u}{\partial x})_{i,j}=\frac{u_{i+1,j}-u_{i,j}}{\Delta x}-(\frac{\partial^2 u}{\partial x^2})_{i,j}\frac{\Delta x}{2}-…\)
The term –\((\frac{\partial^2 u}{\partial x^2})_{i,j}\frac{\Delta x}{2}-… \)is truncated. So, the first term of truncation error is –\((\frac{\partial^2 u}{\partial x^2})_{i,j}\frac{\Delta x}{2}\).
6. Find the central second difference of u in y-direction using the Taylor series expansion.
a) \(\frac{u_{i,j+1}+2u_{i,j}+u_{i,j-1}}{(\Delta y)^2}\)
b) \(\frac{u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{(\Delta y)^2}\)
c) \(\frac{u_{i,j+1}-2u_{i,j}-u_{i,j-1}}{(\Delta y)^2}\)
d) \(\frac{u_{i,j+1}+2u_{i,j}-u_{i,j-1}}{(\Delta y)^2}\)
View Answer
Explanation: To get the second difference,
\(u_{i,j+1}+u_{i,j-1}=2 u_{i,j}+(\frac{\partial^2 u}{\partial y^2})_{i,j}(\Delta y)^2+⋯\)
\((\frac{\partial^2 u}{\partial y^2})_{i,j}=\frac{u_{i,j+1}-2 u_{i,j}+u_{i,j-1}}{(\Delta y)^2} +⋯\)
After truncating,
\((\frac{\partial^2 u}{\partial y^2})_{i,j}=\frac{u_{i,j+1}-2 u_{i,j}+u_{i,j-1}}{(\Delta y)^2}\).
7. What is the order of the central difference for the mixed derivative \(\frac{\partial^2 u}{\partial x\partial y}\) while approximated using the Taylor series expansion?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: The first term in the truncation error of the central difference for the mixed derivative \(\frac{\partial^2 u}{\partial x\partial y} \,is\, -(\frac{\partial^4 u}{\partial x^3 \partial y})\frac{(\Delta x)^2}{12}\). So, the order of accuracy is 2.
8. Find \(\frac{\partial u}{\partial r}\) at point 1 using forward difference method.

a) 1000
b) 100
c) 500
d) 5000
View Answer
Explanation: Using the forward difference method,
\(\frac{\partial u}{\partial r}=\frac{u_2-u_1}{\Delta r}=\frac{5-0}{0.5×10^{-2}}=\frac{5}{5×10^{-3}}=1000.\)
9. What is the least order of accuracy for the second derivatives?
a) first-order
b) third-order
c) fourth-order
d) second-order
View Answer
Explanation: The least possible order of accuracy for the second derivatives is 2. There cannot be a first-order second derivative as the second derivatives need terms less than the second order for the approximation.
10. Order of accuracy m means _____________
a) as the grid size is reduced, the approximations converge to the exact solution with an error proportional to m powers of the grid size
b) as the grid size is reduced, the approximations converge to the exact solution with an error proportional to m times of the grid size
c) as the grid size is reduced, the approximations diverge from the exact solution with an error proportional to m powers of the grid size
d) as the grid size is reduced, the approximations diverge from the exact solution with an error proportional to m times of the grid size
View Answer
Explanation: An order of accuracy m means that the truncation error starts with a term proportional to grid sizem. So, the statement “as the grid size is reduced, the approximations converge to the exact solution with an error proportional to m powers of the grid size” is correct.
11. Which of these diagrams represent the central difference approximation of \(\frac{\partial u}{\partial x}\)?
a)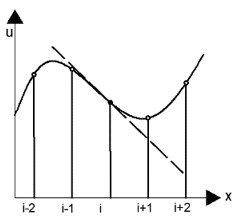
b) 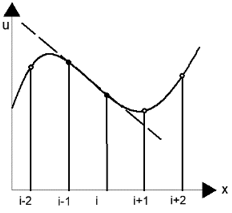
c) 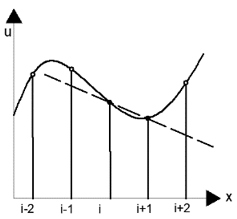
d) 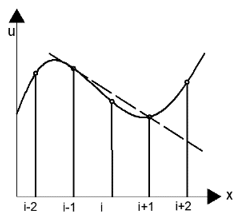
View Answer
Explanation: The line connecting the previous and the next node represents the central difference. The line connecting the previous and the current node represents the rearward difference. The line connecting the current and the next node represents the forward difference. The tangent to the curve at the point ‘i’ is the exact solution.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Chemical Engineering Books
- Practice Chemical Engineering MCQs
- Check Computational Fluid Dynamics Books
- Apply for Mechanical Engineering Internship
- Check Mechanical Engineering Books
