This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Governing Equations – Flow Models”.
1. What does this diagram represent?
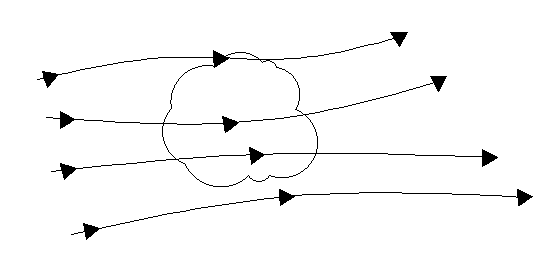
a) Finite control volume moving along with the flow
b) Stationary finite control volume
c) Infinitesimally small element with the fluid passing through it
d) Infinitesimally small element moving along with the flow
View Answer
Explanation: The diagram represents a finite control volume stationary in position. Fluid flows into and out of this model.
2. A control volume based model gives ___________ equation.
a) Integral
b) Differential
c) Conservative
d) Non-conservative
View Answer
Explanation: Control volumes are big enough that the flow properties can be integrated along it. Thus, a control volume yields an integral equation.
3. What is the need of constructing a model for analysing fluids?
a) Fluids are not stationary but they have the same velocity in different parts
b) Fluids are stationary and they have the same velocity in different parts
c) Fluids are not stationary and they have different velocities in different parts
d) Fluids are not stationary but they have the same velocity in different parts
View Answer
Explanation: A solid body can be easily divided into different parts. A fluid is squishy and it has different velocities in different parts. This creates the need for a model to analyse it.
4. If this model is used to get the governing equations, what type of equation will be obtained?
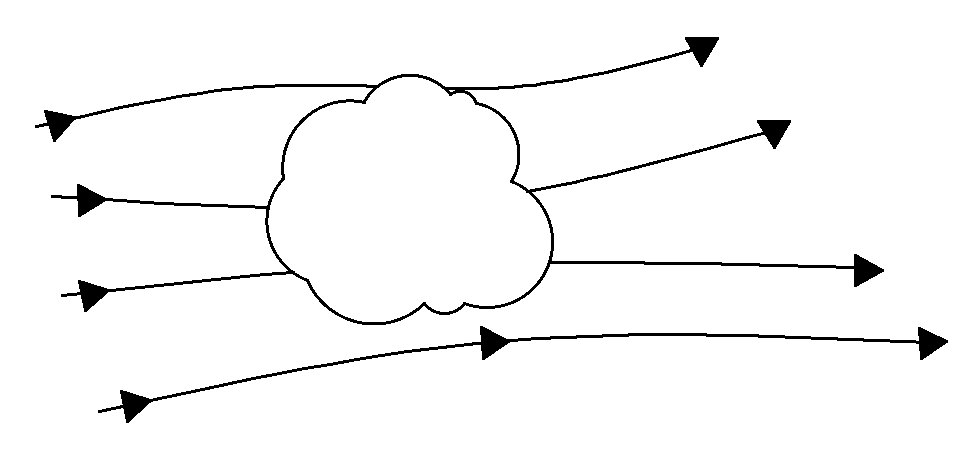
a) Non-conservative differential
b) Conservative differential
c) Conservative integral
d) Non-conservative integral
View Answer
Explanation: The given diagram represents a finite control volume moving along with the flow. This will give a non-conservative integral equation.
5. An equation modelled using infinitesimally small element leads to ____________
a) Partial differential equation
b) Integral equation
c) Differential equation
d) Linear differential equation
View Answer
Explanation: Infinitesimally small element models directly leads to a partial differential equation. The element is infinitesimal in the sense of differential calculus.
6. A finite control volume moving along with the flow __________
a) Has its position coordinates stationary
b) Has its particles moving into and out of it
c) Has the properties differentiated
d) Has the same particles always inside it
View Answer
Explanation: As the finite control volume moves along with the flow, the same particles are always concerned. The mass inside this model also does not change.
7. If this model is used to get the governing equations, what type of equation will be obtained?
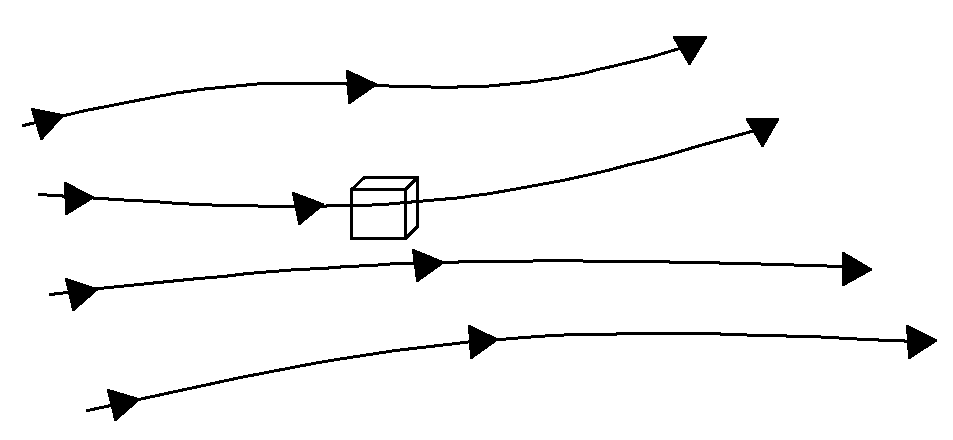
a) Non-conservative differential
b) Conservative differential
c) Conservative integral
d) Non-conservative integral
View Answer
Explanation: The given diagram represents an infinitesimally small element with the flow moving past it. This will give a conservative differential equation.
8. Other than finite control volume and infinitesimal small element, what is the third possible modelling of fluid flow?
a) Discrete approach
b) Quantum approach
c) Microscopic approach
d) Macroscopic approaches
View Answer
Explanation: A microscopic approach is possible where the laws of nature are applied to the atoms and molecules. This is regarding kinetic theory.
9. What does this diagram represent?
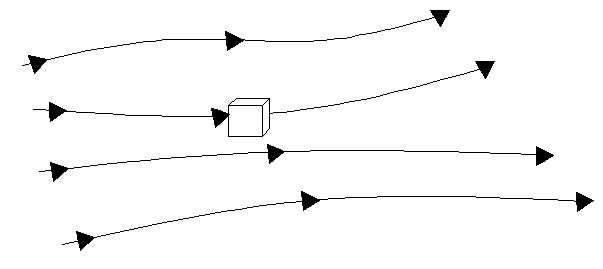
a) Finite control volume moving along with the flow
b) Infinitesimally small element moving along with the flow
c) Infinitesimally small element with the fluid passing through it
d) Stationary finite control volume
View Answer
Explanation: The small cube represents an infinitesimally small fluid element. This cube is moving. It represents an infinitesimally small element moving along with the flow.
10. A stationary model will result in ____________
a) Differential equation
b) Non-conservative equation
c) Conservative equation
d) Integral equation
View Answer
Explanation: A stationary model has its position coordinates independent of time. This gives a conservative equation without any substantial derivative.
11. A model of fluid moving along with the flow gives non-conservative equation. What is the reason?
a) Position coordinates are dependent on time
b) Position coordinates are independent on time
c) Velocity is dependent on time
d) Velocity is independent of time
View Answer
Explanation: As the flow model is not stationary, its position coordinates vary along with time. So, it results in a non-conservative equation.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Chemical Engineering Books
- Practice Chemical Engineering MCQs
- Apply for Mechanical Engineering Internship
- Practice Mechanical Engineering MCQs
- Check Mechanical Engineering Books
