This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “High Resolution Schemes – Normalized Variable Formulation”.
1. The Normalized Variable Formulation (NVF) is used to ___________
a) describe and analyse temporal schemes
b) describe and analyse high-resolution schemes
c) visualize high-resolution schemes
d) visualize temporal scheme
View Answer
Explanation: The Normalized Variable Formulation (NVF) is used for the description and analysis of high-resolution schemes. The Normalized Variable Diagram (NVD) is used for visualizing the high-resolution schemes.
2. The NVF approach does not rely on _____________
a) far downwind node
b) far upwind node
c) upwind node
d) downwind node
View Answer
Explanation: The NVF is a face formulation procedure based on normalizing the dependent variable for which the flow variable at the face has to be constructed. The NVF approach relies upon the upwind, downwind and far upwind nodes.
3. Consider the following diagram.
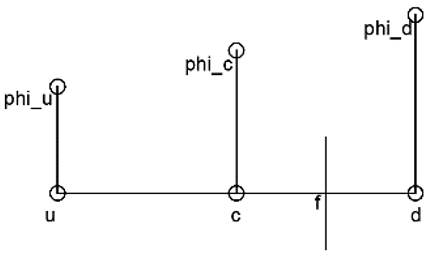
In the diagram,
phi_u → Φu
phi_d → Φd
phi_c → Φc
Find the normalized flow variable \((\tilde{\phi_f})\) at the face f as in the NVF approach.
a) \(\tilde{\phi_f}=\frac{(\phi_f-\phi_c)}{(\phi_f-\phi_u)}\)
b) \(\tilde{\phi_f}=\frac{(\phi_f-\phi_u)}{(\phi_c-\phi_u)}\)
c) \(\tilde{\phi_f}=\frac{(\phi_f-\phi_c)}{(\phi_d-\phi_c)}\)
d) \(\tilde{\phi_f}=\frac{(\phi_f-\phi_u)}{(\phi_d-\phi_u)}\)
View Answer
Explanation: Normalization is a procedure of non-dimensionalizing a variable. In the NVF approach, the flow variable (Φf) is normalized as
\(\tilde{\phi_f}=\frac{(\phi_f-\phi_u)}{(\phi_d-\phi_u)}\) Where,
Φu → Flow variable at the far upwind node.
Φd → Flow variable at the downwind node.
Φc → Flow variable at the upwind node.
4. What are the normalized values of the variables Φd (downwind) and Φu (far upwind)?
a) 1 and 0
b) 0 and ∞
c) 1 and ∞
d) 0 and 1
View Answer
Explanation: From the normalization formula,
\(\tilde{\phi_d}=\frac{\phi_d-\phi_u}{\phi_d-\phi_u}=1\).
\(\tilde{\phi_u}=\frac{\phi_u-\phi_u}{\phi_d-\phi_u}=0\).
5. Which of these conditions represent a monotonic profile of variable Φ between the far upwind node and downwind node?
(Note: \(\tilde{\phi_c}\) is the normalized flow variable at the upwind node).
a) \(1\leq\tilde{\phi_c}\leq ∞\)
b) \(0\leq\tilde{\phi_c}\leq 1\)
c) \(0\leq\tilde{\phi_c}\leq 0.5\)
d) \(0.5\leq\tilde{\phi_c}\leq 1\)
View Answer
Explanation: For a variable Φ to have a monotonic profile,
\(\tilde{\phi_u}\leq\tilde{\phi_c}\leq\tilde{\phi_d}\)
But, \(\tilde{\phi_u}=0 \,and\, \tilde{\phi_d}=1.\) So,
\(0\leq\tilde{\phi_c}\leq 1.\)
6. If \(\tilde{\phi_c}<0 \,or\, \tilde{\phi_c}>1\), what does it mean?
(Note: \(\tilde{\phi_c}\) is the normalized flow variable at the upwind node).
a) Maximum at c
b) Minimum at c
c) Extremum at c
d) Global minimum at c
View Answer
Explanation: According to the NVF approach, the value of \(\tilde{\phi_{c}}\) should be bounded between 0 and 1. If this is not the case, either local maximum or local minimum exists at the upwind node. In general, we can say that the upwind node gets an extremum.
7. What is the normalized flow variable at the face (\(\tilde{\phi_f}\)) for the upwind and downwind schemes respectively?
(Note: \(\tilde{\phi_c}\) is the normalized flow variable at the upwind node).
a) 1 and 0
b) 1 and \(\tilde{\phi_c}\)
c) 0 and 1
d) \(\tilde{\phi_c}\) and 1
View Answer
Explanation: For the upwind scheme,
\(\phi_f=\phi_c⟹\tilde{\phi_f}=\tilde{\phi_c}.\) For the downwind scheme,
\(\phi_f=\phi_d \Rightarrow \tilde{\phi_f}=1.\) Where,
Φf → Flow variable at the face.
Φc → Flow variable at the upwind node.
Φd → Flow variable at the downwind node.
\(\tilde{\phi_f}, \tilde{\phi_c}\) → Normalized flow variables at respective nodes.
8. Normalize the following equation.
\(\phi_f=\phi_c+\frac{\phi_d-\phi_u}{4}\)
Where,
Φf → Flow variable at the face.
Φc → Flow variable at the upwind node.
Φd → Flow variable at the downwind node.
Φu → Flow variable at the far upwind node.
a) \(\tilde{\phi_f}=\tilde{\phi_c}+\frac{1}{4}\)
b) \(\tilde{\phi_f}=\frac{\tilde{\phi_c}}{4}\)
c) \(\tilde{\phi_f}=1+\frac{\tilde{\phi_c}}{4}\)
d) \(\tilde{\phi_f}=\tilde{\phi_c}+\frac{3}{4}\)
View Answer
Explanation: Normalizing the equation,
\(\tilde{\phi_f} = \frac{\phi_c-\phi_u}{\phi_d-\phi_u}+\frac{\frac{\phi_d-\phi_u}{\phi_d-\phi_u}}{4}-\frac{\frac{\phi_u-\phi_u}{\phi_d-\phi_u}}{4}\)
\(\tilde{\phi_f}=\tilde{\phi_c}+\frac{1}{4}-\frac{0}{4}\)
\(\tilde{\phi_f}=\tilde{\phi_c}+\frac{1}{4}.\)
9. Plotting the QUICK scheme in the (\(\tilde{\phi_c},\tilde{\phi_f}\)) plane, the profile will be ____
(Note: \(\tilde{\phi_c} \,and\, \tilde{\phi_f}\) are the normalized flow variable at the upwind node and at the face respectively).
a) quadratic line
b) straight line
c) curved line
d) a parabola
View Answer
Explanation: The normalized form of the QUICK scheme is
\(\tilde{\phi_f}=\frac{3}{8}+\frac{3}{4}\tilde{\phi_c}.\)
This is of the form \(\tilde{\phi_f}=a+b\tilde{\phi_c}.\) It is a straight line equation. So, the resulting profile will be a straight line.
10. In the Normalized Variable Diagram (NVD), all the second-order and third-order schemes pass through the point ________________
a) (0,1)
b) (0.5,0.5)
c) (0.5, 0.75)
d) (1,1)
View Answer
Explanation: Except for the first-order accurate schemes, the profiles of all the schemes pass through (0.5, 0.75) in the NVD. For a scheme to be second-order accurate, it must pass through this point. For a scheme to be third-order accurate, its slope at the point (0.5, 0.75) should be 0.75.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Chemical Engineering MCQs
- Check Mechanical Engineering Books
- Check Chemical Engineering Books
- Practice Mechanical Engineering MCQs
- Apply for Chemical Engineering Internship
