This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Finite Volume Methods – Order of Accuracy”.
1. For integrating the convective and diffusive fluxes using the mean value approximation, the value at the ___________ is used.
a) face centre
b) cell centre
c) node
d) vertex
View Answer
Explanation: The convective and diffusive fluxes undergo a surface integral. To get the surface integral, they are integrated over the area of the face considered. While approximating using the mean value approximation, the central value is used. So, the value at the face centre is used.
2. For integrating the source term, if the value is approximated using the mean value theorem, the value at the _____________ is used.
a) face centre
b) cell centre
c) boundary face
d) vertex
View Answer
Explanation: Source term integral is a volume integral. Approximating the volume integral, the value at the centre of the cell and the volume of the cell are multiplied. So, the value at the cell centre is used.
3. What is the order of accuracy of the midpoint rule approximation?
a) Fourth-order
b) Third-order
c) Second-order
d) First-order
View Answer
Explanation: The midpoint rule is the method which uses the value of the function only at its midpoint to approximate the integration. It is second order accurate. This is the simplest method of approximation.
4. I know the value of flux at point xc. How will you find the value of this flux at point x away form xc?
a) Simpson’s rule
b) Trapezoidal rule
c) Mean value theorem
d) Taylor series expansion
View Answer
Explanation: Simpson’s rule, Trapezoidal rule and the Mean value theorem are all used to integrate a function numerically. To get a value at the point near another point where the value is known, we use the Taylor series.
5. Which is the order of accuracy used for?
a) To quantify the rate of convergence
b) To find the error
c) To find the stability
d) To find the consistency
View Answer
Explanation: The order of accuracy of a numerical method is used to quantify the rate of convergence of the approximation. This can be applied to both the finite difference and the finite volume methods.
6. In which of these methods the function is assumed to vary linearly with the independent variable?
a) Trapezoidal rule and Simpson’s rule
b) Trapezoidal rule
c) Midpoint rule and Simpson’s rule
d) Only Simpson’s rule
View Answer
Explanation: The trapezoidal rule assumes that the dependent variable varies linearly with the independent variable. So, the mean of the values at the endpoints is taken to calculate the integral value.
7. What is the order of accuracy for the method of numerical approximation represented by this diagram?
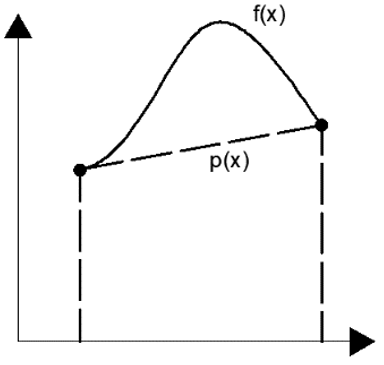
a) Fourth-order
b) Third-order
c) Second-order
d) First-order
View Answer
Explanation: The given diagram represents the Trapezoidal rule for the approximation of an integral. It uses the values at the starting and the ending of the function. The order of accuracy of the Trapezoidal rule is two.
8. Simpson’s rule assumes the function to be ___________
a) constant
b) cubic
c) linear
d) quadratic
View Answer
Explanation: Simpson’s rule assumes the function to be integrated as a quadratic function. The points chosen to generate the quadratic line are the two endpoints and the midpoint. So, this approximation is more accurate.
9. How is the order of accuracy of the mean value approach found?
a) Using spatial variation
b) Using trapezoidal rule
c) Using convergence
d) Using Fourier expansion
View Answer
Explanation: The mean value theorem approximates the function to be linear. If the real spatial variation of the function is found and the two are subtracted, the order of accuracy can be obtained.
10. What is the order of accuracy for the method of numerical approximation represented by this diagram?
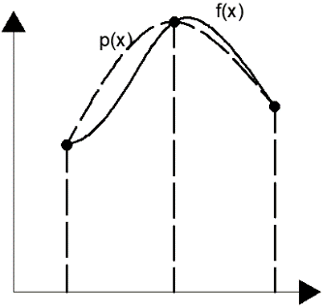
a) second-order
b) fourth-order
c) first-order
d) third-order
View Answer
Explanation: The diagram represents Simpson’s rule of approximation. This rule uses quadratic interpolation of the two endpoints and the midpoint of the function. The order of accuracy of this approximation is four.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Mechanical Engineering Books
- Apply for Chemical Engineering Internship
- Practice Mechanical Engineering MCQs
- Check Computational Fluid Dynamics Books
- Apply for Mechanical Engineering Internship
