This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Structured Grids in FVM”.
1. For a regular structured grid, which of these statements is true?
a) Each interior cell is connected to the same number of neighbours
b) Each cell is connected to the same number of neighbours
c) Each boundary cell is connected to the same number of neighbours as an interior cell
d) Each direction has the same number of cells
View Answer
Explanation: The boundary cells will have less number of neighbours when compared to the interior cells. As the statement telling “Each cell” includes the boundary cells also, it does not hold true. It is not necessary for the structured grids to have the same number of cells in every direction. So, the statement “Each interior cell is connected to the same number of neighbours” is only true.
2. Structured grids give ____________ and need ____________
a) no access to elements, less memory for storage
b) easy access to elements, less memory for storage
c) easy access to elements, more memory for storage
d) no access to elements, more memory for storage
View Answer
Explanation: Structured grids have properly ordered cells. So, it is easy to access their elements or grid points. As access is easy, it is easy to store the values also in memory. So, less memory is required.
3. Topological information is embedded in a structured mesh through ___________
a) neighbours
b) boundaries
c) indices
d) discretization
View Answer
Explanation: The topological (spatial relation) information is embedded in the mesh structure through the indexing system. This also leads to greater efficiency in coding, cache utilization and vectorization.
4. In a three-dimensional structured grid, an element has ____________ faces and ____________ vertices.
a) 8, 6
b) 8, 8
c) 4, 4
d) 6, 8
View Answer
Explanation: The elements of a structured grid are in a hexagonal shape. They have six faces and eight vertices. Each interior element is surrounded by six neighbours. Unlike the unstructured grids, these are fixed in a structured grid.
5. In a two-dimensional grid, the elements are ____________ in shape and have ___________ neighbours.
a) Quadrilateral, 4
b) Cube, 6
c) Cube, 4
d) Cuboid, 4
View Answer
Explanation: For a two-dimensional grid, there are four faces and four vertices for every element. And, each element is surrounded by four elements. With this, we cannot say if they are cubes or cuboids. In general, we can say they will definitely be quadrilaterals.
6. Which is correct?
a) Local index has a single index and global index has multiple indices
b) Global index has a single index and local index has multiple indices
c) Both local and global indices have a single index
d) Both local and global indices have multiple indices
View Answer
Explanation: Local indexing is the indexing of elements around a particular cell. It has to mention the direction also. So, it involves multiple indexing. Global indexing is just a single number representing a cell or element.
7. Consider the two 2-D cells given here.
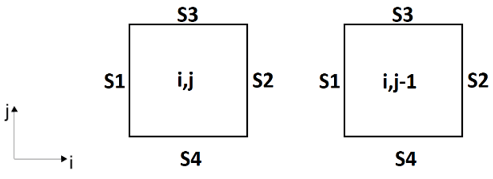
Which of these is correct? (Hint: Each face of an element points outside).
a) S1i,j-1=S2i,j
b) S1i,j-1=-S2i,j
c) S3i,j-1=-S4i,j
d) S3i,j-1=S4i,j
View Answer
Explanation: Arranging these two grids according to the directions of i and j, we get
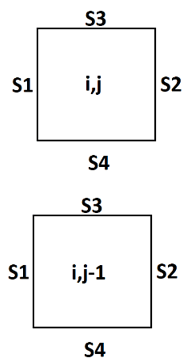
Each surface points outside. But, their magnitude is the same. Therefore,
S3i,j-1=-S4i,j.
8. In structured grids, computer memory is saved by ____________
a) multi-dimensions
b) localization
c) linearization
d) vectorization
View Answer
Explanation: As it is easy to index the elements in structured grids, the values are stored using global indexing which does not need three-dimensional indexing. So, it can be vectorized and saved as a single array of elements. This saves computer memory.
9. The values of the flow variables at the faces can be calculated by _____________ in a structured grid.
a) Interpolation
b) Taylor series
c) Fourier series
d) Shape functions
View Answer
Explanation: As the cells of a structured grid have simple quadrilateral shapes, the values at a cell faces can be easily interpolated using the values of the flow variables at the cell centroids of the two cells sharing that particular face.
10. Which of these represent the discretization indexing?
a) Φi,j+1, Φi,j-1
b) Φe, Φw
c) Φn+1, Φn-1
d) Φi+1,j, Φi-1,j
View Answer
Explanation: Discretization indexing is the type of indexing which is used locally while mentioning the neighbours of an element. Here, Φe is the eastern node; Φw is the western node; Φn is the northern node; Φs is the southern node.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Mechanical Engineering MCQs
- Practice Chemical Engineering MCQs
- Apply for Chemical Engineering Internship
- Check Computational Fluid Dynamics Books
- Check Mechanical Engineering Books
