This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Momentum Equation”.
1. What is the physical principle behind momentum equation?
a) Newton’s second law of motion
b) Newton’s first law of motion
c) Zeroth law of thermodynamics
d) First law of thermodynamics
View Answer
Explanation: Momentum equation is derived using Newton’s second law of motion. This gives a relationship between force and acceleration. It also gives the condition for momentum conservation.
2. Which of these statements hold true?
a) Momentum conservation is applicable to neither individual directions nor the whole system
b) Momentum conservation is applicable to the whole system but not individually
c) Momentum conservation is applicable to both individual directions and the whole system
d) Momentum conservation is applicable only to the three directions individually
View Answer
Explanation: According to newton’s second law, force is equal to the product of mass and acceleration, where force and acceleration are vector quantities (\(\vec{F}=m\vec{a}\)). Thus conservation is applicable to the whole system in vector terms and also to the individual directions.
3. Consider an element shown below. S is the source term.
If gravitational force is the only force acting on this element. Which of these following is correct?
a) Sx=mg, Sy=0, Sz=mg
b) Sx=0, Sy=0, Sz=mg
c) Sy=0, Sz=0, Sx=mg
d) Sz=0, Sx=0, Sy=mg
View Answer
Explanation: For momentum equation, source is the body force of the element. If gravity is the only force acting on the element, then source=mass×acceleration due to gravity. This will act only in the y-direction.
4. Consider the element shown in the diagram. In diagram,
p → pressure
\(p+\frac{\Delta p}{\Delta x}dx=p+\frac{\partial p}{\partial x}dx\)
dx, day, dz → dimensions in x, y and z directions
What is the net pressure force in x direction?
a) \(-\frac{\partial p}{\partial x}\)
b) \(\frac{\partial p}{\partial x}\)
c) \(\frac{\partial p}{\partial x}dx \,dy \,dz\)
d) \(-\frac{\partial p}{\partial x}dx \,dy \,dz\)
View Answer
Explanation: From the diagram,
pressure force= pressure×area
inlet pressure force in x-direction = p×dy dz
outlet pressure force in x-direction = -(p+\(\frac{\partial p}{\partial x}\)dx)dydz
net pressure force in x-direction = (p×dy dz)-(p+\(\frac{\partial p}{\partial x}\)dx)dydz
net pressure force in x-direction=\(-\frac{\partial p}{\partial x}dx \,dy \,dz\)
5. The physical property Φ of the general transport equation is replaced by ________ to get momentum equation.
a) Velocity vector
b) Mass
c) Force vector
d) Acceleration vector
View Answer
Explanation: The physical property in general transport equation should be replaced by velocity vector. This will result in momentum equation. For mass conservation, Φ = 1. For momentum (mass×velocity) conservation, Φ = 1×\(\vec{V}=\vec{V}\).
6. The source term in the momentum equation is ________
a) Pressure force
b) Body forces
c) Viscous force
d) Acceleration
View Answer
Explanation: The effect of surface forces are external. They are not produced inside the body. Body forces are created inside the body of conservation. So, the body force term is the source term.
7. I am using an infinitesimally small element of fluid moving along with the flow as my model. What is the acceleration of this model in x-direction?
a) \(a_x=\frac{D\vec{V}}{Dt}\)
b) \(a_x=\frac{\partial \vec{V}}{\partial t}\)
c) \(a_x=\frac{Du}{Dt}\)
d) \(a_x=\frac{\partial u}{\partial t}\)
View Answer
Explanation: Acceleration is the rate of change of velocity. Acceleration in the x-direction is the rate of change of velocity in x-direction (u). As the model is moving, rate of change is given by substantial derivative. Thus the acceleration in x-direction is \(a_x=\frac{Du}{Dt}\).
8. When I derived the momentum equation in x-direction, I got this equation (directly without any manipulation)\( \rho\frac{Du}{Dt}=-\frac{\partial p}{\partial x}+\frac{\partial \tau_{xx}}{\partial x}+\frac{\partial \tau_{yx}}{\partial y}+\frac{\partial \tau_{zx}}{\partial z}+\rho f_x\). Which of these models have I used?
a) 
b) 
c) 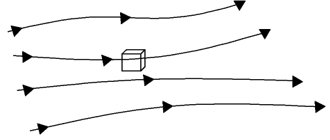
d) 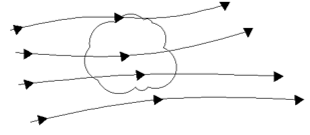
View Answer
Explanation: My equation is differential non-conservative. So, I must have used an infinitesimally small element moving along with the flow.
9. The momentum equation is \( \rho\frac{Du}{Dt}=-\frac{\partial p}{\partial x}+\frac{\partial \tau_{xx}}{\partial x}+\frac{\partial \tau_{yx}}{\partial y}+\frac{\partial \tau_{zx}}{\partial z}+\rho f_x\). Which of these statements about sign convention can be inferred from this equation?
a) Pressure force is taken as negative
b) Tensile force is taken as negative
c) Pressure force is taken as positive
d) Pressure force is unsigned
View Answer
Explanation: When all the other forces and accelerations are positive, gradient of pressure force is negative(-\(\frac{\partial p}{\partial x}\)). This is possible only when pressure force is signed posititve.
10. Which of these terms represent convection in the momentum equation?
a) \(div(u\vec{V})\)
b) \(div(\rho \vec{V})\)
c) \(\nabla .(u\vec{V})\)
d) \(div(\rho u\vec{V})\)
View Answer
Explanation: : From general conservation equation, the convection term is div(ρuΦ). For momentum equation, \(\Phi=\vec{V}\). So, the convection term in momentum equation is div(ρu\(\vec{V}\)).
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Mechanical Engineering Books
- Practice Mechanical Engineering MCQs
- Apply for Chemical Engineering Internship
- Practice Chemical Engineering MCQs
- Apply for Mechanical Engineering Internship
