This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “The Geometry of FVM Elements”.
1. How are the faces of a 3-D element divided to find the area?
a) Squares
b) Quadrilaterals
c) Rectangles
d) Triangles
View Answer
Explanation: The faces of a 3-D element are 2-D polygons. With the intention of finding the area of these faces, they are divided into triangles of different type and sizes. Triangles give the advantage of having any length in all three of its sides.
2. Which of these points form the apex of the sub-elements of the faces?
a) Centre of mass of the face
b) Vertex of the face
c) Geometric centre of the face
d) Apex of the face
View Answer
Explanation: The sub-elements are all triangular in shape. The apex of these triangles are all the same point. The geometric centre of the face is chosen as the apex of the triangles. The geometric centre is not the centroid of the polygon.
3. Which formula is suitable for finding the geometric centre of a polygonal face?
a) \(\frac{1}{No.of points}\sum_{i=1}^{No.of points}\) Point defining the polygoni
b) \(\sum_{i=1}^{No.of\, points}\) Point defining the polygoni
c) \(\frac{1}{Point\, defining\, the\, polygon}\sum_{i=1}^{No.of\, points}\) Point defining the polygoni
d) \(\frac{1}{No.of\, points}\sum_{i=1}^{No.of\, points}\)Centroidi
View Answer
Explanation: The average of all the points that define the polygon is the geometric centre of the polygon. Therefore,
Geometric centre=\(\frac{1}{No.of points}\sum_{i=1}^{No.of points}\) Point defining the polygoni
4. Which of these formulae is used to find the area of the sub-elements in CFD?
a) Vector product of two sides
b) Half of the vector product of two sides
c) Half of the base times height
d) Half of the vector product of all three sides
View Answer
Explanation: Sub-elements are in triangular shape. Half of the base times height is the formula generally used to find the area of a triangle. But, CFD uses the vector-based formula to make it algorithmically easier, which is given by half of the vector product of two sides.
5. The centroid of the faces of a 3-D element is obtained by _________
a) Area-weighted average of the sub-elements
b) Average of the sub-elements
c) Area-weighted average of the centroid of the sub-elements
d) Volume-weighted average of the centroid of the sub-elements
View Answer
Explanation: The centroid of each of the sub-elements are first located. The weighted average of these centroids is the centroid of the whole face. Areas of the triangles are used as the weight for this average.
6. The surface area of the face of a 3-D element is a _____________
a) 3-D tensor
b) 2-D tensor
c) Scalar
d) Vector
View Answer
Explanation: The surface area of the face of a 3-D element is a vector with the area as its magnitude and pointing in a direction. This direction decides if the face points outwards or inwards. Moreover, the area is the result of the cross product of two vectors which will again be a vector.
7. How is it identified whether a vector is pointing outwards or inwards?
a) Sign of the vector joining the element’s centroid with the face’s centroid is used
b) Sign of the surface vector is used
c) Cross product of the surface vector and the vector joining the element’s centroid with the face’s centroid
d) Dot product of the surface vector and the vector joining the element’s centroid with the face’s centroid
View Answer
Explanation: The vector joining the centroid of the element with the centroid of the face always points outwards. So, the dot product of this vector with the surface vector is found. If the sign of the dot product is positive, the surface vector points outwards. Otherwise, it points inwards.
8. I know the value of the flow variable at two points. In which of these cases, is it easy for me to calculate the flow variable at a point between these two?
a) Three-dimensional FVM
b) Two-dimensional FVM
c) One-dimensional FVM
d) Two-dimensional FDM
View Answer
Explanation: If the values at two points are known, in the one-dimensional case, it is easy to find the values at any other point. In the two-dimensional and three-dimensional cases, they pose complication to the calculation.
9. To find the value of a flow variable at a third point in between two points with known values, which of these methods can be used for the one-dimensional case?
a) Shape function
b) Interpolation
c) Taylor series
d) Fourier series
View Answer
Explanation: If the value of the flow variable is known at two points and the value at the third point which lies in between these two is to be found, simple interpolation will be enough in the one-dimensional case. The value at any point in between these two points can be found using these two points.
10. Consider the diagram.
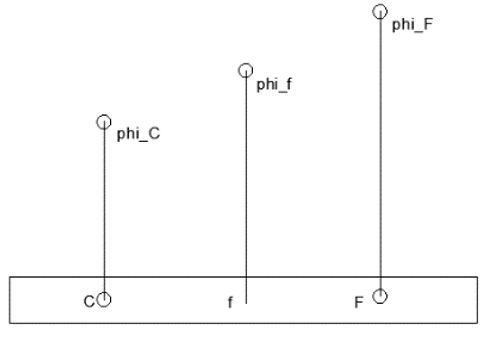
When is the formula Φf=gfΦF+(1-gf)Φc; gf=\(\frac{distance_{cf}}{distance_{cf}+distance_{fF}}\) valid?
a) Only if Φ varies linearly
b) Only if Φ varies quadratically
c) Only if Φ varies cubically
d) Always
View Answer
Explanation: The formula Φf=gfΦF+(1-gf)Φc; gf=\(\frac{distance_{cf}}{distance_{cf}+distance_{fF}}\) is the linear interpolation formula to find Φf. If the variation of Φ is not linear (the three points Φf, Φc and ΦF are not collinear), the formula becomes invalid.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Mechanical Engineering Books
- Practice Chemical Engineering MCQs
- Apply for Mechanical Engineering Internship
- Check Computational Fluid Dynamics Books
- Check Chemical Engineering Books
