This set of Computational Fluid Dynamics written test Questions & Answers focuses on “Continuity Equation – Infinitesimally Small Element”.
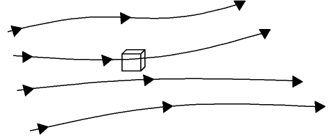
1. Which of the equations suit this model?
a) \(\frac{\partial}{\partial t}\iiint_V\rho dV + \iint_s \rho \vec{V}.\vec{dS} = 0\)
b) \(\frac{D}{Dt}\iiint_V\rho dV = 0\)
c) \(\frac{\partial\rho}{\partial t}+\nabla.(\rho \vec{V})=0\)
d) \(\frac{D\rho}{Dt}+\rho \nabla.\vec{V}=0\)
View Answer
Explanation: The diagram represents infinitesimally small fluid element fixed in space. This model will give conservative differential equation which is \(\frac{\partial\rho}{\partial t}+\nabla.(\rho \vec{V})=0\) from the options.
2. Consider an infinitesimally small fluid element with density ρ (of dimensions dx, dy and dz) fixed in space and fluid is moving across this element with a velocity \(\vec{V}=u\vec{i}+v\vec{j}+w\vec{k}\). The net mass flow across the fluid element is given by ______
a) \([\frac{\partial(\rho u)}{\partial x} + \frac{\partial(\rho v)}{\partial y} + \frac{\partial(\rho w)}{\partial z}]dx \,dy \,dz\)
b) \([\frac{\partial(\rho u)}{\partial x} + \frac{\partial(\rho v)}{\partial y} + \frac{\partial(\rho w)}{\partial z}]\)
c) [ρ]dx dy dz
d) \([\frac{\partial(\rho)}{\partial x} + \frac{\partial(\rho)}{\partial y} + \frac{\partial(\rho)}{\partial z}]dx \,dy \,dz\)
View Answer
Explanation: Mass inflow in x direction=(ρu)dy dz
mass outflow in x direction=\((\rho u+\frac{\partial(\rho u)}{\partial x} dx)dy \,dz\)
change in mass flow in x direction=\((\rho u+\frac{\partial(\rho u)}{\partial x} dx)dy \,dz-(\rho u)dy dz\)
change in mass flow in x direction=\(\frac{\partial(\rho u)}{\partial x} dx \,dy \,dz\)
Net mass flow across the element = (change in mass flow in x direction + change in mass flow in y direction + change in mass flow in z direction)
= \(\frac{\partial(\rho u)}{\partial x} dx \,dy \,dz + \frac{\partial(\rho v)}{\partial y} dx \,dy \,dz + \frac{\partial(\rho w)}{\partial z} dx \,dy \,dz\)
Net mass flow across the element = \(\Big[\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}+\frac{\partial(\rho w)}{\partial z}\Big]dx \,dy \,dz\)
3. Consider an infinitesimally small fluid element with density ρ (of dimensions dx, dy and dz) fixed in space and fluid is moving across this element with a velocity \(\vec{V} = u\vec{i} + v\vec{j} + w\vec{k}\). The rate of change in mass of the fluid element is given by ____________
a) \(\frac{\partial(\rho u)}{\partial x} + \frac{\partial(\rho v)}{\partial y} + \frac{\partial(\rho w)}{\partial z}\)
b) \(\frac{\partial \rho}{\partial t}\)
c) \(\frac{\partial\rho}{\partial t}(dx \,dy \,dz) \)
d) \([\frac{\partial(\rho u)}{\partial x} + \frac{\partial(\rho v)}{\partial y} + \frac{\partial(\rho w)}{\partial z}]dx \,dy \,dz\)
View Answer
Explanation: Mass=density × volume
mass of fluid element=ρ×dx dy dz
rate of change in mass of fluid element=\(\frac{\partial\rho}{\partial t}dx \,dy \,dz \)
4. According to the conservation law, “Net mass flow across the fluid element is equal to the rate of change of mass inside the element”. But, stating the final equation, “Net mass flow across the fluid element + the rate of change of mass inside the element = 0”. Why is the operation not subtraction?
a) Irrespective of the law, the sum is always zero
b) The two terms are always opposite in sign
c) Change in sign is not considered
d) Rate of change may be increase or decrease
View Answer
Explanation: The “net mass flow across the fluid element” being positive means that it is outward flow. If flow is outward, mass inside the fluid element decreases leading to a negative “rate of change of mass inside the element”. Thus, the two terms are always opposite in sign that they can be summed up to get zero.
5. Consider an infinitesimally small fluid element with density ρ (of dimensions dx, dy and dz) fixed in space and fluid is moving across this element with a velocity \(\vec{V}=u\vec{i}+v\vec{j}+w\vec{k}\). What is the final reduced form of net mass flow across the fluid element?
a) \(\frac{\partial\rho}{\partial t}\)
b) \(\rho\vec{V} dx \,dy \,dz\)
c) \(\nabla.(\rho\vec{V})\)
d) \(\nabla.(\rho\vec{V})\)dx dy dz
View Answer
Explanation:
Net mass flow across the element = change in mass flow in x direction + change in mass flow in y direction + change in mass flow in z direction
= \(\frac{\partial(\rho u)}{\partial x} dx \,dy \,dz + \frac{\partial(\rho v)}{\partial y} dx \,dy \,dz + \frac{\partial(\rho w)}{\partial z} dx \,dy \,dz \)
=\(\left[(\frac{\partial}{\partial x}\vec{i}+\frac{\partial}{\partial y}\vec{j}+\frac{\partial}{\partial z}\vec{k})dx \,dy \,dz.((\rho u)\vec{i} + (\rho v)\vec{j} + (\rho w)\vec{k})\right] \)
Net mass flow across the element = \([\nabla.(\rho \vec{V})]dx \,dy \,dz\).
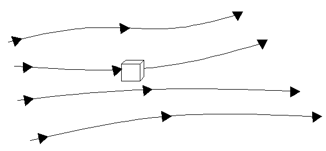
6. Which of the equations suit this model?
a) \(\frac{\partial}{\partial t}\iiint_V\rho dV + \iint_s \rho \vec{V}.\vec{dS} = 0\)
b) \(\frac{D}{Dt}\iiint_V\rho dV = 0\)
c) \(\frac{D\rho}{Dt}+\rho \nabla.\vec{V}=0\)
d) \(\frac{\partial\rho}{\partial t}+\nabla.(\rho \vec{V})=0\)
View Answer
Explanation: \(\frac{\partial\rho}{\partial t}+\nabla.(\rho \vec{V})=0\) is the non-conservative differential equation. Non-conservative differential equation is given by an infinitesimally small fluid element moving along with the flow.
7. Consider an infinitesimally small fluid element with density ρ (of dimensions dx, dy and dz with mass δ m and volume δ V) moving along with the flow with a velocity \(\vec{V}=u\vec{i}+v\vec{j}+w\vec{k}\). What is the time rate of change of mass of this element?
a) \(\frac{D(\rho \delta V)}{Dt}\)
b) \(\frac{\partial(\rho \delta m)}{\partial t}\)
c) \(\frac{\partial(\rho \delta V)}{\partial t}\)
d) \(\frac{D(\rho \delta m)}{Dt}\)
View Answer
Explanation: Substantial derivative is used as the model is moving.
mass = ρ δ V
time rate of change of mass=\(\frac{D(\rho \delta V)}{Dt}\)
8. Consider an infinitesimally small fluid element with density ρ (of dimensions dx, dy and dz with mass δ m and volume δ V) moving along with the flow with a velocity \(\vec{V}=u\vec{i}+v \vec{j}+w\vec{k}\). The continuity equation is \(\frac{D\rho}{Dt}+\rho \nabla.\vec{V}=0\). Where does this second term come from?
a) Integral
b) The rate of change of element’s volume
c) Elemental change in mass
d) Local derivative
View Answer
Explanation: Applying mass conservation for this element,
time rate of change of mass = 0
\(\frac{D(\rho \delta V)}{Dt}=0 \)
\(\delta V \frac{D(\rho)}{Dt}+\rho\frac{D(\delta V)}{Dt}=0 \)
\(\frac{D(\rho)}{Dt}+\rho\frac{1}{\delta V}\frac{D(\delta V)}{Dt}=0 \)
\(\frac{D(\rho)}{Dt}+\rho\nabla.\rho=0 \)
Thus, the term arises from the rate of change of element’s volume.
9. Consider the continuity equation \(\frac{\partial\rho}{\partial t}+\nabla.(\rho \vec{V})=0\). For an incompressible flow, this equation becomes ___________
a) \(\nabla.(\rho \vec{V})=0\)
b) \(\frac{\partial(\rho\vec{V})}{\partial t}=0\)
c) \(div(\vec{V})=0\)
d) \(div(\rho\vec{V})=0\)
View Answer
Explanation: Taking the continuity equation,
\(\frac{\partial\rho}{\partial t}+\nabla.(\rho \vec{V})=0\)
For incompressible flow, ρ is constant
\(\frac{\partial\rho}{\partial t}+\nabla.(\rho \vec{V})=0\)
The resulting equation is
\(\nabla.(\rho \vec{V})=0\)
\(\rho\nabla.(\vec{V})=0\)
\(\nabla.(\vec{V})=0\)
Thus, for incompressible flow, divergence of \(\vec{V}=0\).
10. Consider the continuity equation \(\frac{\partial\rho}{\partial t}+\nabla.(\rho \vec{V})=0\). For a steady flow this equation becomes ___________
a) \(\nabla.(\rho \vec{V})=0\)
b) \(\nabla.(\vec{V})=0\)
c) \(div(\vec{V})=0\)
d) \(curl(\vec{V})=0\)
View Answer
Explanation: Taking the continuity equation,
\(\frac{\partial\rho}{\partial t}+\nabla.(\rho \vec{V})=0\)
For steady flow, flow variables do not vary with time.
\(\frac{\partial\rho}{\partial t}=0\)
Thus, for steady flow \(\nabla.(\rho \vec{V})=0\).
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all written questions on Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Chemical Engineering Books
- Practice Mechanical Engineering MCQs
- Apply for Chemical Engineering Internship
- Practice Chemical Engineering MCQs
- Check Computational Fluid Dynamics Books
