This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Governing Equations – Eulerian and Lagrangian Conservation Laws”.
1. The principle of conservation is applicable to _______ systems.
a) isolated system
b) closed system
c) open system
d) all the systems irrespective of its type
View Answer
Explanation: The principle of conservation is applicable only to the systems where there will not be any transfer of matter or energy. Isolated system will have these characters.
2. The fluid is subdivided into fluid parcels and every fluid parcel is followed as it moves through space and time. Which kind of formulation is this?
a) Cartesian
b) Eulerian
c) Lagrangian
d) Euclidian
View Answer
Explanation: In Lagrangian fluid flow specification, the fluid is subdivided into many parts and each of this part is followed. These parts are called fluid parcels.
3. Each parcel in the Lagrangian formulation is tagged using __________
a) time-dependent position vector
b) time-independent position vector
c) time-dependent velocity vector
d) time-independent velocity vector
View Answer
Explanation: The tag is time-independent so that the tag does not vary along with the flow. Position vector is chosen to follow the parcel along its position.
4. Which of these will best define positions of the parcel in increasing time?
a) Streamline
b) Streakline
c) Boundary line
d) Pathline
View Answer
Explanation: Pathline is the one which represents the path of a fluid element along its way. So, to define the positions of the parcels, pathline is the best.
5. Which of these is an acceptable tag for Lagrangian parcels?
a) Parcel’s centre of mass at instantaneous time
b) Parcel’s centre of pressure at instantaneous time
c) Parcel’s centre of mass at initial time
d) Parcel’s centre of pressure at initial time
View Answer
Explanation: Parcel’s centre of pressure is not suitable as it depends not only on position but on many variables too. Instantaneous time continuously varies along with the path. So, it cannot be a tag.
6. According to Eulerian approach, which of these is correct?
a) Both location and fluid move
b) Location moves and fluid is stationary
c) Both location and fluid are stationary
d) Location is stationary and fluid moves
View Answer
Explanation: According to Eulerian approach, a particular location is chosen and the fluid flows past this location. This flowing fluid is analysed.
7. The independent variables in Eulerian approach are __________ and __________
a) instantaneous time and instantaneous position
b) initial time and instantaneous position
c) instantaneous time and Initial position
d) initial time and initial position
View Answer
Explanation: Current position and time are the variables on which other variables depend on in Eulerian approach. These are the independent variables.
8. In Lagrangian approach, the flow parcels follow __________
a) pressure field
b) velocity field
c) temperature field
d) density field
View Answer
Explanation: Velocity field defines the motion of fluid. Parcels also follow the same path of the fluid and therefore, parcels can be said to follow the velocity field.
9. Let,
t → Instantaneous time
\( \vec{v} \) → Velocity in x-direction
\( \vec{x} \) → Instantaneous position
\( \vec{x_0} \)→ Initial position
The relationship between Eulerian and Lagrangian approaches for velocity in x direction is given by _______
a) \( \vec{v}(t, \vec{x}(\vec{x_0}, t)) = \frac{\partial \vec{x} (\vec{x_0}, t)}{\partial t} \)
b) \( \vec{v}(t, \vec{x}(\vec{x_0}, t)) = \frac{\partial \vec{x_0} (\vec{x}, t)}{\partial t} \)
c) \( \vec{v}(t, \vec{x_0}(\vec{x}, t)) = \frac{\partial \vec{x} (\vec{x_0}, t)}{\partial t} \)
d) \( \vec{v}(t, \vec{x_0}(\vec{x}, t)) = \frac{\partial \vec{x_0} (\vec{x}, t)}{\partial t} \)
View Answer
Explanation: Location at any instantaneous time is
\(\vec{x}(\vec{x_0}, t) \)
Velocity of fluid flow in Lagrangian approach is
\( \frac{\partial \vec{x}(\vec{x_0}, t)}{\partial t}\)
Velocity of fluid flow in Eulerian approach is
\( \vec{x}(t, \vec{x} (\vec{x_0}, t)) \)
The relationship between the approaches is
\(\vec{x}(t, \vec{x} (\vec{x_0}, t)) = \frac{\partial \vec{x}(\vec{x_0}, t)}{\partial t} \).
10. Which of the following frame of references does this diagram represent?
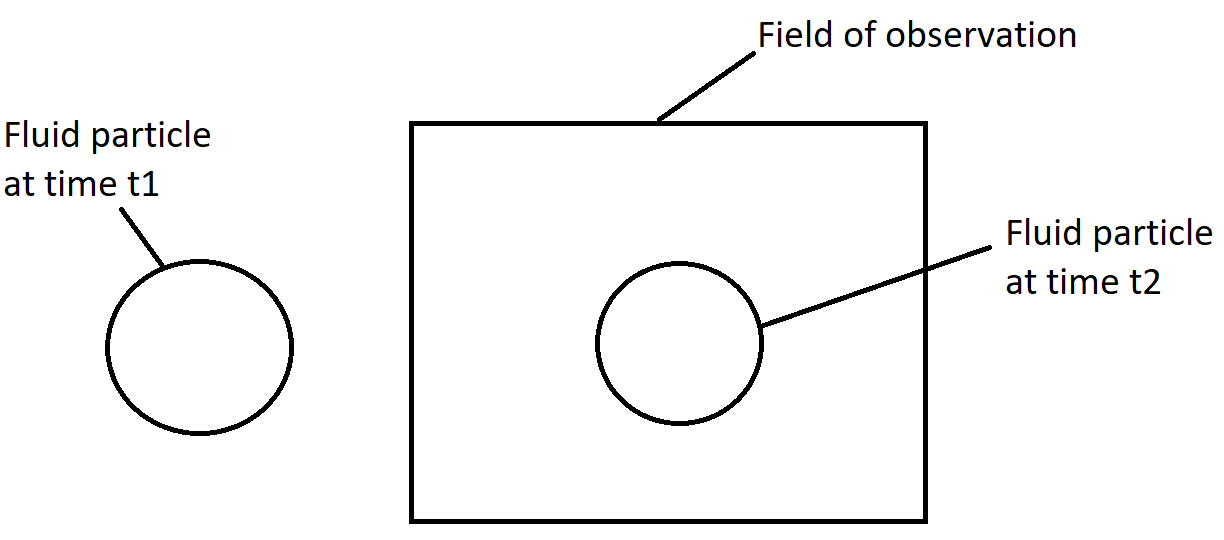
a) Polar
b) Cartesian
c) Lagrangian
d) Eulerian
View Answer
Explanation: In diagram, fluid particles move and the field of observation remains in the same position. This represents Eulerian Approach.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Chemical Engineering Books
- Check Mechanical Engineering Books
- Apply for Chemical Engineering Internship
- Practice Mechanical Engineering MCQs
- Check Computational Fluid Dynamics Books
