This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “High-Resolution Schemes”.
1. A high-resolution scheme is __________
a) a higher order bounded scheme
b) a first-order accurate scheme
c) a first-order bounded scheme
d) a higher-order unbounded scheme
View Answer
Explanation: The high-resolution scheme is a combination of a higher-order profile and the Convection Boundedness Criterion (CBC) to get the most out of it. So, it can be called a higher order bounded scheme.
2. Which of these techniques cannot be used to implement a high-resolution scheme?
a) DC technique
b) DWF method
c) NWF method
d) TVD method
View Answer
Explanation: The deferred correction, Downwind Weighing Factor (DWF) and Upwind Weighing Factor (UWF) are all methods to implement the higher-order and high-resolution schemes. TVD scheme is not used for this purpose.
3. A high-resolution scheme is the best suited for ___________
a) Turbulent flows
b) Problems involving shocks
c) Incompressible flows
d) Unsteady flows
View Answer
Explanation: A normal first-order scheme produces accurate results for flows involving high discontinuities like shocks at the cost of increased grid points. This problem is overcome by high-resolution schemes.
4. Which of these diagrams are used to visualize the high-resolution scheme?
a) Leonard diagram and NVD
b) Cumulative flow diagram and NVD
c) Sweby’s diagram and NVD
d) Cumulative flow diagram and Sweby’s diagram
View Answer
Explanation: The NVD (Normalized Variable Diagram) and Sweby’s diagram are used for visualizing the high-resolution schemes in the NVF and TVD formulation respectively. They can be used to visualize the flux limiters.
5. Which of these is not a high-resolution scheme?
a) MINMOD
b) SMART
c) SIMPLE
d) MUSCL
View Answer
Explanation: The MINMOD scheme, SMART scheme and MUSCL scheme are all high-resolution schemes. SIMPLE is an algorithm which is used to solve the Navier-Stokes equations used for pressure linked equations. It is not a high-resolution scheme.
6. To construct a high-resolution scheme, the monotonic profile in the range 0\(\leq\widetilde{\phi_c}\leq\)1 should pass through __________ in the NVD.
a) points (0,0) and (0,1)
b) points (1,0) and (1,1)
c) points (0,1) and (1,1)
d) points (0,0) and (1,1)
View Answer
Explanation: In the NVD diagram, the monotonic profile in the range 0\(\leq\widetilde{\phi_c}\leq\)1 should connect the points (0,0) and (1,1) for a high-resolution scheme to be constructed. For the other ranges, the profile should follow the upwind scheme.
7. High-resolution schemes give ___________
a) solution without oscillations
b) highly converging
c) inconsistent solutions
d) unstable solution
View Answer
Explanation: The high-resolution schemes are bounded in the sense that they result in solutions which are free from wiggles or oscillations. This the main advantage of the high-resolution schemes over the other schemes.
8. For a high-resolution scheme to have good convergence, the profile in the NVD frame should __________
a) involve sharp angles
b) avoid sharp angles
c) be smooth
d) be differentiable
View Answer
Explanation: A high-resolution scheme can have composite nature of profiles in the NVD frame which involves cut. But, at these cuts, the angle should not be sharp for the schemes to have better convergence.
9. The SMART scheme is constructed using the ____________
a) SUPERBEE scheme
b) STOIC scheme
c) QUICK scheme
d) MINMOD scheme
View Answer
Explanation: The SMART scheme is constructed using the QUICK scheme. The SMART scheme can be easily modified to get a higher convergence. This modification is done by modifying the vertical portion of the profile of the SMART scheme.
10. The diagram represents the NVD of a high-resolution scheme.
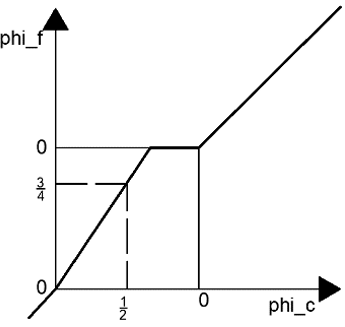
In the diagram, φc = \(\widetilde{\phi_c}\) and φf=\(\widetilde{\phi_f}\).
Identify the scheme.
a) MINMOD
b) SMART
c) STOIC
d) OSHER
View Answer
Explanation: The OSHER scheme in NVD terms is given by
\(\widetilde{\phi_f} = \left\{\begin{matrix}
\frac{3}{2} \widetilde{\phi_c} & 0\leq\widetilde{\phi_c} \leq \frac{2}{3} \\
1 & \frac{2}{3}\leq\widetilde{\phi_c} \leq 1\\
\widetilde{\phi_c} & elsewhere
\end{matrix}\right\}\)
This is represented by the given diagram.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Chemical Engineering Internship
- Apply for Mechanical Engineering Internship
- Check Computational Fluid Dynamics Books
- Practice Mechanical Engineering MCQs
- Practice Chemical Engineering MCQs
