This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Governing Equations – Stress and Strain Tensor”.
1. Which among these forces used in momentum equation is a tensor?
a) Gravitational forces
b) Pressure forces
c) Viscous forces
d) Electromagnetic forces
View Answer
Explanation: Viscous forces are tensors. The other forces given here (Gravitational, viscous and electromagnetic forces) are vectors.
2. What do the two subscripts of stress tensors represent?
a) Directions of stress and strain
b) Directions of stress and normal to the surface on which they are acting
c) Directions of strain and normal to the surface on which they are acting
d) Direction of stress and the flow direction
View Answer
Explanation: The two subscripts of stress tensors indicate the direction of the stress and that of the normal to the surface on which they act. So, stress tensors give the location and direction of the stresses.
3. Which of these fluids have their stress tensor linearly varying to the strain rate?
a) 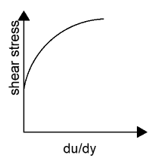
b) 
c) 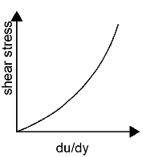
d) 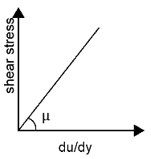
View Answer
Explanation: S-tress tensor linearly varies with the strain rate only for Newtonian fluids. For Newtonian fluid shear stress is proportional to du/dy. In the other cases, shear stress varies non-linearly with du/dy.
4. Which of the stress tensors from the diagram is represented by Τxy?
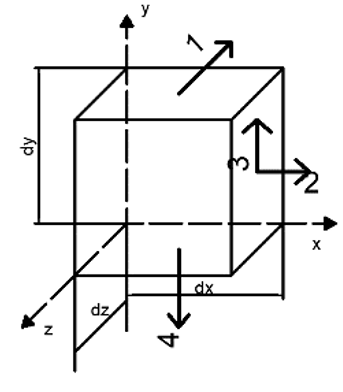
a) 3
b) 2
c) 1
d) 4
View Answer
Explanation: Τxy indicate that the stress component acts in the y-direction on a surface normal to the x-direction. Representing this in the diagram, 3 is the corresponding tensor.
5. The divergence of the stress tensor is _____
a) Scalar
b) Vector
c) 0
d) 1
View Answer
Explanation: Stress tensor is a square matrix given by
Τxy = \(\begin{bmatrix}
\tau_{xx} & \tau_{xy} & \tau_{xz} \\
\tau_{yx} & \tau_{yy} & \tau_{yz} \\
\tau_{zx} & \tau_{zy} & \tau_{zz}
\end{bmatrix}\)
The divergence of this will result in a vector
∇. Τ= \(\begin{bmatrix}
\frac{\partial \tau_{xx}}{\partial x}+\frac{\partial \tau_{yx}}{\partial y}+\frac{\partial \tau_{zx}}{\partial z} \\
\frac{\partial \tau_{xy}}{\partial x}+\frac{\partial \tau_{yy}}{\partial y}+\frac{\partial \tau_{zy}}{\partial z} \\ \frac{\partial \tau_{xz}}{\partial x}+\frac{\partial \tau_{yz}}{\partial y}+\frac{\partial \tau_{zz}}{\partial z}
\end{bmatrix}\)
6. What are the two viscosity coefficients involved in the relationship between stress tensor and strain rate of fluids?
a) Kinematic viscosity and bulk viscosity
b) Dynamic viscosity and kinematic viscosity
c) Dynamic viscosity and bulk viscosity
d) Kinematic viscosity and volume viscosity
View Answer
Explanation: The two viscosities involved in stress train relationship of fluids is dynamic viscosity coefficient and bulk viscosity coefficient. Bulk viscosity coefficient for diagonal elements respectively.
7. What is the relationship between bulk viscosity coefficient (λ) and the dynamic viscosity coefficient (μ)?
a) λ=\(-\frac{2}{3}\) μ
b) λ=\(\frac{2}{3}\) μ
c) λ=\(-\frac{1}{3}\) μ
d) λ=\(-\frac{1}{2}\) μ
View Answer
Explanation: The bulk viscosity coefficient represents fluid compressibility effects. λ=\(-\frac{2}{3}\) μ is the relationship between the bulk viscosity coefficient and the dynamic viscosity coefficient.
8. Express the shear stress tensor(τ) of a three-dimensional fluid flow element in terms of the velocity vector(v).
a) \(\tau=\mu\left\{(\nabla \vec{v})^T\right\}+\lambda(\nabla.\vec{v})I\)
b) \(\tau=\mu\left\{(\nabla \vec{v})\right\}+\lambda(\nabla.\vec{v})I\)
c) \(\tau=\mu\left\{(\nabla \vec{v})^T+(\nabla.\vec{v})^T\right\}\)
d) \(\tau=\mu\left\{(\nabla \vec{v})^T+(\nabla.\vec{v})^T\right\}+\lambda(\nabla.\vec{v})I\)
View Answer
Explanation: The shear stress tensor of a fluid element can be given by \(\tau=\mu\left\{(\nabla \vec{v})^T+(\nabla.\vec{v})^T\right\}+\lambda(\nabla.\vec{v})I\). This is not applicable for practical cases. However, common fluids like air and water are assumed to be Newtonian for using this relationship.
9. Express \(\tau_{yz}\) in terms of velocity gradients.
a) \(\tau_{yz}=μ(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})\)
b) \(\tau_{yz}=μ(\frac{\partial u}{\partial z}+\frac{\partial u}{\partial y})\)
c) \(\tau_{yz}=μ(\frac{\partial v}{\partial x}+\frac{\partial w}{\partial x})\)
d) \(\tau_{yz}=μ(\frac{\partial w}{\partial z}+\frac{\partial v}{\partial y})\)
View Answer
Explanation: For non-diagonal elements,
\(\tau=\mu\left\{∇\vec{v}+(∇\vec{v})^T\right\}\)
\(\tau_{yz}=\mu(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})\).
10. Viscous forces fall into which kind of the following forces acting on a body?
a) Pressure force
b) Tensile force
c) Body forces
d) Surface forces
View Answer
Explanation: The two types of forces acting on a fluid are body forces and surface forces. Body forces are the forces produced by the fluid element itself. Surface forces are the one acting on the fluid elements. Viscous forces act on the element and it comes under surface forces.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Mechanical Engineering MCQs
- Check Chemical Engineering Books
- Apply for Chemical Engineering Internship
- Apply for Mechanical Engineering Internship
- Check Mechanical Engineering Books
