This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Convection-Diffusion Problems – Hybrid Differencing Scheme”.
1. The hybrid differencing scheme is a combination of ____________ and ___________
a) upwind and downwind schemes
b) downwind and central difference schemes
c) central difference and upwind schemes
d) two types of central difference schemes
View Answer
Explanation: Hybrid differencing scheme was introduced by Spalding in 1970s. It is the hybrid between upwind and central differencing schemes so that the advantages of both of these schemes is utilized.
2. The difference scheme to be used in the hybrid system is chosen by evaluating the ____________
a) Local Peclet number
b) Global Peclet number
c) Reynolds number
d) Nusselt number
View Answer
Explanation: The central differencing scheme works well with low Peclet numbers and the upwind scheme works well for high Peclet numbers. So, the differencing scheme to be used in this method is chosen using the Peclet number.
3. The hybrid differencing scheme is ____________
a) never bounded
b) bounded unconditionally
c) bounded in the low Peclet number
d) bounded in the high Peclet number
View Answer
Explanation: The coefficients of the hybrid differencing scheme is always positive. So, it is unconditionally bounded. There is no particular region for the boundedness of the hybrid differencing scheme.
4. What is the order of accuracy of the hybrid differencing scheme?
a) Fourth-order
b) Third-order
c) Second-order
d) First-order
View Answer
Explanation: The major disadvantage of the hybrid difference scheme is its low order of accuracy based on the Taylor series truncation term. It is first-order accurate. Yet, it is useful for solving practical flow problems.
5. Which of these is correct about the hybrid differencing scheme?
a) It is conservative but not transportive
b) It is conservative and transportive
c) It is transportive but not conservative
d) It is neither transportive nor conservative
View Answer
Explanation: The hybrid differencing scheme is fully conservative. It satisfies the transportiveness condition by using upwind scheme for high Peclet numbers. So, the scheme is conservative and transportive as well.
6. What is the advantage of the hybrid differencing scheme compared to the QUICK scheme?
a) Transportiveness
b) Accuracy
c) Stability
d) Conservativeness
View Answer
Explanation: The QUICK scheme also possesses conservativeness and transportiveness. QUICK scheme has a higher order of accuracy. But, it is not stable. Stability is the advantage of the hybrid scheme over this scheme.
7. The Peclet number is calculated at the ____________
a) control volume
b) cell centres
c) vertices
d) faces
View Answer
Explanation: The hybrid differencing scheme uses piecewise formulae based on the Peclet number evaluated at the faces of each control volume. Based on this Peclet number, a scheme is chosen.
8. In which of these ranges is the central differencing scheme used?
a) -2≤Pe≤2
b) -1≤Pe≤1
c) -0.5≤Pe≤0.5
d) -5≤Pe≤5
View Answer
Explanation: The central differencing scheme is valid until the Peclet number reaches a value of two. So, in the hybrid difference scheme, in the range -2≤Pe≤2, the central differencing scheme is used.
9. Consider the following stencil.
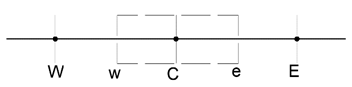
Which is correct about the hybrid differencing scheme?
(Note: q, φ and F are the net flux per unit area, the flow variable and the convective mass flux per unit area respectively).
a) qw=Fw φC if Pe≥2; qw=Fw φC if Pe≤-2
b) qw=Fw φW if Pe≥2; qw=Fw φC if Pe≤-2
c) qw=Fw φW if Pe≥2; qw=Fw φW if Pe≤-2
d) qw=Fw φC if Pe≥2; qw=Fw φW if Pe≤-2
View Answer
Explanation: When the Peclet number goes more than positive two or less than negative two, the upwind scheme is employed. Therefore,
\(q_w = \begin{cases}
F_w \phi_W\, if \, Pe≥2\\
F_w \phi_C\, if \, Pe≤-2\\
\end{cases}\)
10. Consider the following stencil.

For steady two-dimensional convection-diffusion problem, if the general discretized equation is aP φP=aW φW+aE φE+aS φS+aN φN, what is aN using the hybrid differencing scheme?
(Note: ϕ, a, F and D are the flow variable, coefficients, convective mass flux per unit area and diffusion conductance respectively).
a) max(Fn,(Dn–\(\frac{F_n}{2}\)),0)
b) max(-Fn,(Dn+\(\frac{F_n}{2}\)),0)
c) max(-Fn,(Dn–\(\frac{F_n}{2}\)),0)
d) max(Fn,(Dn+\(\frac{F_n}{2}\)),0)
View Answer
Explanation: The coefficients are decided by the Peclet numbers. Put into a simple form, they are given as the maximum among the three as
aN=max(-Fn,(Dn–\(\frac{F_n}{2}\)),0).
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Chemical Engineering Internship
- Check Chemical Engineering Books
- Practice Chemical Engineering MCQs
- Check Mechanical Engineering Books
- Apply for Mechanical Engineering Internship
