This set of Computational Fluid Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Convection-Diffusion Problems – Central Difference Schemes”.
1. Consider the following stencil.
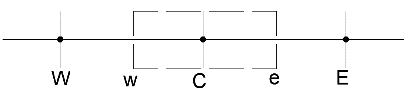
What is Φe as given by the central difference scheme?
(Note: Φ represents the flow variable).
a) \(\phi_E = \phi_c-\frac{(\phi_E+\phi_c)}{(x_E-x_C)}(x_e-x_C)\)
b) \(\phi_E = \phi_c+\frac{(\phi_E+\phi_c)}{(x_E-x_C)}(x_e-x_C)\)
c) \(\phi_E = \phi_c+\frac{(\phi_E-\phi_c)}{(x_E-x_C)}(x_e-x_C)\)
d) \(\phi_E = \phi_c-\frac{(\phi_E-\phi_c)}{(x_E-x_C)}(x_e-x_C)\)
View Answer
Explanation: The central difference scheme incorporates values both behind and ahead of the central node in the equation. Therefore,
\(\phi_E = \phi_c+\frac{(\phi_E-\phi_c)}{(x_E-x_C)}(x_e-x_C)\).
2. Consider the following stencil.

Assume that the grid is a uniform Cartesian grid. What is φw as given by the central difference scheme?
(Note: Φ represents the flow variable).
a) Φc
b) \(\frac{\phi_c+\phi_w}{2}\)
c) \(\frac{\phi_c-\phi_w}{2}\)
d) \(\frac{\phi_w-\phi_c}{2}\)
View Answer
Explanation: The formula for central differencing is
\(\phi_E=\phi_w+\frac{(\phi_c-\phi_w)}{(x_C-x_W)}(x_C-x_w)\)
For uniform grids,
\(\phi_E=\phi_w+\frac{(\phi_c-\phi_w)}{2}(1)\)
\(\phi_E=\frac{(\phi_c+\phi_w)}{2}\).
3. What is the central differencing scheme similar to?
a) Interpolation profile
b) Linear interpolation profile
c) Weighted average method
d) Geometric mean
View Answer
Explanation: The central difference scheme matches the linear interpolation profile. The general form (given below) of both are the same.
Φ=k0+k1(x-xC).
4. What is the relationship between \(\frac{\phi_c-\phi_w}{\phi_E-\phi_w}\) and the Peclet number (Pe) when the grid is uniform?
a) \(\frac{\phi_c-\phi_w}{\phi_E-\phi_w} = \frac{1}{2}(1-\frac{Pe}{2}) \)
b) \(\frac{\phi_c-\phi_w}{\phi_E-\phi_w} = \frac{1}{2}(1+\frac{Pe}{2}) \)
c) \(\frac{\phi_c-\phi_w}{\phi_E-\phi_w} = \frac{1}{2}(\frac{Pe}{2}-1) \)
d) \(\frac{\phi_c-\phi_w}{\phi_E-\phi_w} = (\frac{Pe}{4}) \)
View Answer
Explanation: For the central difference scheme applied to the convection-diffusion problems
\(\frac{\phi_c-\phi_w}{\phi_E-\phi_w}=\frac{a_E}{a_W+a_E}\)
Applying this to
\(\frac{\phi_c-\phi_w}{\phi_E-\phi_w} = \frac{1}{2}(1-\frac{Pe}{2}) \).
5. The central difference approximation goes wrong when _____________
a) Peclet number is negative
b) Peclet number is positive
c) Peclet number is low
d) Peclet number is high
View Answer
Explanation: When the Peclet number is low in the positive or negative direction, the central differencing scheme is valid. If the Peclet number goes beyond a certain value both in the positive and negative direction, this approximation gives unphysical answers.
6. Which of these is correct about the central differencing scheme?
a) The importance of upwind and downwind nodes depends on the problem
b) It gives more importance to the downwind nodes
c) It gives equal importance to upwind and downwind nodes
d) It gives more importance to the upwind nodes
View Answer
Explanation: The central differencing scheme gives equal importance to the upwind and the downwind nodes. The contribution of all the neighbouring nodes is considered for this approximation.
7. The central differencing scheme becomes inconsistent when the Peclet number _____________
a) is higher than 2
b) is less than 2
c) is higher than 5
d) is less than 5
View Answer
Explanation: When the Peclet number goes beyond 2, the central difference approximation fails. The discretization process becomes inconsistent here. In this case, an increase in the neighbouring value will lead to a decrease in the value at the central node.
8. The central difference scheme gives unphysical results when the problem is _____________
a) depends on the boundary conditions
b) equally dominated by diffusion and convection
c) diffusive dominant
d) convective dominant
View Answer
Explanation: In diffusion problems, both the upwind and the downwind neighbours will be equally important. As this is the case in the central differencing scheme, the scheme fits diffusive dominant problems.
9. The order of accuracy of the central differencing scheme is _____________
a) fourth-order
b) third-order
c) second-order
d) first-order
View Answer
Explanation: The central differencing scheme is second-order accurate. This can be proved by using the Taylor series expansion. This is more accurate when compared to the upwind or the downwind schemes.
10. The central differencing scheme gives good results when _____________
a) the grid is coarse
b) the grid is very fine
c) the grid is Cartesian and uniform
d) the gird is on-Cartesian
View Answer
Explanation: The central differencing scheme is good when the cell Peclet number is less than 2. For this, the grid should be very fine. So, the central differencing scheme is good to use when the grid is fine.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Computational Fluid Dynamics Books
- Practice Chemical Engineering MCQs
- Check Chemical Engineering Books
- Apply for Mechanical Engineering Internship
- Check Mechanical Engineering Books
