This set of Computational Fluid Dynamics Puzzles focuses on “Governing Equations – Velocity Divergence”.
1. In mathematical terms, how can the divergence of a velocity vector \((\vec{V})\) be represented?
a) \(\nabla.\vec{V}\)
b) \(\nabla\vec{V}\)
c) \(\nabla \times\vec{V}\)
d) \(\vec{V} \times\nabla\)
View Answer
Explanation: \(\nabla.\vec{V}\)represents the divergence of a vector. \(\nabla\vec{V}\) is gradient which is not possible for a vector. \(\nabla \times\vec{V}\) is the curl of a vector. \(\vec{V} \times\nabla\) does not represent any property.
2. For a control volume moving along with the flow, which of these properties is a constant?
a) Volume
b) Shape
c) Mass
d) Velocity
View Answer
Explanation: Mass of a control volume moving along with the flow will not vary. It is constant with time. The volume, shape and velocity of the control volume may not be the same at all points of time.
3. The time rate of change of a control volume moving along with the flow is represented by substantial derivative. Why?
a) Because the change is substantial
b) Because the change is more
c) Because of control volume
d) Because it is moving with the flow
View Answer
Explanation: As the control volume moves along with the flow, their position coordinates continuously vary with time. This needs a substantial derivative.
4. What is the physical meaning of divergence of velocity?
a) Time rate of change of the volume per unit volume
b) Time rate of change of the volume of a moving fluid element per unit volume
c) Time rate of change of the volume
d) Time rate of change of the volume of a moving fluid element
View Answer
Explanation: Divergence of velocity of a moving fluid model physically means that “time rate of change of the volume of a moving fluid element per unit volume”.
5. Divergence of velocity appears in the governing equations for _____________
a) infinitesimally small elements
b) stationary models
c) moving models
d) finite control volumes
View Answer
Explanation: Divergence of velocity involves the change of volume of the fluid model. For stationary models, volume does not change. So, this applies for only moving fluid elements.
6. Let \((\vec{V} \Delta t).\vec{ds}\) be the change in volume of elemental control volume in time Δt. Over the same time Δt, what is the change in volume of the whole control volume V with control surface S?
a) \(\int(\vec{V}\Delta t).\vec{ds}\)
b) \(\vec{V}\Delta t\)
c) \(\sum(\vec{V}\Delta t).\vec{ds}\)
d) \(\iint_s(\vec{V}\Delta t).\vec{ds}\)
View Answer
Explanation: The change in volume of the whole control volume is the summation of \((\vec{V} \Delta t).\vec{ds}\) over the total control surface S. This summation becomes integral as \(\vec{ds}\) is elemental. Therefore, \(\iint_s(\vec{V}\Delta t).\vec{ds}\) is the total change.
7. Consider a small control volume V with the surface dS with a normal vector \(\vec{n}\). This moves in a fluid flow in time Δt into another position at a velocity \(\vec{V}\) (V in the diagram). What is the change in volume of this small control volume ΔV?
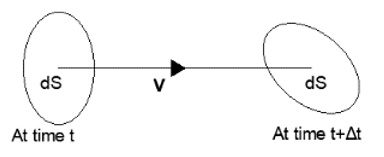
a) \([(\vec{V}\Delta t).\vec{n}]\)
b) \([(\vec{V}\Delta t).\vec{n}]dS\)
c) \([(\vec{V}\Delta t)]dS\)
d) \([(\vec{V}).\vec{n}]dS\)
View Answer
Explanation: The change in control volume can be calculated as the volume of a cylinder with altitude \((\vec{V}\Delta t).\vec{n}\) (product of velocity and time) and base area dS.
8. The time rate of change of volume represented by the following equation corresponds to _________
\(\frac{DV}{Dt}=\iiint_{V}(\nabla.\vec{V})dV\)
Where
V → Control volume
\(\vec{V}\) → Velocity with which the control volume moves.
a) Control volume moving along with the flow
b) Infinitesimal element moving along with the flow
c) Control volume stationary
d) Infinitesimal element stationary
View Answer
Explanation: Stationary models do not have a substantial derivative. If it is not control volume, volume integral is unnecessary. So, the model for this equation is ‘Control volume moving along with the flow’.
9. For infinitesimally small element (with volume δV) moving along with the flow with velocity \(\vec{V}\), which of these equations represent the divergence of velocity?
a) \(\nabla.\vec{V} = \frac{1}{\delta V}\frac{d(\delta V)}{dt} \)
b) \(\nabla.\vec{V} = \frac{D(\delta V)}{dt} \)
c) \(\nabla.\vec{V} = \frac{1}{\delta V}\frac{D(\delta V)}{dt} \)
d) \(\nabla.\vec{V} = \frac{d(\delta V)}{dt} \)
View Answer
Explanation: For control volumes,
\(\frac{DV}{Dt}=\iiint_{V}(\nabla.\vec{V})dV\)
For infinitesimal elements, V can be represented as δ V. Therefore,
\(\frac{D(\delta V)}{Dt}=\iiint_{\delta V}(\nabla.\vec{V})dV\)
As the elements are infinitesimally small, ∇.\(\vec{V}\) is the same for all elements. Hence,
\(\frac{D(\delta V)}{Dt}=(\nabla.\vec{V})\delta V\)
\(\nabla \vec{V}=\frac{1}{\delta V} \frac{D(\delta V)}{Dt}\).
10. Expand divergence of velocity ∇.\(\vec{V}\) for a one-dimensional flow.
a) \(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\)
b) \(\frac{\partial u}{\partial x}\)
c) \(\frac{du}{dx}+\frac{dv}{dy}+\frac{dw}{dz}\)
d) \(\frac{D\vec{V}}{Dt}\)
View Answer
Explanation: Here,
\(\frac{\partial}{\partial x}\vec{i}+\frac{\partial}{\partial y}\vec{j}+\frac{\partial}{\partial z}\vec{k}\)
\(\vec{V}= u\vec{i} +v\vec{j}+w\vec{k}\)
∇.\(\vec{V}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\)
For one-dimensional flow,
∇.\(\vec{V}=\frac{\partial u}{\partial x}\).
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all Puzzles on Computational Fluid Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Chemical Engineering Books
- Apply for Chemical Engineering Internship
- Practice Mechanical Engineering MCQs
- Practice Chemical Engineering MCQs
- Check Mechanical Engineering Books
