This set of Computational Fluid Dynamics Questions and Answers for Campus interviews focuses on “FVM for 1-D Steady State Diffusion”.
1. Which of these statements is true?
a) 1-D steady-state diffusion is the simplest of all transport equations
b) 1-D steady-state diffusion is the toughest of all transport equations
c) 1-D steady-state convection is the simplest of all transport equations
d) 1-D transient diffusion is the simplest of all transport equations
View Answer
Explanation: The one-dimensional steady-state diffusion is the simplest preliminary problem in CFD. This cancels out most of the terms in the general transport equation. In heat flow problems it means conduction and in mass-flow problems, it means diffusion.
2. Which of these equations represent 1-D steady state diffusion?
a) div(Γ grad Φ)+S=0
b) \(\frac{d}{dx}(\Gamma\frac{d\phi}{dx})+S=0\)
c) \(\frac{d\phi}{dt}+\frac{d}{dx}(\Gamma\frac{d\phi}{dx})+S=0\)
d) \(\frac{d\phi}{dt}+div(\Gamma grad\phi)+S=0\)
View Answer
Explanation: The term div(Γ grad Φ) represents diffusion in all three directions. One-dimensional diffusion is given by the equation \(\frac{d}{dx}(\Gamma\frac{d\phi}{dx}.\frac{d\phi}{dt})\) is the transient term. So, this should not be present in the steady-state equation. Considering all these, the correct equation is
\(\frac{d}{dx}(\Gamma\frac{d\phi}{dx}+S)=0\).
3. Which of these theorems is used to transform the general diffusion term into boundary based integral in the FVM?
a) Gauss divergence theorem
b) Stokes’ theorem
c) Kelvin-Stokes theorem
d) Curl theorem
View Answer
Explanation: The general diffusion term is div(Γ gradΦ). Integrating for the finite volume method, it becomes
∫CV div(Γ gradΦ)dV
Applying the Gauss divergence theorem,
∫A\(\vec{n}.\)(Γ gradΦ)dA
This is the boundary based integration as the boundaries will be areas.
4. Which of these gives the statement of one-dimensional steady-state diffusion problem?
a) The diffusive flux of Φ leaving the exit face is the same as the diffusive flux of Φ entering the inlet face
b) The diffusive flux of Φ leaving the exit face plus the diffusive flux of Φ entering the inlet face is equal to the generation of Φ
c) The diffusive flux of Φ leaving the exit face minus the diffusive flux of Φ entering the inlet face is equal to the generation of Φ
d) The diffusive flux of Φ leaving the exit face is the same in magnitude and opposite in direction as the diffusive flux of Φ entering the inlet face
View Answer
Explanation: The diffusive flux of Φ leaving the exit face minus the diffusive flux of Φ entering the inlet face is equal to the generation of Φ. It constitutes the balance equation over the control volume. This ensures conservation.
5. Consider the following stencil.
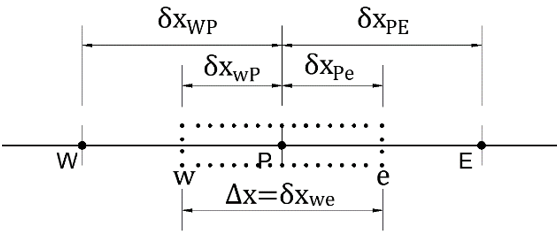
Discretize the diffusive term of the one-dimensional steady-state diffusion problem based on this stencil. (Note: Flow direction is from left to right).
a) \((\Gamma\frac{d\phi}{dx})_e-(\Gamma\frac{d\phi}{dx})_w \)
b) \((\Gamma \frac{d\phi}{dx})_E-(\Gamma\frac{d\phi}{dx})_W\)
c) \((\Gamma A\frac{d\phi}{dx})_E-(\Gamma\frac{d\phi}{dx})_W\)
d) \((\Gamma A\frac{d\phi}{dx})_e-(\Gamma\frac{d\phi}{dx})_w\)
View Answer
Explanation: The diffusive term in one dimension is \(\frac{d}{dx} (\Gamma \frac{d\phi}{dx}).\) Applying integration over the control volume,
\(\int_{\Delta V}\frac{d}{dx}(\Gamma\frac{d\phi}{dx})dV=\int_w^e(\Gamma A\frac{d\phi}{dx})dA=(\Gamma A \frac{d\phi}{dx})_e-(\Gamma A \frac{d\phi}{dx})_w.\)
6. Consider the following stencil.

Apply linear interpolation to the term Γe.
a) \(\frac{\Gamma_e+\Gamma_E}{2}\)
b) \(\frac{\Gamma_W+\Gamma_E}{2}\)
c) \(\frac{\Gamma_P+\Gamma_W}{2}\)
d) \(\frac{\Gamma_P+\Gamma_E}{2}\)
View Answer
Explanation: The value of Γ at the face e can be obtained from the values of Γ at the nodes E and P by linear interpolation.
\(\Gamma_e = \frac{\Gamma_P+\Gamma_E}{2}\)
Similarly,
\(\Gamma_w = \frac{\Gamma_W+\Gamma_P}{2}\).
7. Consider the following stencil.

Get the discretized form of \((\frac{d\phi}{dx})_w\) using the central differencing scheme.
a) \(\frac{\phi_P+\phi_W}{\delta x_{WP}}\)
b) \(\frac{\phi_P-\phi_W}{2}\)
c) \(\frac{\phi_P-\phi_W}{\delta x_WP}\)
d) \(\frac{\phi_P+\phi_W}{2}\)
View Answer
Explanation: To get \((\frac{d\phi}{dx})_i\) using central difference scheme,
\(\frac{d\phi}{dx}_i=\frac{\phi_{i+1}-\phi_{i-1}}{2\Delta x} \)
Applying it to the stencil, i=w, i+1=P, i-1=W and 2Δx=δxWw+δxwP=δxWP. Therefore,
\((\frac{d\phi}{dx})_w=\frac{\phi_P-\phi_W}{\delta x_{WP}}\).
8. The general discretized equation is modified for ____________
a) the central control volume
b) the boundary control volumes
c) the non-boundary control volumes
d) the interior control volumes
View Answer
Explanation: There is special attention needed at the boundary nodes. For control volumes that are adjacent to the domain boundaries, the equation is modified so that the boundary values are incorporated into the equation without any problem.
9. Which of these equations govern the problem of source-free one-dimensional steady-state heat conduction?
a) \(\frac{d}{dx}(k\frac{dT}{dx})\)
b) \(\frac{d}{dx}(k\frac{d\phi}{dx})\)
c) \(\frac{d}{dx}(\Gamma\frac{dT}{dx})\)
d) \(\frac{d}{dx}(\Gamma\frac{d\phi}{dx})\)
View Answer
Explanation: The general one-dimensional steady-state diffusion equation is:
\(\frac{d}{dx}(\frac{\Gamma d\phi}{dx})+S=0 \)
For heat conduction problem, the diffusion constant is the heat conductivity (Γ=k) and the flow variable is temperature (Φ=T). As the given problem is source free, S=0. Therefore, the equation becomes
\(\frac{d}{dx}(k\frac{dT}{dx})=0\).
10. Consider the general discretized equation aPΦP=aWΦW+aEΦE+S. Which of these will become zero for the left boundary node?
a) ΦE
b) aE
c) ΦW
d) aW
View Answer
Explanation: For the left boundary node, there is no western node present. It has only one neighbour on the eastern side. So, the western node coefficient aW is set to zero. ΦW is not zero as we do not know the flow variable at that point and cannot assume.
Sanfoundry Global Education & Learning Series – Computational Fluid Dynamics.
To practice all areas of Computational Fluid Dynamics for Campus Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Computational Fluid Dynamics Books
- Practice Chemical Engineering MCQs
- Practice Mechanical Engineering MCQs
- Apply for Chemical Engineering Internship
- Check Mechanical Engineering Books
