This set of Class 12 Physics Chapter 2 Multiple Choice Questions & Answers (MCQs) focuses on “Combination of Capacitors”.
1. What is the equivalent capacitance when the 2 capacitors are connected in series?
a) Cs = C1 + C2
b) Cs = \(\frac {1}{C_1} + \frac {1}{C_2}\)
c) Cs = C1 + \(\frac {1}{C_2}\)
d) Cs = \(\frac {1}{C_1}\) + C2
View Answer
Explanation: When 2 capacitors are connected in series, the equivalent capacitance Cs is given by
Cs = \(\frac {1}{C_1} + \frac {1}{C_2}\)
When the capacitors are connected in series, the charge passing through each capacitor is the same.
2. Find the equivalent capacitance of the combination shown below.
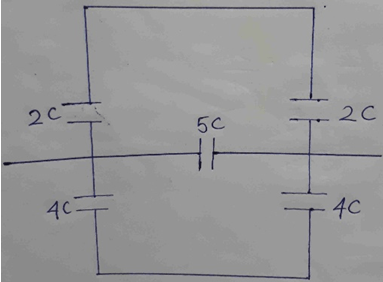
a) 7F
b) 5F
c) 6F
d) 8F
View Answer
Explanation: Both 2 C capacitors are in series. So, equivalent resistance \(\frac {1}{C_s} = \frac {1}{2} + \frac {1}{2}\) = 1F
Both 4 C capacitors are also in series. So, equivalent resistance \(\frac {1}{C_s} = \frac {1}{4} + \frac {1}{4} = \frac {2}{4} = \frac {1}{2}\) → Cs = 2F
Both the above equivalent capacitances are parallel in combination with the 5 C capacitor.
So, Cp = 1 + 2 + 5 = 8 F
Therefore, the equivalent capacitance of the given combination is 8 F.
3. When is the effective capacitance of a capacitor increased?
a) When the capacitors are connected in series
b) When the capacitors are randomly connected
c) When the capacitors are connected in parallel
d) When the capacitors are connected in series and parallel simultaneously
View Answer
Explanation: The effective capacitance of a capacitor is increased when the capacitors are connected in parallel. When the capacitors are connected in parallel, the equivalent capacitance is given by:
Cp = C1 + C2 + C3 +…….
When the capacitors are connected in parallel, the potential difference across each capacitor is the same.
4. True power of a capacitor is 1.
a) True
b) False
View Answer
Explanation: True power is the actual power consumed by the equipment in order to do useful work in an AC circuit. The true power is measured in watts and signifies the power drawn by the circuit’s resistance to do useful work. But, a pure capacitor does not consume or dissipate any true power. So the true power of a capacitor is zero.
5. Three capacitors are connected in the shape of a triangle ABC as shown below. A voltage of 4V is applied between B and C. Calculate the voltage between A and C.
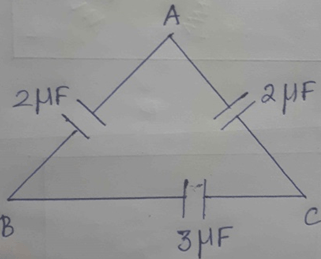
a) 2V
b) 3V
c) 4V
d) 5V
View Answer
Explanation: Both the 2 C capacitors are in series, so, the equivalent capacitance is given by:
\(\frac {1}{C_s} = \frac {1}{2} + \frac {1}{2} = \frac {2}{2}\) = 1μF; Cs = 1μF
Cs is parallel to 3 C capacitor, so overall capacitance is given by:
C = 1 + 3 = 4μF
C = \(\frac {Q}{V}\)
Total charge of the charge (Q) = 4 × 4 = 16μC
QBC = 3 × 4 = 12µC
Q = QBC + QAC
QAC = Q – QBC
QAC = 16 – 12 = 4μC
Therefore voltage between A and C = \(\frac {Q}{C} = \frac {4}{2}\) = 2V
Sanfoundry Global Education & Learning Series – Physics – Class 12.
To practice all chapters and topics of class 12 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 12 - Mathematics MCQs
- Practice Class 12 - Biology MCQs
- Check Class 12 - Physics Books
- Practice Class 11 - Physics MCQs
- Practice Class 12 - Chemistry MCQs
