Series and Parallel - Class 12 Physics MCQ

This set of Class 12 Physics Chapter 3 Multiple Choice Questions & Answers (MCQs) focuses on “Combination of Resistors – Series and Parallel”.

1. In series connection of resistors, what happens to the current across each resistor?
a) Increases
b) Decreases
c) Remain the same
d) Initially increases and then decreases
View Answer

Answer: c
Explanation: When the resistors are connected in series, and current is passed through them, the current passing through each of the resistor is the same. This is because, the resistors are connected end to the end and, therefore, there is only one path for the current to flow through.

2. What is the equivalent resistance of series combination of 3 resistors?
a) R_s = R₁ + R₂ + R₃
b) R_s = \(\frac {1}{(R_1 + R_2 + R_3 )}\)
c) R_s = \(\frac {1}{R_1} + \frac {1}{R_2} + \frac {1}{R_3}\)
d) R_s = \(\frac {(R_1 + R_2)}{R_3}\)
View Answer

Answer: a
Explanation: When three resistors are connected in series, then the equivalent resistance of this combination is R_s = R₁ + R₂ + R₃. So, if 3 resistors having resistances 10, 15, and 20 ohms, are connected in series, then equivalent resistance of this combination is R_s = 10+15+20 = 45 ohms.

3. Identify the combination which is not a series connection.
a) Resistance box
b) Decorative bulbs
c) Fuses
d) Domestic appliances
View Answer

Answer: d
Explanation: Domestic appliances in a house are connected in parallel combinations, and not in series combinations. This arrangement is done so that each of the appliances can switched on and off independently, which is essential in a house’s wiring.

4. The equivalent overall resistance is smaller than the smallest parallel resistor.
a) True
b) False
View Answer

Answer: a
Explanation: Yes, the equivalent overall resistance is smaller than the smallest resistor connected in parallel. This is because, the overall equivalent resistance of parallel combination is: R_p = \(\frac {1}{R_1} + \frac {1}{R_2} + \frac {1}{R_3}\). When the inverse of a resistance value is taken, the value obtained is lesser than the original value. Thus, the sum of inverse values will only provide a lesser value than the initial resistances.

5. Pick out the correct statement from the following about parallel combination of resistors.
a) The current across the resistors are the same
b) The resistance offered by all resistors are the same
c) The potential difference is same across each resistor
d) The equivalent overall resistance is larger than the largest resistor
View Answer

Answer: c
Explanation: In parallel combination, the resistors are connected together at one end, and are also all connected together at the other end. So, the potential difference across the resistors will not change and thus, remains the same.

Sanfoundry Certification Contest of the Month is Live. 100+ Subjects. Participate Now!

6. Calculate resultant resistance between the points A and B in the circuit shown in the figure below.

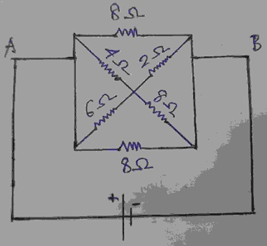
a) 4 ohms
b) 2 ohms
c) 8 ohms
d) 6 ohms
View Answer

Answer: b
Explanation: We can simplify the given diagram as follows:

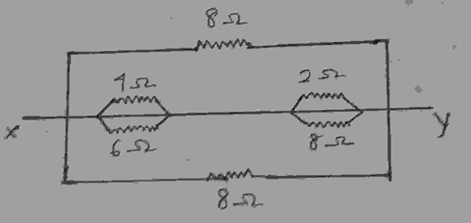
According to the diagram shown above,
\(\frac {1}{R_1} = \frac {1}{4} + \frac {1}{8} = \frac {4 + 6}{4 \times 6} = \frac {10}{24}\) → R₁ = \(\frac {24}{10}\) = 2.4
\(\frac {1}{R_2} = \frac {1}{2} + \frac {1}{8} = \frac {2 + 8}{2 \times 8} = \frac {10}{16}\) → R₂ = \(\frac {16}{10}\)= 1.6
Now, R₁ and R₂ are in series, so, R_s = 2.4 + 1.6 = 4.0.
8 ohms, R_s, and the bottom 8 ohms are in parallel, so, R_p = \(\frac {1}{8} + \frac {1}{4} + \frac {1}{8} = \frac {1}{2}\). Then, when you take the inverse, you will get the equivalent resistance of the given combination, i.e., \(\frac {1}{R_p} = \frac {1}{\frac {1}{2}}\) = 2 ohms.

7. Two wires of the same material have the same length but their radii are in the ratio of 5:3. They are combined in series, where the resistance of the thicker wire is 12 ohms. Calculate the total resistance of the combination.
a) 40
b) 12
c) 32
d) 20
View Answer

Answer: c
Explanation: The given ratio of radii = 5:3; \(\frac {R2}{R1} = \frac {5}{3}\) → R2 = \((\frac {5}{3})\) R1
R1 = 12 ohms (given); R2 = \(( \frac {5}{3} )\) × 12 = 20 ohms. So, R1 = 12 ohms and R2 = 20 ohms
Therefore, total resistance (R) = R1 + R2 (since they are combined in series)
= 12 + 20
= 32 ohms
Thus, the total resistance of the combination is 32 ohms.

8. Three resistors each of 5 ohms are connected in the form of a triangle. What is the resistance between the vertices?
a) \(\frac {3}{10}\)
b) \(\frac {10}{3}\)
c) \(\frac {15}{50}\)
d) \(\frac {2}{5}\)
View Answer

Answer: b
Explanation: Equivalent resistance = 5 + 5 + \(\frac {1}{5}\) (since first two are in series, and they are in parallel to the third in case of a triangular arrangement)
\(\frac {1}{R}\) = 10 + \(\frac {1}{5} = \frac {(5 + 10)}{5 \times 10} = \frac {15}{50} = \frac {3}{10}\)
Thus, R = \(\frac {1}{\frac {3}{10}} = \frac {10}{3}\) ohms
Therefore, the equivalent resistance is \(\frac {10}{3}\) ohms.

9. Two resistors are connected in parallel, whose resistance values are in the ratio 3:1. Find the ratio of power dissipated.
a) 1:3
b) 3:1
c) 1:2
d) 2:1
View Answer

Answer: a
Explanation: We can consider the relation that includes power and resistance, i.e. Power = \(\frac {voltage^2}{resistance}\). Since, the resistors are connected in parallel, the voltage across them will be the same. From this relation, power and resistance are inversely proportional to each other.
Thus, \(\frac {P1}{P2} = \frac {R2}{R1} = \frac {1}{3}\)
So, the power dissipated is in the ratio is 1:3.

10. A set up is such that there are three similar resistors, each of 20 ohms resistance. Two of them are connected in parallel, and this combination is connected in series with the third one. The maximum power that can be consumed by each resistor is 30 W. Then, what is the maximum power that can be consumed by the combination of all three resistors?
a) 30
b) 20
c) 35
d) 45
View Answer

Answer: d
Explanation: The equivalent overall resistance of the parallel combination is:
\(\frac {1}{R1} = \frac {1}{20} + \frac {1}{20} = \frac {2}{20} = \frac {1}{10}\) → R₁ = 10 ohms.
R1 is in series with R2; So, R3 = R1 + R2 = 10 + 20 = 30 ohms.
Now, we can employ the method of cross-multiplication:
For 20 ohms resistor → 30 W power consumed
For 30 ohms resistor combination → x
20x = 30 × 30
x = \(\frac {30 \times 30}{20}\)
x = 45
Therefore, the power consumed by the parallel combination is 45 ohms.

Sanfoundry Global Education & Learning Series – Physics – Class 12.

To practice all chapters and topics of class 12 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Class 12 Physics MCQ – Electrical Energy & Power

» Next - Class 12 Physics MCQ – Current Electricity – Cells, Emf and Internal Resistance

Related Posts:

Recommended Articles: