Moving Coil Galvanometer - Class 12 Physics MCQ

This set of Class 12 Physics Chapter 4 Multiple Choice Questions & Answers (MCQs) focuses on “Moving Coil Galvanometer”.

1. What is moving coil galvanometer used for?
a) Measurement of voltage only
b) Measurement of resistance
c) Measurement of small currents
d) Measurement of electric field
View Answer

Answer: c
Explanation: Moving Coil Galvanometer is an instrument used for the detection and measurement of current. It is sensitive instrument and can measure current even if it is only a few microamperes. It was invented by Johann Schweigger in the 1800s.

2. Pick out the expression for galvanometer constant from the following?
a) G = \(\frac {k}{NAB}\)
b) G = k × NAB
c) G = \(\frac {NAB}{k}\)
d) \(\frac {1}{G} \, = \, \frac {k}{NAB}\)
View Answer

Answer: a
Explanation: In a moving coil galvanometer, the current (I) passing through the galvanometer is directly proportional to its deflection (θ), i.e.
I = Gθ
Where G = \(\frac {k}{NAB}\) ➔ Galvanometer constant
N = number of turns in the coil; A = area of coil; B = strength of the magnetic field; k = torsional constant of the spring that means restoring torque per unit twist.

3. Find the true statement.
a) Ammeter is an instrument used to measure potential difference across any element in a circuit
b) Voltmeter is an instrument used to measure current in a circuit
c) Galvanometer constant is dimensionless
d) Current sensitivity is expressed as the exact reverse of the galvanometer constant
View Answer

Answer: d
Explanation: Current sensitivity is defined as the deflection produced in the galvanometer, when unit current flows through it.
I_S = \(\frac {NAB}{k}\) ………………1
The unit of current sensitivity is rad A^-1 or div A^-1.
From 1, we can understand that current sensitivity is expressed as the exact reverse of galvanometer constant (G = \(\frac {k}{NAB}\)).

4. Voltage sensitivity and current sensitivity are related.
a) True
b) False
View Answer

Answer: a
Explanation: Yes, voltage and current sensitivity are related to each other. Current sensitivity
I_S = \(\frac {NAB}{k}\); Voltage sensitivity = \(\frac {\theta }{V} = \frac {\theta }{IR} = \frac {NAB}{Kr}\)
Therefore, voltage sensitivity ➔ V_S = \((\frac {1}{R})\) x I_S.

5. How is a galvanometer converted into an ammeter?
a) By connecting a high resistance shunt in parallel to the galvanometer
b) By connecting a low resistance shunt in parallel to the galvanometer
c) By connecting a high resistance shunt in series with the galvanometer
d) By connecting a low resistance shunt in series with the galvanometer
View Answer

Answer: b
Explanation: A galvanometer can be converted into an ammeter of given range by connecting suitable low resistance S called shunt in parallel to the given galvanometer, whose value is given by:
S = \( [ \frac {I_g}{(I – I_g)} ] \)G
Where I_g is the current for full scale deflection of galvanometer, I is the current to be measured by the galvanometer and G is the resistance of galvanometer.

Note: Join free Sanfoundry classes at Telegram or Youtube

6. How is galvanometer converted into a voltmeter?
a) By connecting a high resistance multiplier in parallel to the galvanometer
b) By connecting a low resistance multiplier in parallel to the galvanometer
c) By connecting a low resistance multiplier in series with the galvanometer
d) By connecting a high resistance multiplier in series with the galvanometer
View Answer

Answer: d
Explanation: A galvanometer can be converted into voltmeter of given range by connecting a high resistance called multiplier in series with the galvanometer, whose value is given as:
R = \((\frac {V}{I_g})\) – G
Where V is the voltage to be measured, I_g is the current for full scale deflection of galvanometer and G is the resistance of galvanometer.

7. What should be the value of shunt resistance of the ammeter in order to increase its range?
a) S = (n – 1) G
b) S = (n – 1)/G
c) S = \(\frac {G}{(n – 1)}\)
d) S = \(\frac {G}{(n + 1)}\)
View Answer

Answer: c
Explanation: In order to increase the range of an ammeter n times, the value of shunt resistance to be connected in parallel is given by:
S = \(\frac {G}{(n – 1)}\)
In order to increase the range of voltmeter n times, the value of resistance to be connected in series with galvanometer is given by:
R = (n – 1) G

8. An ideal ammeter has infinite resistance and an ideal voltmeter has zero resistance.
a) True
b) False
View Answer

Answer: b
Explanation: An ammeter is a low resistance instrument and it is always connected in series to the circuit. An ideal ammeter has zero resistance. Voltmeter is a high resistance instrument and it is always connected in parallel with the circuit element across which potential difference is to be measured. An ideal voltmeter has infinite resistance.

9. The galvanometer shown below has a resistance (R_G) of 50.00 Ω. Now, this galvanometer is converted to an ammeter with the help of a shunt resistance (r_S) of 0.05 Ω. Calculate the current passing through the galvanometer in both the cases.

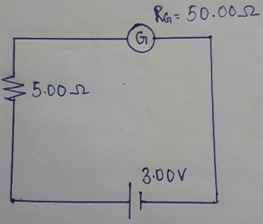
a) 0.0545 A, 0.594 A
b) 0.0545 A, 0.05 A
c) 0.0545 A, 0.06 A
d) 0.07 A, 0.05 A
View Answer

Answer: a
Explanation: R_G = 50.00 Ω; r_S = 0.05 Ω; V = 3.00 V; R = 5.00 Ω
First case ➔ Current (I) = \(\frac {V}{(R_G + R)}\)
= \(\frac {3}{(50 + 5)}\)
= \(\frac {3}{55}\)
= 0.0545 A
Second case ➔ Resistance = \(\frac {(r_S \times R_G)}{(r_S + R_G)}\)
= \(\frac {(0.05 \times 50.00)}{(0.05 + 50.00)}\)
= 0.0499 = 0.05 Ω
Total resistance = 5 + 0.05 = 5.05 Ω
Therefore, current = \(\frac {3}{5.05}\)
= 0.594 A

10. A galvanometer has resistance of 10 ohms and a full scale deflection is produced by 5 milli amperes. What is the value of resistance that should be connected in series with it in order to enable it to read 2V?
a) 20 Ω
b) 10 Ω
c) 40 Ω
d) 30 Ω
View Answer

Answer: d
Explanation: Given: G = 10 Ω; V = 2 V; I_g = 0.05 A
The required equation ➔ I_g = \(\frac {V}{(R + G)}\)
0.05 = \(\frac {2}{(R + 10)}\)
(R + 10) = \(\frac {2}{0.05} = \frac {200}{5}\) = 40
R = 40 – 10
R = 30 Ω

11. When 0.010A current flows through a moving coil galvanometer, it gives full deflection. Then, it is converted into a voltmeter which gives a reading of 10 V using an external resistance of 950 Ω. What is the resistance of the galvanometer (G)?
a) 40 Ω
b) 50 Ω
c) 60 Ω
d) 70 Ω
View Answer

Answer: b
Explanation: Given: V = 10 V; I_g = 0.010A; R = 950 Ω
Required equation ➔ R = \((\frac {V}{I_g})\) – G ➔ G = \((\frac {V}{I_g})\) – R
G = \((\frac {10}{0.010})\) – 950
G = 1000 – 950
G = 50 Ω
Therefore, the resistance of galvanometer is 50 Ω.

12. A moving coil galvanometer has the following characteristics – Number of turns of coil = 50; Area of coil = 70 mm²; Resistance of coil = 30 Ω; Flux density of radial field = 0.1 T; Torsional constant of suspension wire = 7 × 10^-8 N m/rad. Calculate the current and voltage sensitivity.
a) 10 div/mA, 0.166 div/mV
b) 15 div/mA, 0.115 div/mV
c) 5 div/mA, 0.167 div/mV
d) 20 div/mA, 0.100 div/mV
View Answer

Answer: c
Explanation: N = 50; A = 70 mm²; B = 0.1 T; k = 7 × 10^-8 N m/rad; R = 30 Ω
Current sensitivity (I_S) = \(\frac {NAB}{k}\) = 50 × 70 × 10^-6 × \(\frac {0.1}{7}\) × 10^-8
= 350 × \(\frac {100}{7}\) = 5 × 10³ div/amp
= 5 div/mA
Voltage sensitivity (V_S) = \(\frac {NAB}{kR} = \frac {I_S}{R}\)
= \(\frac {5}{30} = \frac {1}{6}\)
= 0.167 div/mV

13. What is the value of the shunt resistance (S) required if a galvanometer has a resistance f 50 Ω and a maximum of 0.05A current that can be passed through it? The ammeter range is changed to 20 A.
a) 0.120 Ω
b) 0.125 Ω
c) 0.130 Ω
d) 0.145 Ω
View Answer

Answer: b
Explanation: Given: I_g = 0.05 A; G = 50 Ω; I = 20 A
Required equation ➔ S = I_g × \(\frac {G}{(I – I_g)}\)
S = \(\frac {0.05 \times 50}{(20 – 0.05)}\)
S = \(\frac {2.5}{19.95}\)
S = 0.125 Ω
Therefore, the required shunt resistance is 0.125 Ω.

14. The current passing through a galvanometer is 30 mA, resistance of the galvanometer is 50 Ω and a shunt is 1 Ω is connected to the galvanometer. What is the maximum current that can be measured by this ammeter?
a) 1.53 A
b) 15.3 A
c) 0.153 A
d) 153 A
View Answer

Answer: a
Explanation: Given: I_g = 30 mA = 0.03 A; S = 1 Ω; G = 50 Ω
Required equation ➔ Maximum current (I) = \( [ \frac {(S + G)}{S} ] \) × I_g
I = \( [ \frac {(50 + 1)}{1} ] \) × 0.03
I = 51 × 0.03
I = 1.53 A

15. In a galvanometer 15% of the total current in the circuit passes through it. If the resistance of the galvanometer is G, then find out the shunt resistance S that is connected to the galvanometer.
a) \(\frac {17G}{3}\)
b) \(\frac {16G}{3}\)
c) \(\frac {5G}{17}\)
d) \(\frac {3G}{17}\)
View Answer

Answer: d
Explanation: I_g = \((\frac {15}{100})\) × I
S = I_g × \(\frac {G}{I – I_g}\)
S = \( ( \frac {15}{100})\) × I × \(\frac {G}{(I – 15 \times \frac {I}{100})}\)
S = [0.15 × \( \frac {I}{(I – 0.15 \times I)} \) ] × G
S = [0.15 × \( \frac {I}{0.85 \times I} \) ] × G
S = \( \frac {15}{85} \) × G
S = \( \frac {3G}{17} \)
Therefore, the shunt resistance required is \( \frac {3G}{17} \).

Sanfoundry Global Education & Learning Series – Physics – Class 12.

To practice all chapters and topics of class 12 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Class 12 Physics MCQ – Torque on Current Loop & Magnetic Dipole

» Next - Class 12 Physics MCQ – Bar Magnet

Related Posts:

Recommended Articles: