This set of Class 12 Physics Chapter 3 Multiple Choice Questions & Answers (MCQs) focuses on “Current Electricity – Temperature Dependence of Resistivity”.
1. Identify the material which is suitable for making standard resistors.
a) Silver
b) Copper
c) Constantan
d) Germanium
View Answer
Explanation: Alloys like constantan or manganin are used for making standard resistance coils due to their high resistivity values and very small temperature coefficient.
2. What is the unit of the temperature coefficient of resistance (α)?
a) oC
b) oC-1
c) \(\frac {\Omega}{ ^{\circ} C}\)
d) \(\frac { ^{\circ} C}{\Omega}\)
View Answer
Explanation: The temperature coefficient of resistivity is defined as the increase in resistivity per unit resistivity per degree rise in temperature.
The unit of the temperature coefficient of resistance is oC-1.
3. Which of the following relation is significant for metals when the temperature increases?
a) Resistivity increases and conductivity decreases
b) Resistivity decreases and conductivity decreases
c) Resistivity and conductivity do not change with temperature
d) Temperature dependence is non-linear
View Answer
Explanation: The resistivity of a metal increases and the conductivity decreases with the increase in temperature. With an increase in temperature, the free electrons collide more frequently with the metal ions. The mean collision time also decreases.
4. Identify the type of material based on the T-ρ graph given below.
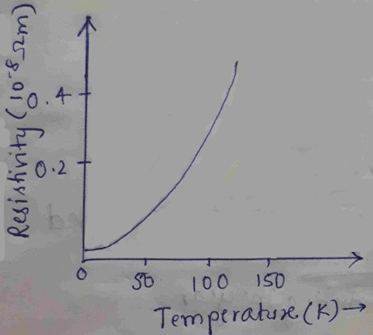
a) Silicon
b) Polymer
c) Nichrome
d) Copper
View Answer
Explanation: For metals, the temperature coefficient of resistivity is positive. At lower temperatures, the resistivity of a pure metal increases as a higher power of temperature. So, the answer is copper, which is a metal.
5. Which among the following has weak temperature dependence values with resistivity?
a) Silver
b) Copper
c) Nichrome
d) Germanium
View Answer
Explanation: Alloys have high resistivity. The resistivity of nichrome has weak temperature dependence. At absolute zero, a pure metal has negligibly small resistivity while an alloy like nichrome has some residual resistivity.
6. The resistivity of semiconductors and insulators decreases linearly with the increase of temperature.
a) True
b) False
View Answer
Explanation: The resistivity of semiconductors and insulators decreases exponentially with the increase in temperature. This is because the number density of free electrons increases exponentially with the increase in temperature.
7. The resistivity of ‘X’ decreases with temperature and its coefficient of resistivity is negative. Identify X.
a) Silver
b) Silicon
c) Copper
d) Nichrome
View Answer
Explanation: The coefficient of resistivity is negative for semiconductors and their resistivity decreases with temperature. The relaxation time does not change with temperature but the number density of free electrons increases exponentially with the increase in temperature. Consequently, the resistivity decreases exponentially with the increase in temperature.
8. A wire has a resistance of 5.5 Ω at 19oC and 21.5 Ω at 200oC. Find the temperature coefficient of resistivity(α) of the material.
a) 0.016 oC-1
b) 0.160 oC-1
c) 1.600 oC-1
d) 16.00 oC-1
View Answer
Explanation: Temperature coefficient α=\(\frac {(R_2-R_1)}{R_2(T_2-T_1)}\).
α = \(\frac {(21.5-5.5)}{(5.5(200-19))}\)
= 0.01607 oC-1.
9. Which of the following is not a valid reason for using alloys to make standard resistors?
a) Alloys have a high value of resistivity
b) They are least affected by air and moisture
c) Alloys have a large temperature coefficient
d) Their contact potential with copper is small
View Answer
Explanation: Alloys have a high value of resistivity. They have a very small temperature coefficient. So their resistance does not change appreciably even for several degrees rise of temperature. That leaves the answer – alloys have a large temperature coefficient.
10. Identify the temperature at which the resistance of copper would be double of its resistance at oC. Given α (temperature coefficient of resistivity) for copper=3.9 x 10-3 oC-1.
a) 125oC
b) 256oC
c) 1080oC
d) 273oC
View Answer
Explanation: α=\(\frac {(R_2-R_1)}{R_2(T_2-T_1)}\).
α=\(\frac {(2R_0-R_0)}{R_0(T-0)} = \frac {1}{T}\).
T=\(\frac {1}{\alpha}\)
= \(\frac {1}{3.9}\) x 10-3 oC-1
= 256oC.
Therefore, the required temperature is 256oC.
Sanfoundry Global Education & Learning Series – Physics – Class 12.
To practice all chapters and topics of class 12 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 12 - Chemistry MCQs
- Check Class 12 - Physics Books
- Practice Class 12 - Biology MCQs
- Practice Class 11 - Physics MCQs
- Practice Class 12 - Mathematics MCQs
