This set of Mechanical Metallurgy Questions and Answers for Freshers focuses on “Elastic Behaviour – Hydrostatic & Deviator Component of Stress – 2”.
1. The 3-dimensional state of stress consists of 3 unequal principal stresses acting on a point, this is called the triaxial state of stress. If two of the three principal stresses are equal, the state of stress is known as __________
a) cylindrical
b) uniaxial
c) spherical/hydrostatic
d) triaxial
View Answer
Explanation: Physically, triaxial state of stress can be considered as 3 dimensions object with length, breadth, and height. If 2 out of 3 dimensions are equal then it represents a cylinder where length and breadth are equal and height is different. Based on this idea, the name is derived as cylindrical state of stress.
2. The three-dimensional state of stress consists of 3 unequal principal stresses acting on a point, this is called the triaxial state of stress. If all the three principal stresses are equal, the state of stress is known as __________
a) cylindrical
b) uniaxial
c) spherical/hydrostatic
d) triaxial
View Answer
Explanation: As all the three stresses are equal, it is the equivalent of a sphere where all the dimension is equal to the radius of the sphere and, that is why the state of stress is known as spherical or hydrostatic.
3. The state of stress in 3-dimension is given by the following determinant, the coefficient of σ2 is an invariant quantity which is equal to ________
\(\begin{vmatrix}\sigma-\sigma x & -\tau yx & -\tau zx\\ -\tau xy & \sigma-\sigma y & -\tau zy\\ -\tau xz & -\tau yz & \sigma-\sigma z\end{vmatrix}\)
a) σx+σy+σz
b) σxσy+σyσz+σzσx-τxy2- τyz2- τzx2
c) σxσyσz+2τxyτyzτzx-σxτxy2 -σyτyz2 -σzτzx2
d) 1
View Answer
Explanation: Solve the determinant. we get expression: σ3-(σx+σy+σz)σ2+(σxσy+σyσz+σzσx-τxy2- τyz2- τzx2) σ+(σxσyσz+2τxyτyzτzx-σxτxy2 -σyτyz2 -σzτzx2)=0
So, the coefficient of σ2 is σx+σy+σz.
4. If Two of the 3 principal stresses are zero, the state of stress is known as __________
a) cylindrical
b) uniaxial
c) spherical/hydrostatic
d) triaxial
View Answer
Explanation: If 2 of the principal stresses are zero that means only in a single direction stress is acting. This is a typical case of tensile testing also known as uniaxial loading.
5. A cubic shape body is subjected to stresses as shown in the figure below. If both are stresses are equal in magnitude, calculate the shear stresses on black and green planes.
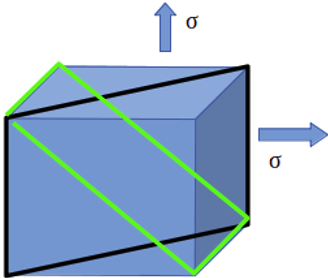
a) Black=σ/2, green=0
b) Black=0, green=σ/2
c) Black=σ/2, green=σ/2
d) Black=σ, green=σ
View Answer
Explanation: The stress of magnitude σ will generate the shear stress of σ/2 on the plane which is at 45 degrees with principal stress direction.
In the case of black plane, stress acting in the right direction will create stress of σ/2 on the plane. The stress acting in the upward direction is parallel to the black plane, so its contribution to shear stress will be zero. So, total shear stress in this black plane is σ/2.
In the case of green plane, stress acting in the right direction will create stress of σ/2 on the green plane; the stress acting in the upward direction also create stress σ/2, but in the opposite direction. So the net result will be zero stress in the green plane.
6. A cubic shape body is subjected to stress as shown in the figure below. Both are stresses are equal in magnitude but opposite in direction. Calculate the shear stresses on black plane and green plane.
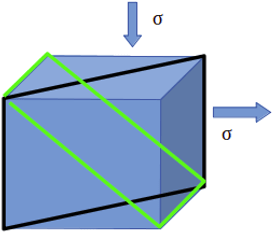
a) Black=σ, green=0
b) Black=σ, green=σ/2
c) Black=σ/2, green=σ/2
d) Black=σ, green=σ
View Answer
Explanation: In the case of black plane, stress acting in the right direction will create stress of σ/2 on the black plane; the stress acting in the upward direction is parallel to the black plane so its contribution in shear stress will be zero. So, total shear stress will σ/2.
In the case of green plane, stress acting in the right direction will create stress of σ/2 on the green plane; the stress acting in the upward direction will also create stress σ/2 in the same direction. So net resultant will be σ/2 + σ/2 = σ.
7. Determine the principal stress for the state of stress?
\(\begin{vmatrix}0 & -100 & 0 \\-100 & 200 & 0 \\ -0 & 0 & -150 \end{vmatrix}\)
a) σ1=100, σ2=200, σ3=-150
b) σ1=-100, σ2=-200, σ3=-150
c) σ1=241.42, σ2=-41.42, σ3=-150
d) σ1=150, σ2=41.42, σ3=-241.42
View Answer
Explanation: There are 2 ways to solve this problem.
The first approach is to use the equation of 3-dimension state stress:
σ3-(σx+σy+σz)σ2+(σxσy+σyσz+σzσx-τxy2- τyz2- τzx2) σ+(σxσyσz+2τxyτyzτzx-σxτxy2 -σyτyz2 -σzτzx2)=0
But this calculation will take a lot of time.
The second approach is to solve using determent.
Rewrite the determine in this form:
\(\begin{vmatrix}\sigma-0 & -100 & 0\\ -100 & \sigma-200 & 0 \\ -0 & 0 & \sigma-(-150)\end{vmatrix}\)
It converts into a cubic equation in term of σ. The 3 solution of equation will be 3 principal stress.
=> σ3-(200-150) σ2+ [(100)(-150)-(-100)2] σ+[(-150)(-100)2]=0
One of the solutions of this cubic equation is –150, because corresponding shear stresses are zero.
Rewriting the equation as:
=> (σ-(-150))*(σ2-200σ-(100)2) = 0.
=> (σ2-200σ-(100)2)= 0
=> σ = 241.42, -41.42.
8. In 2-dimensional state of stress, shear stress maximum (τmax) occurs on a plane halfway between the two principal planes.
a) True
b) False
View Answer
Explanation: Because the components of principal stresses will be maximum at an angle of 45 degrees and summation of 2 principal stresses will add up and give maximum value of shear stress.
9. In the case of pure shear forces, normal stresses develop in all the planes except the planes where shear stresses are maximum.
a) True
b) False
View Answer
Explanation: In case of pure shear, it generates normal stress on a plane with periodically varying angle.
10. In the case of pure normal forces, shear stresses develop in all planes except the planes where normal stresses are maximum.
a) True
b) False
View Answer
Explanation: In this case, all planes feel equal to normal stresses. There is no shear stress on any of the plane. Because shear stress always cancels out.
Sanfoundry Global Education & Learning Series – Mechanical Metallurgy.
To practice all areas of Mechanical Metallurgy for Freshers, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Metallurgical Engineering MCQs
- Check Metallurgical Engineering Books
- Check Mechanical Metallurgy Books
- Apply for Metallurgical Engineering Internship
