This set of Mechanical Metallurgy Multiple Choice Questions & Answers (MCQs) focuses on “Fracture Mechanics – Kic Plane-Stress Toughness Testing”.
1. The geometry of the plastic zone in front of a crack tip is shown in the following figure.
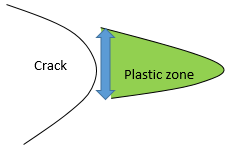
a) True
b) False
View Answer
Explanation: The given diagram represents the state of crack opening correctly. The width of a crack causes the successive displacement of the break and is called the crack opening displacement.
2. The J integral method is used for the _______________ materials.
a) high strength plastic materials
b) low strength ductile material
c) low strength brittle material
d) high strength brittle material
View Answer
Explanation: Most of the crack opening modes work fine with high strength materials, but for the low strength ductile materials it fails to convert to useful results, that is why the J-integral approach is used for such materials.
3. The J integral is the path-dependent method.
a) True
b) False
View Answer
Explanation: The J-integral is an independent path method. It uses the concept of integration of energy per unit of the contour profile of crack.
4. According to the J-Integral, the fracture occurs when the J integral value reaches a critical value. The value of J is equal to____________
a) \(\int(W dy-T \frac{du}{dx} ds)\)
b) \(\int(W dy-T ds)\)
c) \(\int(WT \frac{du}{dx} ds)\)
d) \(\int(W dy+T \frac{du}{dx} ds)\)
View Answer
Explanation: The value of the J integral is given as the
-> \(\int(W dy-T \frac{du}{dx} ds)\)
Where; W is the strain energy per unit volume
T is the outward traction / stress vector acting on the contour around the crack
u is the displacement vector
ds is the increment in the contour path
x, y are the rectangular coordinates
\(T(\frac{du}{dx}) \,ds\) is the rate of the work input from the stress field into the area enclosed
5. The J-Integral is interpreted as the potential energy difference between the two identically loaded sample having slightly different crack lengths. Mathematically it can be written as __________
a) J=dUo/da=K2/E’
b) J=dUo/da=K/E’
c) J=dUo/da=K2/E2
d) J=dUo/da=K/E
View Answer
Explanation: The J-integral approach says that the value of J is equal to strain energy released rate (obtained under elastic condition).
So it is written as J=dUo/da.
6. The value of J integral in potential energy term is written as J=dUo/da=K2/E’. The value of E’ in case of plane stress is equal to ______ (where v is the poison’s ratio).
a) E
b) Ev
c) E/v
d) E2v
View Answer
Explanation: For the plane stress the equation is written as:
J=dUo/da=K2/E’
Where E’=E.
7. If the crack length is doubled than the original value, the potential energy of the J integral will change by a factor of ____
a) 1
b) 2
c) 1/2
d) 4
View Answer
Explanation: The potential energy of J integral is written as:
J=dUo/da=K2/E’;
The constant K2 is defined as πc2σ2; c is crack length,
Hence if the crack length is increased by a factor of 2, the constant K2 will increase by a factor of 4.
So the potential energy will increase 4 factor.
8. For the evaluation of J-integral value from the compact tension specimen, the amount of J in the below-shown sample is equal to __________
Where A = area under the load vs. displacement curve
b=W-a
B=Specimen thickness
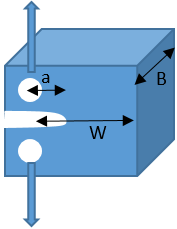
a) J=2A/Bb
b) J=2ABb
c) J=2AB/b
d) J=A2/Bb
View Answer
Explanation: For the three-point bend test having a compact tension specimen, the J integral value is equal to:
J=2A/Bb.
9. The R-curve is used to calculate the _______________ to fracture of the material during slow and stable crack propagation.
a) increment
b) resistance
c) flow
d) toughness
View Answer
Explanation: The concept of R-curve is slightly different from the J-curve idea, where the resistance to fracture of the slow and stable crack is calculated.
10. According to Irwin’s theory of crack resistance, the failure occurs when the rate of change of __________ release rate is equal to the rate of change of _______________ to the crack growth.
a) strain energy, resistance
b) resistance, plastic flow
c) plastic flow, strain energy
d) resistance, plastic flow
View Answer
Explanation: According to Irwin’s theory of crack resistance, the failure occurs when the rate of change of strain energy release rate is equal to the rate of change of resistance to the crack growth.
-> dR/da.
Sanfoundry Global Education & Learning Series – Mechanical Metallurgy.
To practice all areas of Mechanical Metallurgy, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Metallurgical Engineering MCQs
- Apply for Metallurgical Engineering Internship
- Check Metallurgical Engineering Books
- Check Mechanical Metallurgy Books
