This set of Mechanical Metallurgy Interview Questions and Answers focuses on “Elastic Behaviour – Stress Description at a Point”.
1. Hooke’s law is obeyed till _____________ in stress-strain curve.
a) propositional limit point
b) yield point
c) tensile Strength Point
d) failure point
View Answer
Explanation: The stress-strain curve defines the relationship between force and elongation of any material. This curve can be divided into 2 major parts.
First one is the linear part, which starts at the origin and extends up to the propositional limit. In this region, slope of the curve remains linear and constant. The slope of the curve is known as young modulus.
The second part is the non-linear part, which begins after the proportional limit point. The relational ship between stress and strain is non-linear in this region. Simple Hooke’s law will not be enough to define the nature of the curve.
2. How many unknowns are required to establish the state of stress at any given point in 3-dimension?
a) 3
b) 6
c) 9
d) 12
View Answer
Explanation: At any point on the 3-dimensional object, to define the state of stress, it requires 3 principle stress components & 6 shear stress components.
Along x-direction=σx (normal stress), τyx, τzx (shear stress)
Along y-direction=σy (normal stress), τxy, τyz (shear stress)
Along z-direction=σz (normal stress), τxz, τyz (shear stress)
3. Plane stress is defined as ________
a) stress in one principal direction is 0
b) stresses in two principal directions are 0
c) strain in one principal direction is 0
d) strain in two principal directions are 0
View Answer
Explanation: When stress along any one of the principal directions is zero, it is known as plane stress condition. For example, a thin plate loaded in plane of the plate.
When one of the sides of the object is small relative to the other two sides, then there is no stress acting in the direction perpendicular to the surface of the plate.
If strain in one of the principal directions is negligible, it is called plane strain.
4. Which of the following statement is NOT correct?
a) The sum of the normal stresses on two perpendicular planes is an invariant quantity
b) The maximum and minimum values of normal stresses on an oblique plane at point P occurs when the shear stress is zero
c) The maximum and minimum values of the normal stress and the shear stress occurs at an angle 90 degree from each other
d) The variation of shear stress and normal stress occurs is in the form of a sine wave with a period equal to 90 degrees
View Answer
Explanation: Statement: The sum of the normal stresses on two perpendicular planes is an invariant quantity. It is correct.
The sum of any two mutually perpendicular stresses is always equal to the sum of principal stresses on the same plane.
=>σx+σy=σ1+σ2, given that σ1 and σ2 are mutually perpendicular to each other.
Statement: The maximum and minimum values of the normal stresses on an oblique plane at point P occurs when the shear stress is zero. It is correct.
When the shear stress is zero on any plane, all the remaining stresses will add up in the normal component giving the maximum normal stress value.
Statement: The maximum and minimum values of the normal stress and the shear stress occurs at an angle 90 degree from each other. It is correct.
Because after substituting the values in equation of stress at an oblique plane, sine 90 will become zero.
Statement: The variation of shear stress and normal stress occurs is in the form of a sine wave with a period equal to 90 degrees. It is incorrect.
Variation of shear stress and normal stress occurs in the form of sine wave, but with a period equal to 180 degrees.
5. According to the sign convention for shear stress, positive shear stress is shown in diagram _____________
a) 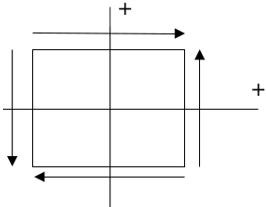
b) 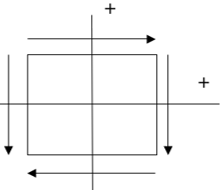
c) 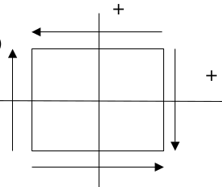
d) 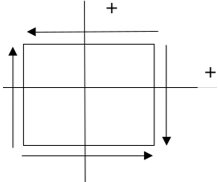
View Answer
Explanation: The condition for positive shear stress is:
– Both the shear stress components of the positive face should point in a positive direction.
– Both the shear stress components of the negative face should point in a negative direction. If both the condition is satisfied, it is pure positive shear stress.
6. A wedge shape body is under stress with principal stresses being σx=25MPa and σy=20MPa. At a certain angle β, the components of stresses are resolved into σ1 & σ2, where both σ1 & σ2 are normal to each other. If the value of σ1=18MPa, find the value of σ2?
a) 25MPa
b) 20MPa
c) 27MPa
d) 18MPa
View Answer
Explanation: By the condition of invariant reaction σx+σy= σ1+σ2.
=> σx=25MPa, σy=20MPa, σ1=18MPa substitute the values in equation
=> 20+25=18+σ2
=> σ2= 45-18=27 MPa.
7. Find the value of shear stress acting on the body, if the principal normal stresses are 70MPa and 60 MPa. The angle of inclination is 30 degrees?
a) 17.32 MPa
b) 2.88 MPa
c) 10 MPa
d) 15 MPa
View Answer
Explanation: Along principal normal stress direction the shear stress will be zero. Using this condition:
=> (tanθ=2τ/(σx-σy))
Substitute the values of principal stresses and θ
=> tan30=2 τ/(70-60)
=> 0.577=2 τ/10
=> τ=2.88 MPA.
8. Transformation of stress along the anticlockwise direction is given by the equation:
σx’= (σx+σy)/2+(σx-σy)/2 cos2θ+τxysin2θ
Given that the principal stresses are 5Y & 9Y and shear stress is Y. If a plane is at 45 degrees anticlockwise from principal plane, find the value of the normal stress?
a) 4Y
b) 5Y
c) 8Y
d) 10Y
View Answer
Explanation: As given in the equation substitute the values of σx=5Y and σy=9Y and θ=45 degree
=> {(5Y+ 9Y)/2}+{(5Y-9Y)/2*cos(2*45)}+Ysin(2*45)
=> 7Y+(-4Y*0)+Y*1 [cos90=0; sin90=1] => 8Y.
9. True stress-strain curve always lies above the engineering stress-strain curve.
a) True
b) False
View Answer
Explanation: True stress calculation considers the instantaneous area of the specimen in the calculation, whereas engineering stress considers the initial area of the specimen in the calculation.
So, as the area is continuously reducing at constant load, the value of true stress keeps on increasing with respect to engineering stress.
10. Bar with cross-sectional area of 0.05m2 is subjected to load of 2000kg, find the stress on the bar in terms of MPa?
a) 392000
b) 40000
c) 0.040
d) 0.392
View Answer
Explanation: Stress is defined as the force per unit area.
Total force on bar=mg; where; m=mass, g=acceleration due to gravity.
=> 2000*9.8=19600N, where g=9.8 m/s2.
Stress=Force/Area
=> 19600/0.05=392000Pa=0.392 MPa.
Sanfoundry Global Education & Learning Series – Mechanical Metallurgy.
To practice all areas of Mechanical Metallurgy for Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Metallurgical Engineering Internship
- Practice Metallurgical Engineering MCQs
- Check Metallurgical Engineering Books
- Check Mechanical Metallurgy Books
